Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Worksheet on Fractions
In worksheet on fractions, all grade students can practice the questions on fractions on a whole number and also on representation of a fraction. This exercise sheet on fractions can be practiced by the students to get more ideas on fractions.
In this worksheet on fractions we will get different types of questions on fractions, comparison of fractions, fractions in ascending order, fractions in descending order, find the fractions to make the fractions equivalent, conversion of fractions, expressed as mixed fractions, express as improper fractions, fractions in lowest terms, reduce to the fractions to the lowest terms and express as a mixed fractions, addition of fractions, subtraction of fractions, multiplication of fractions, division of fractions and word problems on fractions.
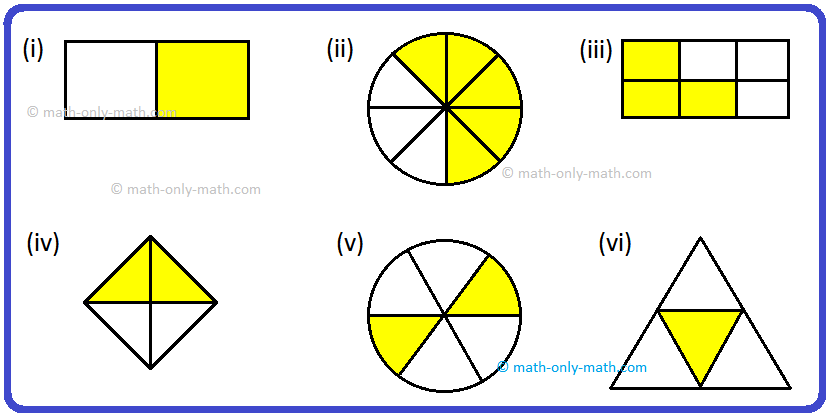
1. Answer the following questions for each given shape:
(a)
(b)
(c)
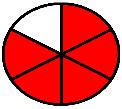
(d)
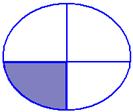
(e)
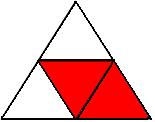
(i) How many equals are there in each shape?
(ii) Express each equal part as a fraction.
(iii) Express the shaded part as a fraction.
(iv) Express each unshaded part as a fraction.
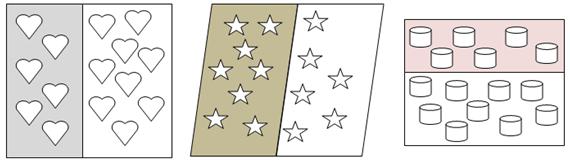
2. Write the fraction for the objects in the shaded part of the closed figure as a part of the whole collection.
3. Write the following fractions in words:
(i) \(\frac{5}{9}\) (five-ninth, five upon nine)
(ii) \(\frac{3}{7}\)
(iii) \(\frac{2}{11}\)
(iv) \(\frac{4}{7}\)
(v) \(\frac{7}{14}\)
(vi) \(\frac{9}{13}\)
(vii) \(\frac{3}{10}\)
4. Fill in the blanks:
(i) For two parts out of seven we say ‘two-seventh’ and write \(\frac{2}{7}\).
(ii) For ‘four parts out of five’ we say ……………… and write ……………….. .
(iii) For ‘nine parts out of seventeen’ we say …………… and write ………….. .
(iv) For ‘three parts out of six’ we say ……………… and write ……………… .
5. Write the fraction representing the coloured parts.
6. Write each of the following as a division.
(i) \(\frac{3}{7}\)
(ii) \(\frac{5}{19}\)
(iii) \(\frac{8}{19}\)
(iv) \(\frac{23}{29}\)
7. Write each of the following as a fraction.
(1) 1 ÷ 9
(ii) 2 ÷ 25
(iii) 3 ÷ 74
(iv) 3 ÷ 91
8. Find \(\frac{3}{9}\) of
(i) 54 m
(ii) 27 kg
(iii) 189 cm
(iv) 72 ml
9. Represent each of the following fractions on the number line.
(i) \(\frac{3}{4}\)
(ii) \(\frac{2}{3}\)
(iii) \(\frac{3}{7}\)
(iv) \(\frac{2}{5}\)
10. Nairitee has 45 pencils. She uses \(\frac{2}{9}\) of them. How many pencils does she have now?
11. What fraction of an ordinary year is 220 days?
12. Look at the number line given in Fig. and answer the following questions:
(i) What fraction does the point A represent?
(ii) What fraction does the point C represent?
(iii) What fraction does the point D represent?
13. Draw pictures to show the following:
(i) five-eighth of a collection
(ii) five-twelfth of a collection
(iii) four-ninth of a rectangular shape
(iv) three-fourth of a square
14. Change into an equivalent fraction with denominator 32.
(i) \(\frac{3}{4}\)
(ii) \(\frac{5}{8}\)
(iii) \(\frac{1}{2}\)
(iv) \(\frac{9}{16}\)
15. Fill in each box with >, < or = to make the statements true:
(i) \(\frac{3}{4}\) □ \(\frac{4}{3}\)
(ii) \(\frac{7}{8}\) □ \(\frac{4}{5}\)
(iii) \(\frac{5}{6}\) □ \(\frac{15}{18}\)
(iv) \(\frac{15}{13}\) □ \(\frac{15}{11}\)
(v) \(\frac{20}{32}\) □ \(\frac{1}{2}\)
(vi) \(\frac{7}{8}\) □ \(\frac{7}{10}\)
(vii) \(\frac{3}{5}\) □ \(\frac{2}{5}\)
(viii) \(\frac{5}{7}\) □ \(\frac{8}{11}\)
(ix) \(\frac{4}{7}\) □ \(\frac{20}{35}\)
(x) \(\frac{5}{9}\) □ \(\frac{12}{27}\)
(xi) \(\frac{2}{3}\) □ \(\frac{3}{4}\)
(xii) \(\frac{3}{6}\) □ \(\frac{3}{18}\)
(xiii) \(\frac{3}{7}\) □ \(\frac{5}{7}\)
(xiv) \(\frac{4}{5}\) □ \(\frac{5}{6}\)
(xv) \(\frac{14}{17}\) □ \(\frac{42}{51}\)
(xvi) \(\frac{1}{10}\) □ \(\frac{3}{20}\)
(xvii) \(\frac{4}{5}\) □ \(\frac{6}{25}\)
(xviii) \(\frac{5}{24}\) □ \(\frac{15}{72}\)
16. Reduce the following fractions into their lowest terms:
or, Express in the lowest terms.
(i) \(\frac{12}{18}\)
(ii) \(\frac{24}{36}\)
(iii) \(\frac{62}{96}\)
(iv) \(\frac{40}{120}\)
(v) \(\frac{40}{56}\)
(vi) \(\frac{3}{9}\)
(vii) \(\frac{4}{14}\)
(viii) \(\frac{10}{80}\)
(ix) \(\frac{40}{60}\)
(x) \(\frac{30}{70}\)
(xi) \(\frac{99}{110}\)
(xii) \(\frac{82}{160}\)
(xiii) \(\frac{40}{48}\)
(xiv) \(\frac{51}{85}\)
(xv) \(\frac{7}{63}\)
17. Add the following fractions:
(i) \(\frac{2}{4}\) + \(\frac{1}{4}\)
(ii) \(\frac{7}{10}\) + \(\frac{3}{10}\)
(iii) \(\frac{1}{4}\) + \(\frac{1}{4}\)
(iv) \(\frac{3}{14}\) + \(\frac{1}{14}\) + \(\frac{4}{14}\)
(v) \(\frac{3}{18}\) + \(\frac{1}{18}\) + \(\frac{7}{18}\)
(vi) \(\frac{6}{30}\) + \(\frac{4}{30}\)
(vii) \(\frac{4}{14}\) + \(\frac{8}{14}\) + \(\frac{2}{14}\)
(viii) \(\frac{8}{15}\) + \(\frac{1}{15}\) + \(\frac{3}{15}\)
18. Subtract the following fractions.
(i) \(\frac{9}{14}\) - \(\frac{4}{14}\)
(ii) \(\frac{5}{30}\) - \(\frac{4}{30}\)
(iii) \(\frac{7}{12}\) - \(\frac{2}{12}\)
(iv) \(\frac{8}{34}\) - \(\frac{5}{34}\)
19. Which of the following are proper fractions?
(i) \(\frac{4}{3}\)
(ii) \(\frac{7}{11}\)
(iii) \(\frac{6}{19}\)
(iv) \(\frac{5}{11}\)
(v) \(\frac{15}{11}\)
(vi) \(\frac{14}{8}\)
(vii) \(\frac{12}{17}\)
(viii) \(\frac{23}{24}\)
(ix) \(\frac{9}{8}\)
(x) \(\frac{6}{2}\)
20. Classify the following fractions as proper or improper or mixed fractions:
(i) \(\frac{15}{10}\)
(ii) \(\frac{2}{9}\)
(iii) 2\(\frac{6}{7}\)
(iv) \(\frac{35}{51}\)
(ν) \(\frac{16}{29}\)
(vi) \(\frac{41}{11}\)
(vii) \(\frac{327}{128}\)
(viii) 4\(\frac{20}{72}\)
21. Which of the following are groups of like fractions?
(i) \(\frac{1}{5}\), \(\frac{2}{5}\), \(\frac{8}{14}\), \(\frac{6}{18}\)
(ii) \(\frac{3}{11}\), \(\frac{2}{11}\), \(\frac{15}{11}\), \(\frac{22}{11}\)
(iii) \(\frac{18}{7}\), \(\frac{13}{7}\), \(\frac{1}{7}\), \(\frac{22}{7}\)
(iv) \(\frac{4}{2}\), \(\frac{10}{21}\), \(\frac{21}{10}\), \(\frac{7}{6}\)
22. Check whether the given fractions are equivalent or not.
(i) \(\frac{3}{5}\), \(\frac{9}{15}\)
(ii) \(\frac{4}{7}\), \(\frac{19}{23}\)
(iii) \(\frac{4}{9}\), \(\frac{41}{42}\)
(iv) \(\frac{7}{12}\), \(\frac{32}{45}\)
(v) \(\frac{3}{11}\), \(\frac{21}{77}\)
(vi) \(\frac{8}{15}\), \(\frac{30}{65}\)
23. Write 🔲 in each of the following by the correct number:
(i) \(\frac{4}{5}\) = \(\frac{8}{🔲}\)
(ii) \(\frac{5}{7}\) = \(\frac{20}{🔲}\)
(iii) \(\frac{1}{6}\) = \(\frac{🔲}{18}\)
(iv) \(\frac{5}{12}\) = \(\frac{15}{🔲}\)
(v) \(\frac{7}{13}\) = \(\frac{🔲}{39}\)
(vi) \(\frac{7}{15}\) = \(\frac{🔲}{60}\)
24. Find the equivalent fraction of:
(i) \(\frac{5}{7}\) having numerator 25
(ii) \(\frac{5}{6}\) having denominator 42
(iii) \(\frac{7}{9}\) having denominator 72
(iv) \(\frac{6}{18}\) having numerator 3
(v) \(\frac{20}{30}\) having numerator 12
(vi) \(\frac{30}{33}\) having denominator 11
25. Convert each of the following mixed fractions into an improper fraction.
or, Express as improper fractions.
(i) 2\(\frac{1}{3}\)
(ii) 4\(\frac{3}{7}\)
(iii) 8\(\frac{4}{17}\)
(iv) 9\(\frac{6}{20}\)
(v) 2\(\frac{3}{5}\)
(vi) 4\(\frac{4}{9}\)
(vii) 3\(\frac{1}{6}\)
(viii) 5\(\frac{6}{7}\)
(ix) 7\(\frac{2}{9}\)
(x) 3\(\frac{5}{7}\)
(xi) 5\(\frac{7}{12}\)
(xii) 5\(\frac{8}{9}\)
(xiii) 2\(\frac{4}{21}\)
(xiv) 8\(\frac{7}{25}\)
26. Convert each of the following improper fractions into a mixed fraction.
or, Express as mixed fraction
(i) \(\frac{13}{7}\)
(ii) \(\frac{28}{7}\)
(iii) \(\frac{105}{7}\)
(iv) \(\frac{347}{12}\)
(v) \(\frac{15}{4}\)
(vi) \(\frac{35}{6}\)
(vii) \(\frac{19}{4}\)
(viii) \(\frac{71}{8}\)
(ix) \(\frac{96}{5}\)
(x) \(\frac{29}{7}\)
(xi) \(\frac{77}{13}\)
(xii) \(\frac{54}{17}\)
(xiii) \(\frac{90}{7}\)
(xiv) \(\frac{20}{9}\)
27. Write the following in ascending order.
(i) 2/7, 8/7, 5/7, 3/7, 1/7
(ii) 7/5, 7/2, 7/4, 7/3, 7/6
(iii) 2/7, 4/9, 1/8, 3/7, 3/8
(iv) 3/5, 2/5, 2/9, 4/4, 1/3
(v) 7/12, 2/10, 3/8, 2/11, 4/9
(vi) 5/12, 5/24, 13/58, 6/7, 3/8
28. Write the following in descending order.
(i) 3/8, 5/8, 1/8, 7/8, 2/8
(ii) 2/9, 1/3, 4/15, 5/12, 5/6
(iii) 4/5, 2/7, 1/5, 6/7, 3/5
(iv) 9/7, 9/5, 9/4, 9/8, 9/2
(v) 1/2, 2/3, 3/4, 1/6, 3/7
(vi) 2/9, 3/4, 1/2, 2/3, 1/4
29. Fill in the boxes to make the fractions equivalent.
(i) \(\frac{3}{5}\) = \(\frac{🔲}{20}\) = \(\frac{30}{🔲}\)
(ii) \(\frac{2}{5}\) = \(\frac{16}{🔲}\) = \(\frac{🔲}{80}\)
(iii) \(\frac{4}{7}\) = \(\frac{🔲}{28}\) = \(\frac{36}{🔲}\)
(iv) \(\frac{3}{4}\) = \(\frac{15}{🔲}\) = \(\frac{🔲}{28}\)
(ν) \(\frac{3}{7}\) = \(\frac{9}{🔲}\) = \(\frac{🔲}{35}\)
(vi) \(\frac{1}{4}\) = \(\frac{3}{🔲}\) = \(\frac{🔲}{24}\)
(vii) \(\frac{4}{🔲}\) = \(\frac{12}{15}\) = \(\frac{20}{🔲}\)
(viii) \(\frac{3}{7}\) = \(\frac{🔲}{42}\) = \(\frac{36}{🔲}\)
30. Reduce to the lowest terms and express each of them as a mixed number.
(i) 88/6
(ii) 78/12
(iii) 25/15
(iv) 24/9
(v) 77/5
(vi) 54/21
(vii) 45/10
(viii) 62/12
(ix) 69/15
(x) 35/14
31. Find the sum of the following fracions.
(i) 4\(\frac{3}{7}\) + 3\(\frac{2}{7}\)
(ii) 1\(\frac{8}{13}\) + 2\(\frac{11}{39}\)
(iii) 1\(\frac{2}{7}\) + \(\frac{5}{14}\) + 1\(\frac{1}{21}\)
(iv) 3\(\frac{1}{5}\) + 2\(\frac{3}{4}\) + 4\(\frac{1}{2}\)
(v) 3\(\frac{2}{3}\) + 4\(\frac{3}{4}\) + 5\(\frac{3}{5}\)
(vi) 2\(\frac{3}{4}\) + 1\(\frac{4}{5}\) + 1\(\frac{3}{5}\)
(vii) 2\(\frac{1}{6}\) + 1\(\frac{1}{14}\) + \(\frac{7}{36}\)
(viii) 3\(\frac{3}{16}\) + 2\(\frac{7}{8}\) + 2\(\frac{3}{4}\)
31. Find the difference of the following fractions.
(i) \(\frac{5}{7}\) - \(\frac{2}{7}\)
(ii) \(\frac{15}{32}\) - \(\frac{7}{16}\)
(iii) \(\frac{4}{9}\) - \(\frac{2}{27}\)
(iv) \(\frac{3}{8}\) - \(\frac{1}{16}\)
(v) \(\frac{3}{4}\) - \(\frac{2}{3}\)
(vi) 2\(\frac{3}{4}\) - 1\(\frac{5}{8}\)
(vii) 1\(\frac{3}{16}\) - \(\frac{3}{4}\)
(viii) 16\(\frac{3}{4}\) - 9\(\frac{9}{16}\)
(ix) 5\(\frac{6}{7}\) - 3\(\frac{2}{9}\)
(x) 4\(\frac{5}{8}\) - 2\(\frac{19}{24}\)
(xi) 4\(\frac{2}{3}\) - 3\(\frac{2}{5}\)
(xii) 5\(\frac{2}{7}\) - 2\(\frac{5}{21}\)
(xiii) 8\(\frac{3}{4}\) - 4\(\frac{1}{6}\)
(xiv) 7\(\frac{1}{10}\) - 5\(\frac{3}{20}\)
(xv) 9\(\frac{4}{9}\) - 7\(\frac{2}{27}\)
32. Find the product of the following fractions:
(i) \(\frac{4}{7}\) × 9
(ii) \(\frac{6}{17}\) × 12
(iii) \(\frac{9}{28}\) × 12
(iv) 1\(\frac{3}{8}\) × 4
(v) 2\(\frac{5}{9}\) × 15
(vi) 6\(\frac{3}{17}\) × 51
(vii) 2\(\frac{5}{9}\) × \(\frac{2}{3}\)
(viii) 3\(\frac{1}{7}\) × \(\frac{2}{17}\)
(ix) 4\(\frac{3}{8}\) × \(\frac{1}{4}\)
(x) 1\(\frac{1}{4}\) × 2\(\frac{3}{5}\)
(xi) 4\(\frac{3}{8}\) × 2\(\frac{1}{15}\)
(xii) 9\(\frac{3}{7}\) × 2\(\frac{6}{17}\)
(xiii) 5\(\frac{3}{4}\) × 3\(\frac{1}{5}\)
(xiv) 3\(\frac{9}{10}\) × 1\(\frac{3}{11}\)
(xv) 6\(\frac{5}{6}\) × 4\(\frac{1}{3}\)
33. Divide the following fractions:
(i) \(\frac{2}{5}\) ÷ 9
(ii) \(\frac{4}{7}\) ÷ 12
(iii) \(\frac{1}{4}\) ÷ 12
(iv) \(\frac{1}{7}\) ÷ \(\frac{3}{8}\)
(v) \(\frac{2}{17}\) ÷ \(\frac{5}{17}\)
(vi) \(\frac{3}{22}\) ÷ \(\frac{6}{11}\)
(vii) 1\(\frac{5}{8}\) ÷ \(\frac{1}{2}\)
(viii) 4\(\frac{3}{5}\) ÷ \(\frac{1}{7}\)
(ix) 5\(\frac{4}{7}\) ÷ \(\frac{3}{8}\)
(x) 2\(\frac{6}{7}\) ÷ 1\(\frac{6}{17}\)
(xi) 2\(\frac{1}{17}\) ÷ 1\(\frac{3}{34}\)
(xii) 8\(\frac{3}{8}\) ÷ 2\(\frac{2}{7}\)
(xiii) 5\(\frac{1}{2}\) ÷ 4\(\frac{1}{3}\)
(xiv) 7\(\frac{2}{3}\) ÷ 1\(\frac{6}{7}\)
(xv) 6\(\frac{3}{8}\) ÷ 2\(\frac{3}{4}\)
(xvi) 5\(\frac{2}{5}\) ÷ 3\(\frac{2}{15}\)
(xvii) 25\(\frac{1}{6}\) ÷ 5\(\frac{5}{12}\)
(xviii) 6\(\frac{2}{7}\) ÷ \(\frac{3}{5}\)
(xix) 2\(\frac{6}{7}\) ÷ 3\(\frac{1}{24}\)
(xx) \(\frac{6}{17}\) ÷ 1\(\frac{1}{51}\)
(xxi) \(\frac{3}{22}\) ÷ 1\(\frac{23}{25}\)
Worksheet on Fractions Answers:
3. (ii) three-seventh, three upon seven
(iii) two-eleventh, two upon eleven
(iv) four-seventh, four upon seven
(v) seven-fourteenth, seven upon fourteen
(vi) nine-thirteenth, nine upon thirteen
(vii) three-tenth, three upon ten
4. (ii) four-fifth, \(\frac{4}{5}\)
(iii) nine-seventeenth, \(\frac{9}{17}\)
(iv) three-sixth, \(\frac{3}{6}\)
5. (i) \(\frac{1}{2}\)
(ii) \(\frac{5}{8}\)
(iii) \(\frac{3}{6}\)
(iv) \(\frac{2}{4}\)
(v) \(\frac{2}{6}\)
(vi) \(\frac{1}{4}\)
6. (i) 3 ÷ 7
(ii) 5 ÷ 19
(iii) 8 ÷ 19
(iv) 23 ÷ 29
7. (i) \(\frac{1}{9}\)
(ii) \(\frac{2}{25}\)
(iii) \(\frac{3}{74}\)
(iv) \(\frac{3}{91}\)
8. (i) 18 m
(ii) 9 kg
(iii) 63 cm
(iv) 24 ml
9.
10. 35 pencils
11. \(\frac{220}{365}\)
12. (i) A represents as \(\frac{1}{12}\)
(ii) C represents as \(\frac{7}{12}\)
(iii) D represents as \(\frac{9}{12}\)
13.
14. (i) \(\frac{24}{32}\)
(ii) \(\frac{20}{32}\)
(iii) \(\frac{16}{32}\)
(iv) \(\frac{18}{32}\)
15. (i) <
(ii) <
(iii) =
(iv) <
(v) <
(vi) >
(vii) >
(viii) <
(ix) =
(x) >
(xi) <
(xii) >
(xiii) <
(xiv) <
(xv) =
(xvi) <
(xvii) >
(xviii) =
16. (i) \(\frac{2}{3}\)
(ii) \(\frac{2}{3}\)
(iii) \(\frac{31}{48}\)
(iv) \(\frac{1}{3}\)
(v) \(\frac{5}{7}\)
(vi) \(\frac{1}{3}\)
(vii) \(\frac{2}{7}\)
(viii) \(\frac{10}{80}\)
(ix) \(\frac{1}{8}\)
(x) \(\frac{3}{7}\)
(xi) \(\frac{9}{10}\)
(xii) \(\frac{41}{80}\)
(xiii) \(\frac{5}{6}\)
(xiv) \(\frac{3}{5}\)
(xv) \(\frac{1}{9}\)
17. (i) \(\frac{3}{4}\)
(ii) \(\frac{10}{10}\) = 1
(iii) \(\frac{2}{4}\) = \(\frac{1}{2}\)
(iv) \(\frac{8}{14}\) = \(\frac{4}{7}\)
(v) \(\frac{11}{18}\)
(vi) \(\frac{10}{30}\) = \(\frac{1}{3}\)
(vii) \(\frac{14}{14}\) = 1
(viii) \(\frac{12}{15}\) = \(\frac{4}{5}\)
18. (i) \(\frac{5}{14}\)
(ii) \(\frac{1}{30}\)
(iii) \(\frac{5}{12}\)
(iv) \(\frac{3}{34}\)
19. (ii), (iii), (iv), (vii), (viii) are proper fractions because numerators are less than the denominators.
20. (i) improper fraction
(ii) proper fraction
(iii) mixed fraction
(iv) proper fraction
(ν) proper fraction
(vi) improper fraction
(vii) improper fraction
(viii) mixed fraction
21. (ii) and (iii) are like fractions.
22. (i) equivalent fraction
(ii) not equivalent fraction
(iii) not equivalent fraction
(iv) not equivalent fraction
(v) equivalent fraction
(vi) not equivalent fraction
23. (i) 10
(ii) 28
(iii) 3
(iv) 36
(v) 21
(vi) 28
24. (i) \(\frac{25}{35}\)
(ii) \(\frac{35}{42}\)
(iii) \(\frac{56}{72}\)
(iv) \(\frac{3}{9}\)
(v) \(\frac{12}{18}\)
(vi) \(\frac{10}{11}\)
25. (i) \(\frac{7}{3}\)
(ii) \(\frac{31}{7}\)
(iii) \(\frac{140}{17}\)
(iv) \(\frac{186}{20}\)
(v) \(\frac{13}{5}\)
(vi) \(\frac{40}{9}\)
(vii) \(\frac{19}{6}\)
(viii) \(\frac{41}{7}\)
(ix) \(\frac{65}{9}\)
(x) \(\frac{26}{7}\)
(xi) \(\frac{67}{12}\)
(xii) \(\frac{53}{9}\)
(xiii) \(\frac{46}{21}\)
(xiv) \(\frac{207}{25}\)
26. (i) 1\(\frac{6}{7}\)
(ii) 4
(iii) 15
(iv) 28\(\frac{11}{12}\)
(v) 3\(\frac{3}{4}\)
(vi) 5\(\frac{5}{6}\)
(vii) 4\(\frac{3}{4}\)
(viii) 8\(\frac{7}{8}\)
(ix) 19\(\frac{1}{5}\)
(x) 4\(\frac{1}{7}\)
(xi) 5\(\frac{12}{13}\)
(xii) 3\(\frac{3}{17}\)
(xiii) 12\(\frac{6}{7}\)
(xiv) 2\(\frac{2}{9}\)
27. (i) 1/7, 2/7, 3/7, 3/7, 5/7, 8/7
(ii) 7/6, 7/5, 7/4, 7/3, 7/2
(iii) 1/8, 2/7, 3/8, 3/7, 4/9
(iv) 2/9, 1/3, 2/5, 3/5, 4/4
(v) 2/11, 2/10, 3/8, 4/9, 7/12
(vi) 5/24, 13/58, 3/8, 5/12, 6/7
28. (i) 7/8, 5/8, 3/8, 2/8, 1/8
(ii) 5/6, 5/12, 1/3, 4/15, 2/9
(iii) 6/7, 4/5, 3/5, 2/7, 1/5
(iv) 9/2, 9/4, 9/5, 9/7, 9/8
(v) 3/4, 2/3, 1/2, 3/7, 1/6
(vi) 3/4, 2/3, 1/2, 1/4, 2/9
29. (i) 12, 50
(ii) 40, 32
(iii) 16, 63
(iv) 20, 21
(ν) 21, 15
(vi) 12, 6
(vii) 5, 25
(viii) 18, 84
30. (i) 14\(\frac{2}{3}\)
(ii) 6\(\frac{1}{2}\)
(iii) 1\(\frac{2}{3}\)
(iv) 2\(\frac{2}{3}\)
(v) 15\(\frac{2}{5}\)
(vi) 2\(\frac{4}{7}\)
(vii) 4\(\frac{1}{2}\)
(viii) 5\(\frac{1}{6}\)
(ix) 4\(\frac{3}{5}\)
(x) 2\(\frac{1}{2}\)
31. (i) 7\(\frac{5}{7}\)
(ii) 3\(\frac{35}{39}\)
(iii) 2\(\frac{29}{42}\)
(iv) 10\(\frac{9}{20}\)
(v) 14\(\frac{1}{60}\)
(vi) 6\(\frac{3}{20}\)
(vii) 3\(\frac{109}{252}\)
(viii) 8\(\frac{13}{16}\)
31. (i) \(\frac{3}{7}\)
(ii) \(\frac{1}{32}\)
(iii) \(\frac{10}{27}\)
(iv) \(\frac{5}{16}\)
(v) \(\frac{1}{12}\)
(vi) 1\(\frac{1}{8}\)
(vii) \(\frac{7}{16}\)
(viii) 7\(\frac{3}{16}\)
(ix) 2\(\frac{40}{63}\)
(x) 1\(\frac{5}{6}\)
(xi) 1\(\frac{4}{15}\)
(xii) 3\(\frac{1}{21}\)
(xiii) 4\(\frac{7}{12}\)
(xiv) 1\(\frac{19}{20}\)
(xv) 2\(\frac{10}{27}\)
32. (i) 5\(\frac{1}{7}\)
(ii) 4\(\frac{4}{17}\)
(iii) 3\(\frac{6}{7}\)
(iv) 5\(\frac{1}{2}\)
(v) 38\(\frac{1}{3}\)
(vi) 315
(vii) 1\(\frac{19}{27}\)
(viii) \(\frac{44}{119}\)
(ix) 1\(\frac{3}{32}\)
(x) 3\(\frac{1}{4}\)
(xi) 9\(\frac{1}{24}\)
(xii) 22\(\frac{22}{119}\)
(xiii) 18\(\frac{2}{5}\)
(xiv) 4\(\frac{53}{55}\)
(xv) 29\(\frac{11}{18}\)
33. (i) \(\frac{2}{45}\)
(ii) \(\frac{1}{21}\)
(iii) \(\frac{1}{48}\)
(iv) \(\frac{8}{21}\)
(v) \(\frac{2}{5}\)
(vi) \(\frac{1}{4}\)
(vii) 3\(\frac{1}{4}\)
(viii) 32\(\frac{1}{5}\)
(ix) 14\(\frac{6}{7}\)
(x) 2\(\frac{18}{161}\)
(xi) 1\(\frac{33}{37}\)
(xii) 3\(\frac{85}{128}\)
(xiii) 1\(\frac{7}{26}\)
(xiv) 4\(\frac{5}{39}\)
(xv) 2\(\frac{7}{22}\)
(xvi) 1\(\frac{34}{47}\)
(xvii) 4\(\frac{42}{65}\)
(xviii) 10\(\frac{11}{21}\)
(xix) \(\frac{480}{511}\)
(xx) \(\frac{9}{26}\)
(xxi) \(\frac{25}{352}\)
If students have any queries regarding the Worksheet on expanded form of a number questions please fill-up the comment box so that we can help you.
However, suggestions for further improvement, from all quarters would be greatly appreciated.
● Fractional Numbers - worksheets
Worksheet on Equivalent Fractions.
Worksheet on Comparison of Like Fractions.
Worksheet on Conversion of Fractions.
Worksheet on Changing Fractions.
Worksheet on Types of Fractions.
Worksheet on Reducing Fraction.
Worksheet on Addition of Fractions having the Same Denominator.
Worksheet on Subtraction of Fractions having the Same Denominator.
Worksheet on Add and Subtract Fractions.
Worksheet on Fractional Numbers.
From Worksheet on Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
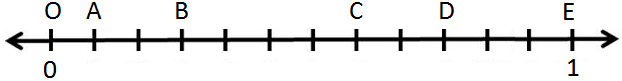

![To convert a percentage into a fraction, place the given number over 100 and reduce it to its lowest term. Consider the following example: (i) 20% [We know % = 1/100]](/image-thumbnails/convert-a-percentage-into-a-fraction.png/default.webp)













New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.