5th Grade Fractions

In 5th Grade Fractions we will discuss about definition of fraction, concept of fractions and different types of examples on fractions.

A fraction is a number representing a part of a whole. The whole may be a single object or a group of objects.

Definition of Fraction: A number that compares part of an object or set with the whole, especially the quotient of two whole numbers, written in the form of \(\frac{x}{y}\) is called a fraction.

The fraction \(\frac{2}{5}\), which means 2 divided by 5, can be represented as 2 books out of a box of 5 books.

A fraction is a

(i) part of a whole

(ii) part of a collection

Concept of 5th Grade Fractions:

A fraction is a number which represents/indicates a part or parts of a whole. Fractions can be represented in three ways:

(i) Fraction as a Part of a Whole:

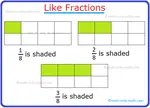
In the given figure, the coloured parts represent \(\frac{5}{8}\) of the whole,

i.e., \(\frac{5}{8}\) 5 indicates 5 parts out of 8 equal parts of a whole. 

So, \(\frac{5}{8}\) is a fraction.

            5  →    Numerator 
            8  →  Denominator

Clearly, a fraction comprises two numbers separated by a horizontal line. The number above the horizontal line is called the numerator and the number below the horizontal line is called the denominator of the fraction.

(ii) Fraction as a Part of a Collection:

We can find the fractional part of a collection by dividing the collection into subgroups equal to the number representing the denominator of the fraction. Then, we take the number of subgroups equal to the number representing the numerator of the fraction.

Consider a collection of 9 balls. If we divide this collection into three equal parts, we get 3 balls in each of the three parts.

Thus, one-third of 9 is 3.

i.e., \(\frac{1}{3}\) of 9 = 9 × \(\frac{1}{3}\) = \(\frac{9}{3}\) = 3

(iii) Fraction as Division:

A fraction can be expressed as a division. Conversely, division can be expressed as fraction.

If 42 pencils are distributed equally among 7 students then each student will get 42 ÷ 7 = 6 pencils.

But if 1 mango is to be distributed among 4 students, then how many mango will a student get?

Obviously, each student gets 1 ÷ 4 i.e., \(\frac{1}{4}\) mango.

Following are Some Examples of 5th Grade Fractions:

(i) Consider the fraction \(\frac{7}{12}\). This fraction is read as ”seven-twelfth” which means that 7 parts out of 12 equal parts in which the whole is divided. In the fraction \(\frac{7}{12}\), 7 is called the numerator and 12 is called the denominator.

(ii) The fraction \(\frac{5}{7}\) is read as ”five-seventh” which means that 5 parts out of 7 equal parts in which the whole is divided. In the fraction \(\frac{5}{7}\), 5 is called the numerator and 7 is called the denominator.

(iii) The fraction \(\frac{3}{10}\) is read as ”three-tenth” which means that 3 parts out of 10 equal parts in which the whole is divided. In the fraction \(\frac{3}{10}\), 3 is called the numerator and 10 is called the denominator.

(iv) The fraction \(\frac{1}{5}\) is read as ”one-fifth” which means that 1 parts out of 5 equal parts in which the whole is divided. In the fraction \(\frac{1}{5}\), 1 is called the numerator and 5 is called the denominator.

For example on 5th Grade Fractions:

1. Mrs. Brown has 24 apples. She ate \(\frac{1}{4}\) of them.

(i) How many apples does she eat?

(ii) How many does she have left?

Solution:

(i) Here the fraction \(\frac{1}{4}\) means take 1 part from 4 equal parts.

So, arrange 24 apples in four equal groups.

Clearly, each group will contain 24 ÷ 4 = 6 apples.

Thus, \(\frac{1}{4}\) of 24 is 6.

Hence, Mrs. Brown ate 6 apples.

(ii) Number of left out apples = 24 – 6 = 18.

2. Andrea has a packet of 20 biscuits. She gives \(\frac{1}{2}\) of them to Andy and \(\frac{1}{4}\) of them to Sally. The rest she keeps.

(i) How many biscuits does Andy get?

(ii) How many biscuits does Sally get?

(iii) How many biscuits does Andrea keep?

Solution:

(i) Here, \(\frac{1}{2}\) of 20 means take 1 part from two equal parts.

So, we arrange 20 biscuits in two equal parts.

Clearly, each part will contain 20 ÷ 2 = 10 biscuits.

Therefore, \(\frac{1}{2}\) of 20 is 10.

Hence, Andy gets 10 biscuits.

(ii) \(\frac{1}{4}\) of 20 means take 1 part from four equal parts.

So, we arrange 20 biscuits in four equal parts.

Clearly, each part will contain 20 ÷ 4 = 5 biscuits.

Therefore, \(\frac{1}{4}\) of 20 is 5.

Hence, Sally gets 5 biscuits.

(iii) Clearly, left out biscuits are kept by Andrea.

Therefore, Andrea keeps 20 – 10 – 5 = 5 biscuits.

5th Grade Fractions

3. What fraction of a day is 8 hours?

Solution:

We have,

One day = 12 hours.

Therefore, 8 hours = \(\frac{8}{12}\) of a day.

Hence, 8 hours is \(\frac{8}{12}\) part of a day.

4. Determine \(\frac{2}{3}\) of a collection of 9 balls.

Solution:

In order to find \(\frac{2}{3}\) of a collection of 9 balls, we divide the collection of 9 balls in 3 equal parts and take 2 such parts. Clearly, each row has \(\frac{9}{3}\) = 3 balls.

When, we take 2 rows out of 3 rows. It represents \(\frac{2}{3}\) of 9 balls. There are 6 balls in 2 rows.

Hence, \(\frac{2}{3}\) of 9 balls = 6 balls.

● Fraction

Representations of Fractions on a Number Line

Fraction as Division

Types of Fractions

Conversion of Mixed Fractions into Improper Fractions

Conversion of Improper Fractions into Mixed Fractions

Equivalent Fractions

Interesting Fact about Equivalent Fractions

Fractions in Lowest Terms

Like and Unlike Fractions

Comparing Like Fractions

Comparing Unlike Fractions

Addition and Subtraction of Like Fractions

Addition and Subtraction of Unlike Fractions

Inserting a Fraction between Two Given Fractions

Numbers Page

6th Grade Page

From 5th Grade Fractions to HOME PAGE