Formation of Numbers
In formation of numbers we will learn the numbers having different numbers of digits.
We know that:
(i) Greatest number of one digit = 9,
Smallest number of 2 digits = 10.
(If one is added to 9, we get 9 + 1 = 10).
(ii) Greatest number of 2 digits = 99,
Smallest number of 3 digits = 100.
(If one is added to 99, we get 99 + 1 = 100).
(iii) Greatest number of 3 digits = 999,
Smallest number of 4 digits = 1000.
(If one is added to 999, we get 999 + 1 = 1000).
(iv) Greatest number of 4 digits = 9999,
Smallest number of 5 digits = 10000.
(If one is added to 9999, we get 9999 + 1 = 10000).
(iv) Greatest number of 5 digits = 99999,
Smallest number of 6 digits = 100000.
(If one is added to 99999, we get 99999 + 1 = 100000).
Thus, if 1 is added to 9 (greatest 1-digit number), we get 10 (smallest 2-digit number).
If 1 is added to 99 (greatest 2-digit number), we get 100 (smallest 3-digit number).
If 1 is added to 999 (greatest 3-digit number), we get 1000 (smallest 4-digit number).
If 1 is added to 9999 (greatest 4-digit number), we get 10000 (smallest 5-digit number).
If we add 1 to 99999, we get 99999 + 1 = 100000, the smallest 6-digit numbers.
|
Number of Digits |
Smallest Number |
Greatest Number |
|
One |
0 |
9 |
|
Two |
10 = 9 + 1 |
99 |
|
Three |
100 = 99 + 1 |
999 |
|
Four |
1000 = 999 + 1 |
9999 |
We observe that
● The smallest 2-digit number is the
(Greatest 1-digit number + 1)
● The smallest 3-digit number is the
(Greatest 2-digit number + 1)
● The smallest 4-digit number is the
(Greatest 3-digit number + 1)
● Therefore,
The smallest 5-digit number is the
(Greatest 4-digit number + 1)
i.e., 999 + 1 = 10000 (Ten thousand)
We read 100000 as one lakh. The sixth place from the right is called lakhs place.
For Example:
500000 --> read as five lakh.
639043 --> read as six lakh thirty-nine thousand forty-three.
832519 --> read as eight lakh thirty-two thousand five hundred nineteen.
999999 --> read as nine lakh ninety-nine thousand nine hundred ninety-nine.
999999 is the greatest 6-digit number.
Look at the following table:
Now we will learn how to use an abacus in number formation
These facts can be expressed on a spike-abacus as follows:
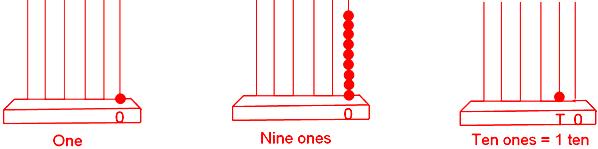
One → 9, 9 + 1 = 10 = One ten
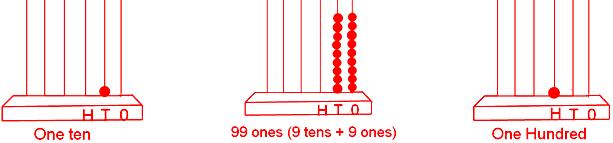
10 → 99, 99 + 1 = 100 = One hundred
100 → 999, 999 + 1 = 1000 = One thousand
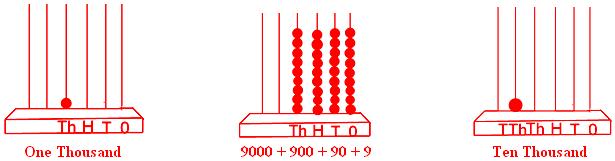
1000 → 9999, 9999 + 1 = 10000 = Ten thousand
1-digit numbers:
1, 2, 3, 4, 5, 6, 7, 8, 9.
2-digit numbers:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, …………., 29,
30, 31, ……., 39, 40, 41,……….., 49, 50, 51,………, 60, 61,………., 69, 70, 71, 72, ……….., 79, 80, 81, ………., 89, 90, 91, ………………......, 99
3-digit numbers:
100, 101, …….., 199, 200, 201, ……, 299, 300, ……., 399, 400, ………, 499,
500, ….., 599, 600, ……, 699, 700, …., 799, 800, 801, ……, 890, ……., 899,
900, 901, ………, 990, 991, ……………, 999.
4-digit numbers:
1000, 1001,……,1099,1100,1101,……,1199,1200,1201,…………,1299,
1300, ……, 1399, 1400, 1401, …….,1499, 1500, 1501,……., 1599, 1600,
1601, ….., 1699, 1700, 1701, ……, 1799, 1800, 1801,………, 1899, 1900,
1901, ......., 1999, 2000, 2001, ……., 2999, 3000, 3001, …….., 3999, 4000,
4001, ……, 4999, 5000, ……., 5999, 6000, ……, 6999, 7000, 7001, ………,
7999, 8000, 8001, ………., 8999, 9000, 9001, ….....,9999.
5-digit numbers:
10000, 10001, ……………………………………………………........., 19999,
20000, 20001, ………………………………………………………….., 29999,
30000, 30001, ………………………………………………………….., 39999,
40000, 40001, .................., 49999, 50000, ………………………….., 59999,
60000, 60001, ……………, 69999, 70000, ……………………… ....., 79999,
80000, 80001, ……………., 89999, 90000, ………………………........ 99999
Now 6-digit numbers begin with 99999 + 1 = 100000, i.e., hundred thousand.
1. Fill in the blanks:
(i) 1,00,000 more than 4,52,532 is ................
(ii) 10,000,000 more than 54,928,329 is ................
(iii) 10,00,000 less than 32,24,521 is ................
(iv) 100,000 less than 8,482,934 is ................
(v) 10,000 more than 99,999 is ................
(vi) 1,000 more than 56,784 is ................
(vii) 10,000 less than 39,948 is ................
Related Concept
● Numbers Showing on Spike Abacus.
● 1 Digit Number on Spike Abacus.
● 2 Digits Number on Spike Abacus.
● 3 Digits Number on Spike Abacus.
● 4 Digits Number on Spike Abacus.
● 5 Digits Number on Spike Abacus.
● Problems Related to Place Value.
● Example on Comparison of Numbers.
● Successor and Predecessor of a Whole Number.
● Formation of Numbers with the Given Digits.
● Formation of Greatest and Smallest Numbers.
● Examples on the Formation of Greatest and the Smallest Number.
You might like these
Worksheet on Divide by 10, 100 and 1000 Divisors |Quotient & Remainder
Practice the questions given in the worksheet on divide by 10, 100 and 1000 divisors to find the quotient and remainder if any. Find the quotient and remainder (if any): I. Divide the given numbers by 10 and find the Quotient and Remainder. II. Divide the given numbers by
Method of L.C.M. | Finding L.C.M. | Smallest Common Multiple | Common
We will discuss here about the method of l.c.m. (least common multiple). Let us consider the numbers 8, 12 and 16. Multiples of 8 are → 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, ......
Adding 4-digit Numbers with Regrouping | 4-digit Addition |Addition
We will learn adding 4-digit numbers with regrouping. Addition of 4-digit numbers can be done in the same way as we do addition of smaller numbers. We first arrange the numbers one below the other in place value columns and then we start adding from the ones place
Worksheet on Word Problems on Division | Division Word Problems
In worksheet on word problems on division, all grade students can practice the questions on word problems involving division. This exercise sheet on word problems on division can be practiced by the students to get more ideas to solve division problems.
Methods of Prime Factorization | Division Method | Factor Tree Method
In prime factorization, we factorise the numbers into prime numbers, called prime factors. There are two methods of prime factorization: 1. Division Method 2. Factor Tree Method
Adding 4-digit Numbers without Regrouping | 4-digit Addition |Addition
We will learn adding 4-digit numbers without regrouping. We first arrange the numbers one below the other in place value columns and then add the digits under each column as shown in the following examples. For example: 1. Add 1547 and 5231. Solution: Add the ones. 7 + 1 = 8
Worksheet on Adding 4-Digit Numbers with Regrouping |
In worksheet on adding 4-digit numbers with regrouping we will solve the addition of 4-digit numbers with regrouping or with carrying, 4-digit vertical addition, arrange in columns and add and missing numbers in 4-digit addition.
Formation of Greatest and Smallest Numbers | Arranging the Numbers
the greatest number is formed by arranging the given digits in descending order and the smallest number by arranging them in ascending order. The position of the digit at the extreme left of a number increases its place value. So the greatest digit should be placed at the
Word Problems on Multiplication |Multiplication Word Problem Worksheet
Word problems on multiplication for fourth grade students are solved here step by step. Problem Sums Involving Multiplication: 1. 24 folders each has 56 sheets of paper inside them. How many sheets of paper are there altogether? Solution: We can add 56 sheets 24 times
Find the Missing Digits | Missing Digits in Addition and Subtraction
How to find the missing digits in the blank spaces? Add the ONES: 5 + 9 = 14 Regroup as 1 Ten and 4 Ones Add the TENS: 2 + 1 carry over = 3 Write 2 in the box to make 3 + 2 = 5 Add the HUNDREDS: 4
Rounding off Numbers | Nearest Multiple of 10 | Nearest Whole Number
Rounding off numbers are discussed here, where we need to round a number. (i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left. (ii) If we purchase another thing and its cost is $15.78. The cost is rounded up
Worksheet on Word Problems on Addition|Word Problems Based on Addition
In 4th grade worksheet on word problems on addition, all grade students can practice the questions on word problems based on addition. This exercise sheet on addition can be practiced by the students to get more ideas to solve the worksheet on word problems on addition.
Worksheet on Methods of Prime Factorization |Prime Factors by Division
Practice the questions given in the worksheet on methods of prime factorization. 1. Each of the following is the prime factorization of a certain number. Find the number. (i) 2 × 5 × 7
Examples on the Formation of Greatest and the Smallest Number |Example
In examples on the formation of greatest and the smallest number we know that the procedure of arranging the numbers in ascending and descending order.
Even and Odd Numbers Between 1 and 100 | Even and Odd Numbers|Examples
All the even and odd numbers between 1 and 100 are discussed here. What are the even numbers from 1 to 100? The even numbers from 1 to 100 are:
From Formation of Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
What are Parallel Lines in Geometry? | Two Parallel Lines | Examples
Apr 19, 24 04:39 PM
In parallel lines when two lines do not intersect each other at any point even if they are extended to infinity. What are parallel lines in geometry? Two lines which do not intersect each other -
Perpendicular Lines | What are Perpendicular Lines in Geometry?|Symbol
Apr 19, 24 04:01 PM
In perpendicular lines when two intersecting lines a and b are said to be perpendicular to each other if one of the angles formed by them is a right angle. In other words, Set Square Set Square If two… -
Fundamental Geometrical Concepts | Point | Line | Properties of Lines
Apr 19, 24 01:50 PM
The fundamental geometrical concepts depend on three basic concepts — point, line and plane. The terms cannot be precisely defined. However, the meanings of these terms are explained through examples. -
What is a Polygon? | Simple Closed Curve | Triangle | Quadrilateral
Apr 19, 24 01:22 PM
What is a polygon? A simple closed curve made of three or more line-segments is called a polygon. A polygon has at least three line-segments. -
Simple Closed Curves | Types of Closed Curves | Collection of Curves
Apr 18, 24 01:36 AM
In simple closed curves the shapes are closed by line-segments or by a curved line. Triangle, quadrilateral, circle, etc., are examples of closed curves.