Division by 10 and 100 and 1000
Division by 10 and 100 and 1000 are explained here step by step. We know the following facts regarding division process:
1. (i) When any number is divided by 1, the quotient is the number itself.
(a) 7 ÷ 1 = 7
(b) 53 ÷ 1 = 53
(c) 275 ÷ 1 = 275
(ii) When a number (except 0) is divided by itself, the quotient is 1.
(a) 7 ÷7 = 1
(b) 53 ÷ 53 = 1
(c) 275 ÷ 275 = 1
(iii) When zero (0) is divided by any number, the quotient is zero (0), but no number can be divided by zero (0).
(a) 0 ÷ 8 = 0, 0/8 = 0, 0 ÷ 115 = 0, 0/115 = 0
(b) 0 ÷ 0 has no meaning, 10 ÷ 0 has no meaning, 15 ÷ 0 has no meaning.
2. Division by 10:
(i) 20 ÷ 10 = 2
(ii) 40 ÷10 = 4
(iii) 120 ÷ 10 = 12
(iv) 176 ÷ 10 = 17, remainder 6
When a number is divided by 10, the digits, except the digit at the
one's place, make the quotient and the digit at one's place becomes the
remainder.
As for example:
(i) 48 ÷ 10
Quotient = 4 Remainder = 8
(ii) 76 ÷ 10
Quotient = 7 Remainder = 6
(iii) 492 ÷ 10
Quotient = 49 Remainder = 2
(iv) 178 ÷ 10
Quotient = 17 Remainder = 8
(v) 569 ÷ 10
Quotient = 56 Remainder = 9
(vi) 4183 ÷ 10
Quotient = 418 Remainder = 3
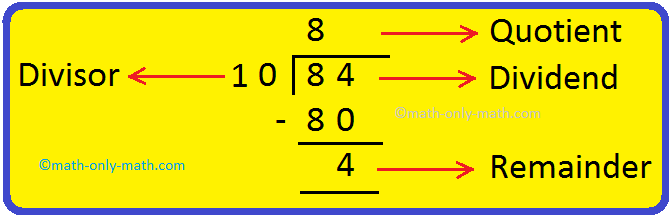
(vii) Divide 84 by 10.
Solution:
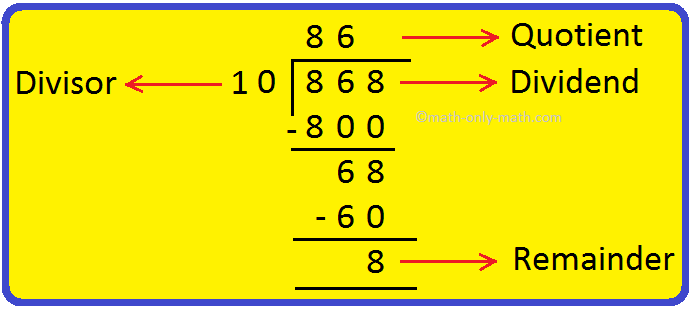
(vii) Divide 868 by 10.
Solution:
Thus, when a number is divided by 10, the remainder is always the digit of the unit place and the quotient is the number made by the remaining digits.
In other words, when we divide a number by 10, the digit at ones place of the given number becomes the remainder and the digits at the remaining places of the number given the quotient.
Therefore, notice that on dividing by 10, the digit in the ONES place forms the remainder, while the remaining digits form the quotient.
3. Division by 100:
(i) 500 ÷ 100 = 5
(ii) 700 ÷100 = 7
(iii) 752 ÷ 100 = 7, remainder 52
When a number is divided by 100, the quotient is the number made by the digits, except the digits at one's and ten's places. The number formed by ten's and one's digit of the dividend number is the remainder.
As for example:
(i) 476 ÷ 100
Will give quotient 4 remainder 76
(ii) 3479 ÷ 100
Will give quotient 34 remainder 79
The number of digits in the remainder is equal to the number of zeros in the divisor.
(iii) 527 ÷ 100
Quotient = 5 Remainder = 27
(iv) 609 ÷ 100
Quotient = 6 Remainder = 9
(v) 7635 ÷ 100
Quotient = 76 Remainder = 35
(vi) 7635 ÷ 100
Quotient = 30 Remainder = 79
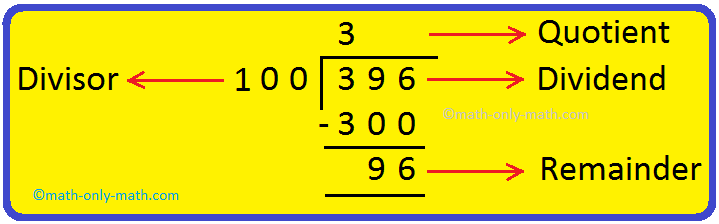
(vii) Divide 396 by 100.
Thus, when the dividend number is divided by 100, the extreme right two digits form the remainder and the rest of the digits form the quotient.
In other words, when we divide a number by 100, the digit at ones and tens place together of the given number forms the remainder and the digits at the remaining places of the number given the quotient.
Therefore, when we divide by 100, the two digits in the ONES and the TENS place form the remainder while the remaining digits form the quotient.
4. Division by 1000:
(i) 6000 ÷ 1000 = 6
(ii) 9000 ÷1000 = 9
(iii) 8542 ÷ 1000 = 8, remainder 542
(iv) 7294 ÷ 1000 = 7, remainder 294
Following this method, when we divide by 1000, the remainder will have 3 digits.
When
a number is divided by 1000, the quotient is the number made of the
digits except the digits at one's, ten's and hundred's place. The number
formed by these three digits is the remainder.
As for example:
(i) 1379 ÷ 1000
Will give quotient 1 remainder 379
(ii)45362 ÷ 1000
Will give quotient 45 remainder 362
The 3 digits in the ONES, TENS, HUNDREDS places form the remainder.
(iii) 3851 ÷ 1000
Quotient = 3 Remainder = 851
(iv) 9874 ÷ 1000
Quotient = 9 Remainder = 874
(v) 35786 ÷ 1000
Quotient = 35 Remainder = 786
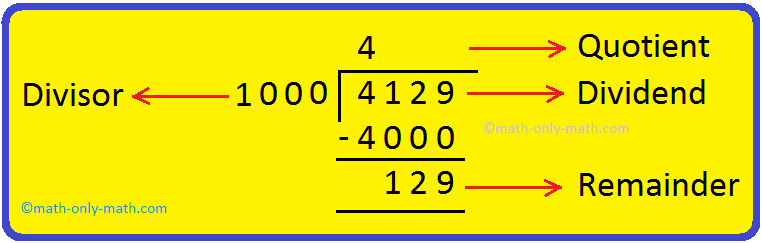
(vi) Divide 4129 by 1000.
Solution:
Thus, when the dividend number is divided by 1000, the extreme right three digits form the remainder and the rest digit/digits form the quotient.
In other words, when we divide a number by 1000, the digit at ones, tens and hundreds place together of the given number forms the remainder and the digits at the remaining places of the number given the quotient.
Note:
The zeros in the divisor help in getting the answer.
|
4532 ÷ 10 |
Q : 453 |
R : 2 |
|
4532 ÷ 100 |
Q : 45 |
R : 32 |
|
4532 ÷ 1000 |
Q : 4 |
R : 532 |
Division of a number by 20, 30, 40.....
(i) 80 ÷ 20
20 × ____ = 80
2 × 4 = 8
So, 20 × 4 = 80
(ii) 140 ÷ 70
70 × ____ = 140
7 × 2 = 14
So, 70 × 2 = 140
(iii) 900 ÷30
30 × ____ = 900
3 × 3 = 9
30 × 3 = 90
So, 30 × 30 = 900
(iv) 320 ÷ 80
80 × ____ = 320
8 × 4 = 32
So, 80 × 4 = 320
Remember:
I: When we divide a number by 10, the quotient is obtained by removing the first digit from the right, i.e. digit in the ones place. The digit in the units place is the remainder.
II: When we divide a number by 100, the quotient is obtained by removing the first two digits from the right, i.e. digit in the tens and ones places. The number formed by the digits in tens and ones places is the remainder.
III: When we divide a number by 1000, the quotient is obtained by removing the first three digits from the right, i.e. digit in the hundreds, tens and ones places. The number formed by the digits in hundreds, tens and ones places is the remainder.
Questions and Answers on Division by 10, 100 and 1000:
1. (i) 400 ÷ 10 = Q = ............ R = ............
(ii) 352 ÷ 100 = Q = ............ R = ............
(iii) 384 ÷ 100 = Q = ............ R = ............
(iv) 45 ÷ 10 = Q = ............ R = ............
(v) 295 ÷ 10 = Q = ............ R = ............
(vi) 4072 ÷ 100 = Q = ............ R = ............
(vii) 37 ÷ 10 = Q = ............ R = ............
(viii) 9675 ÷ 1000 = Q = ............ R = ............
(ix) 6814 ÷ 1000 = Q = ............ R = ............
(x) 3596 ÷ 100 = Q = ............ R = ............
Answer:
1. (i) Q = 40; R = 0
(ii) Q = 3; R = 52
(iii) Q = 3; R = 84
(iv) Q = 4; R = 5
(v) Q = 29; R = 5
(vi) Q = 40; R = 72
(vii) Q = 3; R = 7
(viii) Q = 9; R = 675
(ix) Q = 6; R = 814
(x) Q = 35; R = 96
Related Concept
● Addition
● Check for Subtraction and Addition
● Word Problems Involving Addition and Subtraction
● Estimating Sums and Differences
● Multiply a Number by a 2-Digit Number
● Multiplication of a Number by a 3-Digit Number
● Word Problems on Multiplication
● Division of Two-Digit by a One-Digit Numbers
● Division of Four-Digit by a One-Digit Numbers
● Division by 10 and 100 and 1000
● Division by Two-Digit Numbers
4th Grade Math Activities
From Division by 10 and 100 and 1000 to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Addition of Capacity | Add the Different Units of Capacity | Examples
Nov 14, 24 03:03 PM
In addition of capacity we will learn how to add the different units of capacity and volume together. While adding we need to follow that the units of capacity i.e., liter and milliliter -
Measuring Capacity | Standard Unit of Capacity | Litre | Millilitres
Nov 14, 24 02:40 PM
We will discuss about measuring capacity. The milkman measures milk in liters. Petrol is given in liters. Mobil oil is sold in liters. Two milk bottles contain 1 liter of milk. One milk bottle -
Subtraction of Mass | Difference Between the Units of Mass | Examples
Nov 14, 24 09:16 AM
In subtraction of mass we will learn how to find the difference between the units of mass or weight. While subtracting we need to follow that the units of mass i.e., kilogram and gram -
Worksheet on Subtraction of Mass |Word Problems on Subtraction of Mass
Nov 13, 24 02:00 PM
Practice the third grade math worksheet on subtraction of mass or weight. This sheet provides different types of questions where you need to arrange the values of mass under different columns -
Worksheet on Addition of Mass | Word problems on Addition of Mass
Nov 13, 24 10:24 AM
Practice the third grade math worksheet on addition of mass/weight. This sheet provides different types of questions where you need to arrange the values of mass under different columns
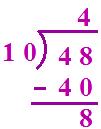
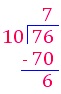
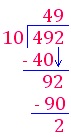
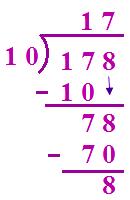
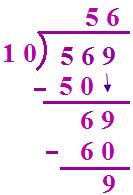
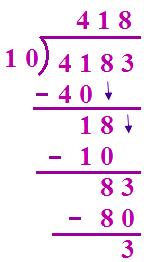
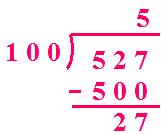
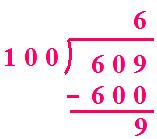
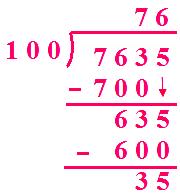
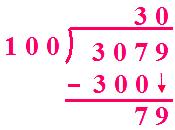
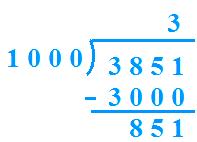
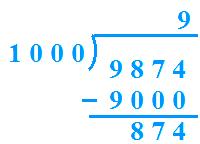
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.