Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Multiplication
In multiplication we know how to multiply a one, two or three-digit number by another 1 or 2-digit number. We also know how to multiply a four-digit number by a 2-digit number. We also know the different methods of multiplication. Here, we shall make use of the methods and procedures learnt previously in multiplying larger numbers.
The numbers that are being multiplied are called factors.
The answer of a multiplication operation is called a product.
Let us recall the properties of multiplication:
I. The product does not change when the order of the numbers is changed.
5 × 4 = 4 × 5
6 × 3 = 3 × 6
II. The product does not change when the grouping of numbers is changed.
(6 × 7) × 4 = 6 × (7 × 4)
2 × (5 × 3) = (2 × 5) × 3
III. The product of a number and 1 is the number itself.
96 × 1 = 96
72 × 1 = 72
IV. The product of a number and 0 is 0.
754 × 0 = 0
316 × 0 = 0
For examples:
40 × 5 = 200
400 × 5 = 2000
4000 × 5 = 20000
Now, we will recall how to do multiplication of a number by a 1-digit number.
Examples on Expanded Notation Method:
1. Use expanded notation to multiply 64 and 8.
Answer: 512
3 and 4 digit numbers can also be multiplied by a 1 digit number using the expanded notation method.
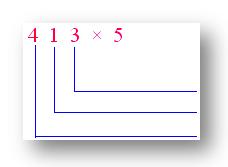
2. Use expanded notation to multiply 413 by 5.
Answer: 2065
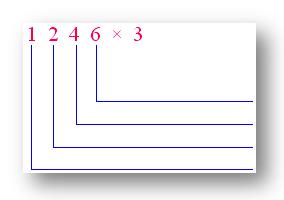
3. Use expanded notation to multiply 1246 by 3.
Answer: 3738
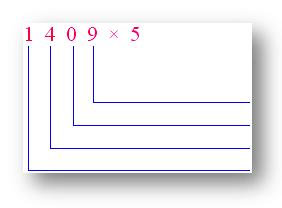
4. Use expanded notation to find the product of 1409 and 5.
Answer: 7045
Let us first revise the process of multiplication.
Consider the following:
1. Multiply 215 by 7
Solution:
(i) (Expanded notation method)
215 × 7 = (200 + 10 + 5) × 7 1 4 0 0
= 200 × 7 + 10 × 7 + 5 × 7 + 7 0
= 1400 + 70 + 35 + 3 5
= 1505 1 5 0 5
(ii) (Column method)
|
Product = 1505 |
(i) 5 ones × 7 = 35 = 3 tens + 5 ones |
2. Multiply 6103 by 8
Solution:
(i) (Expanded notation method)
6103 × 8 = (6000 + 100 + 0 + 3) × 8 4 8 0 0 0
= 48000 + 800 + 0 + 24 + 8 0 0
= 48824 + 0
+ 2 4
4 8 8 2 4
(ii) (Column method)
|
Product = 4 8 8 2 4 |
(i) 3 one × 8 = 24 ones = 2 tens + 4 ones |
So, 6103 × 8 = 48824
3. Find the product of 2113 and 3 using column method.
Solution:
You might like these
Terms Used in Division | Dividend | Divisor | Quotient | Remainder
The terms used in division are dividend, divisor, quotient and remainder. Division is repeated subtraction. For example: 24 ÷ 6 How many times would you subtract 6 from 24 to reach 0?
Successor and Predecessor | Successor of a Whole Number | Predecessor
The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number. For example, 9,99,99,999 is predecessor of 10,00,00,000 or we can also
Worksheets on Comparison of Numbers | Find the Greatest Number
In worksheets on comparison of numbers students can practice the questions for fourth grade to compare numbers. This worksheet contains questions on numbers like to find the greatest number, arranging the numbers etc…. Find the greatest number:
Number Worksheets | Practice Different Questions on Numbers | Answers
In number worksheets, students can practice different questions on numbers from printable free worksheets for grade 4 math on numbers. Write the number which is 1 more than 9? Write the number which
Comparison of Numbers | Compare Numbers Rules | Examples of Comparison
Rule I: We know that a number with more digits is always greater than the number with less number of digits. Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits. To learn
Formation of Numbers | Smallest and Greatest Number| Number Formation
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,
Formation of Numbers with the Given Digits |Making Numbers with Digits
In formation of numbers with the given digits we may say that a number is an arranged group of digits. Numbers may be formed with or without the repetition of digits.
Formation of Greatest and Smallest Numbers | Arranging the Numbers
the greatest number is formed by arranging the given digits in descending order and the smallest number by arranging them in ascending order. The position of the digit at the extreme left of a number increases its place value. So the greatest digit should be placed at the
Place Value and Face Value | Place and Face Value of Larger Number
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know that the position of a digit in a number determines its corresponding value
Expanded Form of a Number | Writing Numbers in Expanded Form | Values
We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its digits. This is shown here: In 2385, the place values of the digits are
Related Concept
● Addition
● Check for Subtraction and Addition
● Word Problems Involving Addition and Subtraction
● Estimating Sums and Differences
● Multiply a Number by a 2-Digit Number
● Multiplication of a Number by a 3-Digit Number
● Word Problems on Multiplication
● Division of Two-Digit by a One-Digit Numbers
● Division of Four-Digit by a One-Digit Numbers
● Division by 10 and 100 and 1000
● Division by Two-Digit Numbers
4th Grade Math Activities
From Multiplication to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
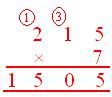
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.