Word Problems Involving
Addition and Subtraction
Word problems involving addition and subtraction are discussed here step by step.
There are no magic rules to make problem solving easy, but a systematic approach can help to the problems easily.
Word problems based on addition are broadly of two types:
(a) When objects of two or more collections are put together.
For example:
Amy has 20 lemon sweets and 14 orange sweets. What is the total number of sweets Amy has?
(b) When an increase in number takes place.
For example:
Victor has 14 stamps. His friend gave him 23 stamps. How many stamps does Victor have in all?
The key words used in problems involving addition are:
sum; total; in all; all together.
Word problems based on subtraction are of several types:
(a) Partitioning : Take away, remove, given away.
(b) Reducing : Find out how much has been given away or how much remains.
(c) Comparison : More than / less than.
(d) Inverse of addition : How much more to be added.
The key words to look out for in a problem sum involving subtraction are:
take away; how many more ; how many less ; how many left ; greater ; smaller.
1. The girls had 3 weeks to sell tickets for their play. In the first
week, they sold 75 tickets. In the second week they sold 108 tickets and
in the third week they sold 210 tickets. How may tickets did they sell
in all?
Tickets sold in the first week = 75
Tickets sold in the second week = 108
Tickets sold in the third week = 210
Total number of tickets sold = 75 + 108 + 210 = 393
Answer: 393 tickets were sold in all.
2. Mr. Bose spent $450 for petrol on Wednesday. He spent $125 more than
that on Thursday. How much did he spend on petrol on those two days.
This problem has to be solved in two steps.
Step 1: Money spent for petrol on Thursday
450 + 125 = $575
Step 2: Money spent for petrol on both days
450 + 575 = $1025
Examples on word problems on addition and subtraction:
1. What is the sum of 4373, 4191 and 3127?
Solution:
The numbers are arranged in columns and added.
|
(i) Ones are added: 3 + 1 + 7 = 11 = 1 Ten + 1 one (ii) Tens are added: 1 + 7 + 9 + 2 = 19 tens = 1 hundred + 9 ten (iii) Hundreds are added: 1 + 3 + 1 + 1 = 6 Hundred (iv) Thousands are added: 4 + 4 + 3 = 11 Thousand |
Therefore, sum =11,691
2. What is the difference of 3867 and 1298?
Solution:
The numbers are arranged in columns and subtracted:
|
(i) Ones are subtracted: 7 < 8 1 is borrowed from 6 ten. So, 1 T or 10 + 7 = 17, 17 - 8 = 9 (ii) Tens are subtracted; 5 T < 9 T, So, 1 H or 10 T is borrowed from 8 H, 1 H = 10 T + 5 T = 15T 15T - 9T = 6 (iii) Hundreds are subtracted 7 H – 2 H = 5 H (iv) Thousands are subtracted 3 Th – 1 Th = 2 Th |
Therefore, difference = 2569
3. Subtract 4358 from the sum of 5632 and 1324.
Solution:
Sum of 5632 and 1324
Difference of 6956 and 4358
|
(i) 6 < 8, 1 T or 10 ones are borrowed 1 T or 10+ 6 =16, 16 - 8 = 8 (ii) 4 T < 5 T, 1 H or 10 T is borrowed 10 T + 4 T = 14 T, 14 T – 5 T = 9 T (iii) 8 H – 3 H = 5 H (iv) 6 Th – 4 Th = 2 Th |
Therefore, 2598 is the answer.
4. Find the number, which is
(i) 1240 greater than 3267.
(ii) 1353 smaller than 5292.
Solution:
(i) The number is 1240 more than 3267
Therefore, the number = 3267 + 1240 or = 4507
(ii) The number is 1353 less than 5292
= 5292 – 1353 or
= 3939
5. The population of a town is 16732. If there are 9569 males then find the number of females in the town.
Solution:
|
Population of the town Number of males Therefore, number of females |
= 1 6 7 3 2 = - 9 5 6 9 = 7 1 6 3 |
6. In a factory there are 35,675 workers. 10,750 workers come in
the first shift, 12,650 workers in the second shift and the rest come in
the third shift. How many workers come in the third shift?
Solution:
Number of workers coming in the first and second shift
= 10750 + 12650 = 23400
Therefore, number of workers coming in the third shift = 35675 - 23400 = 12275
Related Concept
● Addition
● Check for Subtraction and Addition
● Word Problems Involving Addition and Subtraction
● Estimating Sums and Differences
● Multiply a Number by a 2-Digit Number
● Multiplication of a Number by a 3-Digit Number
● Word Problems on Multiplication
● Division of Two-Digit by a One-Digit Numbers
● Division of Four-Digit by a One-Digit Numbers
● Division by 10 and 100 and 1000
● Division by Two-Digit Numbers
4th Grade Math Activities
From Word Problems Involving Addition and Subtraction to
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 12, 24 09:20 AM
2nd grade geometry worksheet -
Types of Lines |Straight Lines|Curved Lines|Horizontal Lines| Vertical
Dec 09, 24 10:39 PM
What are the different types of lines? There are two different kinds of lines. (i) Straight line and (ii) Curved line. There are three different types of straight lines. (i) Horizontal lines, (ii) Ver… -
Points and Line Segment | Two Points in a Curved Surface | Curve Line
Dec 09, 24 01:08 AM
We will discuss here about points and line segment. We know when two lines meet we get a point. When two points on a plane surface are joined, a straight line segment is obtained. -
Solid Shapes | Basic Geometric Shapes | Common Solid Figures | Plane
Dec 08, 24 11:19 PM
We will discuss about basic solid shapes. We see a variety of solid objects in our surroundings. Solid objects have one or more shapes like the following. Match the objects with similar shape. -
2nd grade math Worksheets | Free Math Worksheets | By Grade and Topic
Dec 07, 24 03:38 PM
2nd grade math worksheets is carefully planned and thoughtfully presented on mathematics for the students.
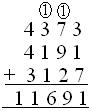
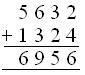
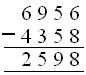
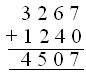
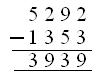
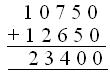
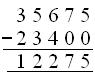
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.