Volume of a Cuboid

Cuboid is a solid box whose every surface is a rectangle of same area or different areas.

A cuboid will have a length, breadth and height.

Hence we can conclude that volume is 3 dimensional. To measure the volumes we need to know the measure 3 sides.

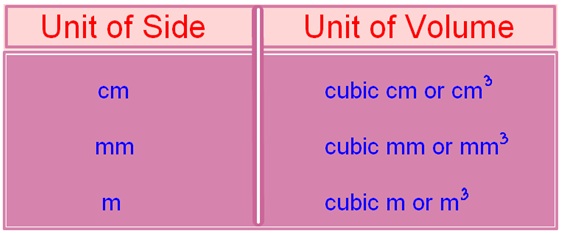
Since volume involves 3 sides it is measured in cubic units.

Volume of a cuboid = (length × breadth × height) cubic units.

= (l × b × h) cubic units.

   (Since area = ℓ × b)

Volume of a cuboid = area of one surface × height cubic units

1. Let us look at the given cuboid.

The length of the cuboid = 5 cm

The breadth of the cuboid = 3 cm

The height of cuboid (thickness) = 2 cm

The number of 1 cm cubes in the given cuboid = 30 cubes = 5 × 3 × 2

We find that volume of the given cuboid with length 5 cm, breadth 3 cm and height 2 cm is 30 cu cm.

Therefore, volume of a cuboid = length × breadth × height

A cuboid is a solid figure which has length, breadth and height. It is a rectangular solid.

2. In the figure, we see a rectangular solid whose length is 5 cm, breadth is 3 cm and height is 3 cm.

For finding its volume, we divide it into unit cubes of 1 cm side.

We find that topmost layer contains 5 × 3 = 15 cubes.

Total number of such layers is 3.

So, the total cubes are 15 × 3 = 45

So, the volume of this cuboid is 45 cm³ because the volume of each cube is 1 cubic cm or 1 cm³

Volume of a cuboid = length × breadth × height

                         v = ℓ × b × h

For example, in the above case,

ℓ = 5 cm

b = 3 cm and

h = 3 cm

Therefore, volume of the given cuboid = (5 × 3 × 3) cm³ = 45 cm³

Word Problems on Volume of a Cuboid

Solved examples on volume of a cuboid:

1. Find the volume of a cuboid of dimensions 14 cm × 12 cm × 8 cm.

Solution:

Volume of cuboid = length × breadth × height.

Here, length = 14 cm, breadth = 12 cm and height = 8 cm.

Volume of cuboid = 14 × 12 × 8 cubic cm.

= 1344 cubic cm.

Therefore, volume of cuboid = 1344 cubic cm.

2. Michael made a shoe box with length 8 cm, breadth 6 cm and height 6 cm. Find the volume of the box.

Solution:

Volume of the shoe box = Length × breadth × height.

                                   = 8 × 6 × 6

                                   = 288 cu cm.

3. A fish tank is 40 cm long, 15 cm broad and 10 cm high. What is its volume in cu cm?

Solution:

The length of the fish tank = 40 cm

The breadth of the fish tank = 15 cm

The height of the fish tank = 10 cm

Therefore, the volume of the fish tank = length × breadth × height.

                                                        = 40 × 15 × 10 cu. cm

                                                        = 6000 cu cm.

4. Find the volume of a cuboid of dimensions 14 cm × 50 mm × 10 cm.

Solution:

Here, length = 14 cm,

[Given, breadth = 50 mm; we need to convert breadth to same unit and then solve. We know, 10 mm = 1 cm. Therefore, 50 mm = 50/10 cm = 5 cm].

Breadth = 5 cm,

Height = 10 cm.

Volume of cuboid = length × breadth × height.

                          = 14 × 5 × 10

                          = 700 cubic cm.

Therefore, volume of cuboid = 700 cubic cm.

Note: In a cuboid, when the length, breadth and height are of different units, convert them to a same unit and then solve.

5. Find the volume of a cuboid of dimensions 17 mm × 0.2 cm × 12 mm in cu. cm.

Solution:

Given, length = 17 mm.

We know, 10 mm = 1 cm.

= 17/10 cm.

= 1.7 cm.

Therefore, length = 1.7 cm.

Similarly, height = 12 mm.

We know, 10 mm = 1 cm.

= 12/10 cm.

= 1.2 cm.

Therefore, height = 1.2 cm.

Volume of cuboid = length × breadth × height.

Length = 1.7 cm, breadth = 0.2 cm and height = 1.2 cm.

           = 1.7 × 0.2 × 1.2 cu. cm.

           = 0.408 cu. cm.

Therefore, volume of cuboid = 0.408 cubic cm.

6. Find the number of cubical boxes of cubical side 3 cm which can be accommodated in carton of dimensions 15 cm × 9 cm × 12 cm.

Solution:

Volume of box = side × side × side.

                      = 3 × 3 × 3

                      = 27 cu. cm.

Volume of carton = length × breadth × height.

                          = 15 × 9 × 12

                          = 1620 cu. cm.

Number of boxes = Volume of carton/Volume of each box.

                          = 1620/27

                          = 60

Therefore, number of cubical boxes = 60.

7. How many bricks each 25 cm long, 10 cm wide and 7.5 cm thick will be required for a wall 20 m long, 2 m high and 0.75 m thick? If bricks sell at $900 per thousand what will it cost to build the wall?

Solution:

Volume of the wall = 20 m × 2 m × 0.75 m

                           = 20 × 100 cm × 2 × 100 cm × 0.75 × 100 cm

Volume of brick = 25 cm × 10 cm × 7.5 cm

Number of bricks = $\frac{\textrm{Volume of the wall}}{\textrm{Volume of the brick}}$

                         = $\frac{20 × 100 × 2 × 100 × 0.75 × 100}{25 × 10 × 7.5}$

                         = 16000

The number of bricks = 16000

The cost of 1 thousand bricks = $ 900

The cost of building the wall = $ 900 × 16 = $ 14400

Note: While calculating the volume of a cuboid all the dimensions should be changed into the same unit. 

8. Find the volume of a cuboidal tank whose length, breadth and height are 10 m, 8 m, and 5 m respectively.

Solution:

Length of cuboidal tank = 10 m

Breadth of cuboidal tank = 5 m

Height of cuboidal tank = 8 m

Volume of cuboidal tank = length × breadth × height 

                                   = 10 m × 8 m × 5 m

                                   = 400 m³

Worksheet on Volume of a Cuboid

Questions and Answers on Cuboid:

1. Find the volume of each of the cuboids.

(i) Length = 5 cm, Breadth = 4 cm and Height = 3 cm

(ii) Length = 15 m, Breadth = 10 m and Height = 2 m

(iii) Length = 0.5 m, Breadth = 3 m and Height = 4 m

(iv) Length = 3.2 cm, Breadth = 2 cm and Height = 8 cm

(v) Length = 5 m, Breadth = 1.5 m and Height = 1.2 m

Answers:

1. (i) 60 cu. cm

(ii) 300 cu. m

(iii) 6 cu. m

(iv) 51.2 cu. cm

(v) 9 cu. m

2. Find the volume of these tanks.

(i) Length = 16 cm, Breadth = 60 cm and Height = 20 cm

(ii) Length = 6 m, Breadth = 3 m and Height = 5 m

(iii) Length = 2 m, Breadth = 1.5 m and Height = 1.5 m

(iv) Length = 80 cm, Breadth = 20 cm and Height = 40 cm

(v) Length = 1.2 m, Breadth = 1.2 m and Height = 1 m

Answers:

2. (i) 19200 cu. cm

(ii) 90 cu. m

(iii) 4.5 cu. m

(iv) 64,000 cu. cm

(v) 1.44 cu. m

3. Find the volume of cuboids having the following measures.

Answers:

3. (i) 153 cm³

(ii) 1368 cm³

(iii) 15250 cm³

(iv) 1488 m³

(v) 112 m³

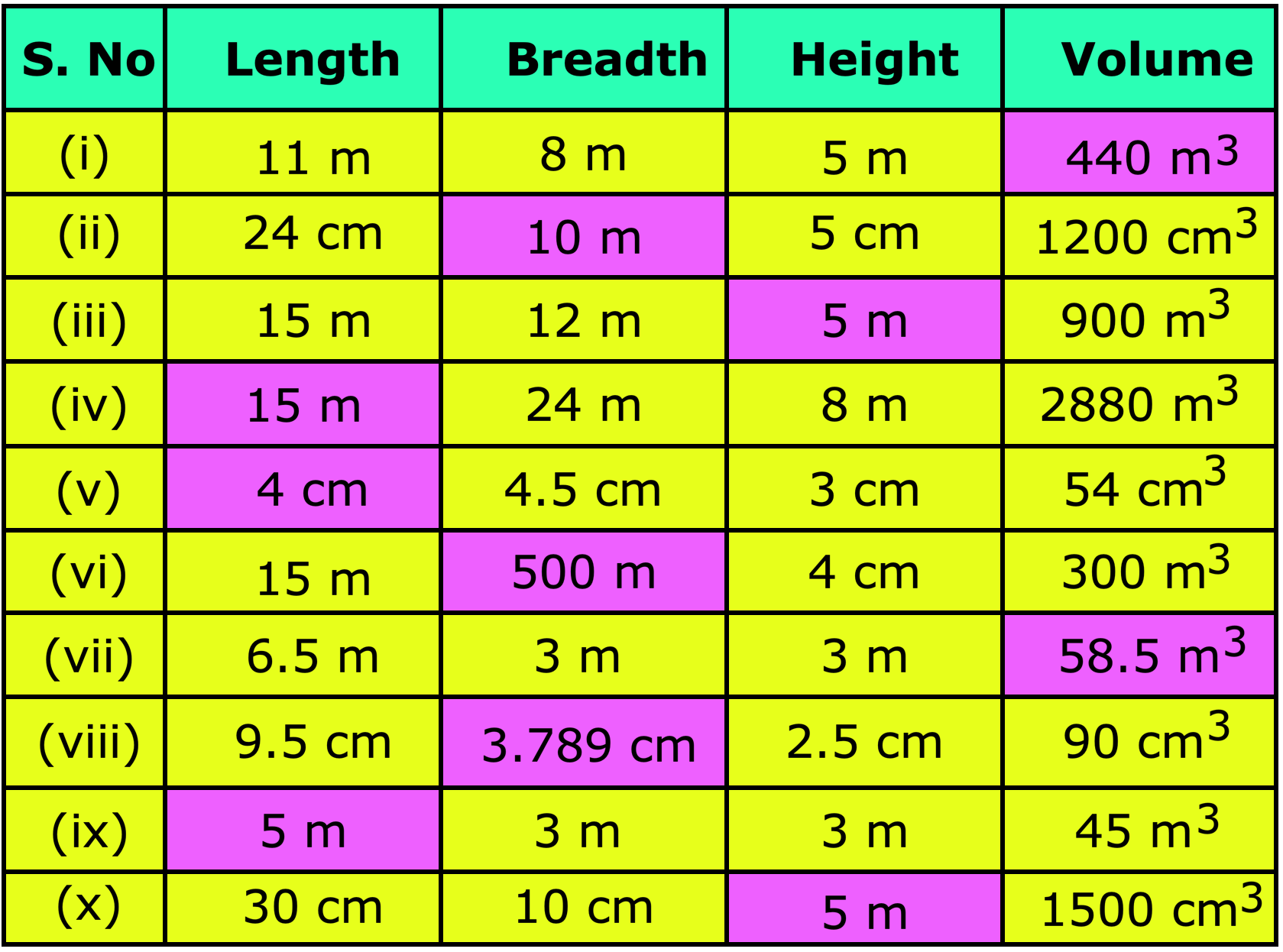
4. Dimensions of the different cuboids are given below. Fill in the missing measures in the given table:

Answer:

4. 

● Volume.

Units of Volume

Cube.

Cuboid.

Practice Test on Volume.

Worksheet on Volume.

5th Grade Geometry

5th Grade Math Problems

From Volume of a Cuboid to HOME PAGE