Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Math Problem Answers
Math problem answers are solved here step-by-step to keep the explanation clear to the students. In Math-Only-Math you'll find abundant selection of all types of math questions for all the grades with the complete step-by-step solutions.
Parents and teachers can follow math-only-math to help their students to improve and polish their knowledge. Children can practice the worksheets of all the grades and on all the topics to increase their knowledge.
Various types of Math Problem Answers are solved here.
1. Mrs. Rodger got a weekly raise of $145. If she gets paid every other week, write an integer describing how the raise will affect her paycheck.
Solution:
Let the 1st paycheck be x (integer).
Mrs. Rodger got a weekly raise of $ 145.
So after completing the 1st week she will get $ (x+145).
Similarly after completing the 2nd week she will get $ (x + 145) + $ 145.
= $ (x + 145 + 145)
= $ (x + 290)
So in this way end of every week her salary will increase by $ 145.
2. The value of x + x(xx) when x = 2 is:
(a) 10, (b) 16, (c) 18, (d) 36, (e) 64
Solution:
x + x(xx)
Put the value of x = 2 in the above expression we get,
2 + 2(22)
= 2 + 2(2 × 2)
= 2 + 2(4)
= 2 + 8
= 10
Answer: (a)
3. Mr. Jones sold two pipes at $1.20 each. Based on the cost, his
profit one was 20% and his loss on the other was 20%. On the sale of the
pipes, he:
(a) broke even, (b) lost 4 cents, (c) gained 4 cents, (d) lost 10 cents, (e) gained 10 cents
Solution:
Selling price of the first pipe = $1.20
Profit = 20%
Let’s try to find the cost price of the first pipe
CP = Selling price - Profit
CP = 1.20 - 20% of CP
CP = 1.20 - 0.20CP
CP + 0.20CP = 1.20
1.20CP = 1.20
CP = \(\frac{1.20}{1.20}\)
CP = $ 1
Selling price of the Second pipe = $1.20
Loss = 20%
Let’s try to find the cost price of the second pipe
CP = Selling price + Loss
CP = 1.20 + 20% of CP
CP = 1.20 + 0.20CP
CP - 0.20CP = 1.20
0.80CP = 1.20
CP = \(\frac{1.20}{0.80}\)
CP = $1.50
Therefore, total cost price of the two pipes = $1.00 + $1.50 = $2.50
And total selling price of the two pipes = $1.20 + $1.20 = $2.40
Loss = $2.50 – $2.40 = $0.10
Therefore, Mr. Jones loss 10 cents.
Answer: (d)
4. The distance light travels in one year is approximately 5,870,000,000,000 miles. The distance light travels in 100 years is:(a) 587 × 108 miles, (b) 587 × 1010 miles, (c) 587 × 10-10 miles, (d) 587 × 1012 miles, (e) 587 × 10-12 miles
Solution:
The distance of the light travels in 100 years is:
5,870,000,000,000 × 100 miles.
= 587,000,000,000,000 miles.
= 587 × 1012 miles.
Answer: (d)
5. A man has $ 10,000 to invest. He invests $ 4000 at 5 % and $ 3500
at 4 %. In order to have a yearly income of $ 500, he must invest the
remainder at:
(a) 6 % , (b) 6.1 %, (c) 6.2 %, (d) 6.3 %, (e) 6.4 %
Solution:
Income from $ 4000 at 5 % in one year = $ 4000 of 5 %.
= $ 4000 × 5/100.
= $ 4000 × 0.05.
= $ 200.
Income from $ 3500 at 4 % in one year = $ 3500 of 4 %.
= $ 3500 × 4/100.
= $ 3500 × 0.04.
= $ 140.
Total income from 4000 at 5 % and 3500 at 4 % = $ 200 + $ 140 = $ 340.
Remaining income amount in order to have a yearly income of $ 500
= $ 500 - $ 340.
= $ 160.
Total invested amount = $ 4000 + $ 3500 = $7500.
Remaining invest amount = $ 10000 - $ 7500 = $ 2500.
We know that, Interest = Principal × Rate × Time
Interest = $ 160,
Principal = $ 2500,
Rate = r [we need to find the value of r],
Time = 1 year.
160 = 2500 × r × 1.
160 = 2500r
160/2500 = 2500r/2500 [divide both sides by 2500]
0.064 = r
r = 0.064
Change it to a percent by moving the decimal to the right two places
r = 6.4 %
Therefore, he invested the remaining amount $ 2500 at 6.4 % in order to get $ 500 income every year.
Answer: (e)
6. Jones covered a distance of 50 miles on his first trip. On a later
trip he traveled 300 miles while going three times as fast. His new
time compared with the old time was:
(a) three times as much, (b) twice as much, (c) the same, (d) half as much, (e) a third as much
Solution:
Let speed of the 1st trip x miles / hr. and speed of the 2nd trip 3x / hr.
We know that
Speed = Distance/Time.
Or, Time = Distance/Speed.
So, times taken to covered a distance of 50 miles on his first trip = 50/x hr.
And times taken to covered a distance of 300 miles on his later trip = 300/3x hr.
= 100/x hr.
So we can clearly see that his new time compared with the old time was: twice as much.
Answer: (b)
(a) -10.0, (b) -0.5, (c) -0.4, (d) -0.2, (e) 10.0
Solution:
(0.2)x = 2.
Taking log on both sides
log (0.2)x = log 2.
x log (0.2) = 0.3010, [since log 2 = 0.3010].
x log (2/10) = 0.3010.
x [log 2 - log 10] = 0.3010.
x [log 2 - 1] = 0.3010,[since log 10=1].
x [0.3010 -1] = 0.3010, [since log 2 = 0.3010].
x[-0.699] = 0.3010.
x = 0.3010/-0.699.
x = -0.4306….
x = -0.4 (nearest tenth)
Answer: (c)
8. If 102y = 25, then 10-y equals:
(a) -1/5, (b) 1/625, (c) 1/50, (d) 1/25, (e) 1/5
Solution:
102y = 25
(10y)2 = 52
10y = 5
1/10y = 1/5
10-y = 1/5
Answer: (e)
9. The fraction (5x-11)/(2x2 + x - 6) was obtained by adding the two fractions A/(x + 2) and B/(2x - 3). The values of A and B must be, respectively:
(a) 5x, -11, (b) -11, 5x, (c) -1, 3, (d) 3, -1, (e) 5, -11
Solution:
Answer: (d)
10. The sum of three numbers is 98. The ratio of the first to the second is 2/3, and the ratio of the second to the third is 5/8. The second number is:
(a) 15, (b) 20, (c) 30, (d) 32, (e) 33
Solution:
Let the three numbers be x, y and z.
Sum of the numbers is 98.
x + y + z = 98………………(i)
The ratio of the first to the second is 2/3.
x/y = 2/3.
x = 2/3 × y.
x = 2y/3.
The ratio of the second to the third is 5/8.
y/z = 5/8.
z/y = 8/5.
z = 8/5 × y.
z = 8y/5.
Put the value of x = 2y/3 and z = 8y/5 in (i).
2y/3 + y + 8y/5 = 98
49y/15 = 98.
49y = 98 × 15.
49y = 1470.
y = 1470/49.
y = 30 .
Therefore, the second number is 30.
Answer: (c)
11. Kalin walks at a constant rate of 5/8 kilometers per hour. The beach is 3/4 kilometers from his home. How long does it take Kalin to walk from his home to the beach?
Solution:
Speed = \(\frac{5}{8}\) kilometers per hour.
Distance = \(\frac{3}{4}\) kilometers
Distance = Speed × Time
or, Time = Distance/Speed
= (\(\frac{3}{4}\) ÷ \(\frac{5}{8}\)) hours
= (\(\frac{3}{4}\) × \(\frac{8}{5}\)) hours
= \(\frac{24}{20}\) hours
= \(\frac{6}{5}\) hours
= 1\(\frac{1}{5}\) hours
Answer: 1\(\frac{1}{5}\) hours
12. The cost price of one refrigerator is $23,547. How many refrigerators can be purchased for $588,675?
Solution:
Total amount = $588,675
Cost price of one refrigerator = $23,547.
No. of refrigerators = $588,675 ÷ $23,547 = 25
Answer: 25
13. In an University auditorium each row has 35 seats. Determine the minimum number of rows required to seat 1,575 students at a time.
Solution:
Total number of seats = 1,575
Each row has 35 seats.
No. of rows required = 1,575 ÷ 35 = 45
Answer: 45
14. What least number must be added to 15896 to get a number exactly divisible by 29?
Solution:
First divide 15896 by 29.
15896 = 29 × 548 + 4
The remainder is 4
Therefore, we need to add 4 to 15896 it will exactly divisible by 29.
Answer: 29
More Math Problem Answers
15. Find the largest 6-digit number exactly divisible by 174.
Solution:
The largest 6-digit number = 999999
Now divide the largest 6-digit number (999999) by 174
999999 = 174 × 5747 + 21
Remainder = 21
Now subtract the remainder 21 from the largest 6-digit number 999999.
Therefore, 999999 - 21 = 999978 is the largest 6-digit number exactly divisible by 174.
Answer: 999978
16. On diving 80,256 by 187, the remainder is 33. Find the quotient.
Solution:
Dividend = Divisor × Quotient + Remainder
80,256 = 187 × Quotient + 33
187 × Quotient = 80,256 - 33
187 × Quotient = 80223
Quotient = 80223 ÷ 187 = 429
Answer: 429
17. During prayer time in a school, 35 students stand in each row. Find the minimum number of rows if there are 1,575 students in that school.
Solution:
Number of students in each row = 35
Number of row = 1,575 ÷ 35 = 45
Answer: 45
Math Problem Answers
18. A motorcycle travels 1494 km in 18 hours. What is the average speed of the car?
Solution:
Distance traveled = 1494 km
Time = 18 hours
Average speed = Distance traveled ÷ Time
= (1494 ÷ 18) km/hr
= 83 km/hr
Answer: 83 km/hr
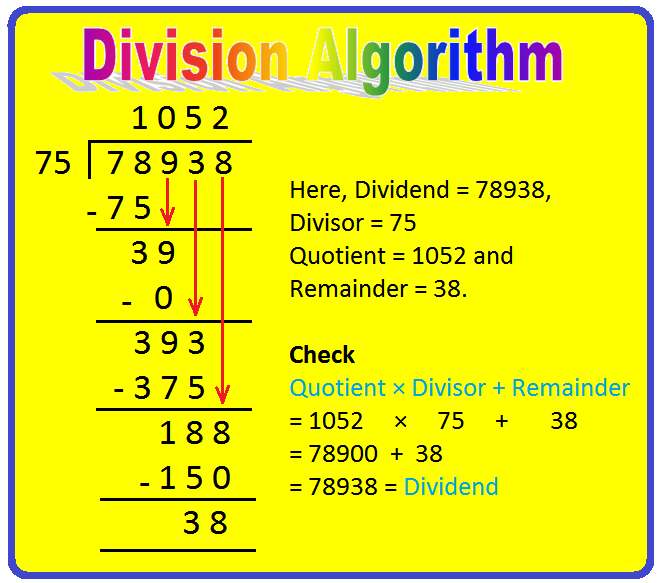
19. Divide 78938 by 75 and check the result by division algorithm.
Solution:
By actual division, we have
Here, dividend = 78938,
divisor 75
quotient 1052 and
remainder 38.
Check
Quotient × Divisor + Remainder
= 1052 × 75 + 38
= 78900 + 38
= 78938 = dividend
Math Problem Answers
20. Find the number which when divided by 67 gives 17 as quotient and 11 as remainder.
Solution:
Here, divisor = 67, quotient = 17 and remainder 11
By division algorithm, we have
Dividend = Divisor × Quotient + Remainder
= 67 × 17 + 11
= 1,139 + 11
= 1,150
Hence, the required number is 1,150.
Worksheet on Math Problem Answers
Unsolved Questions:
1. Fahrenheit temperature F is a linear function of Celsius temperature C. The ordered pair (0, 32) is an ordered pair of this function because 0°C is equivalent to 32°F, the freezing point of water. The ordered pair (100, 212) is also an ordered pair of this function because 100°C is equivalent to 212° F, the boiling point of water.
2. A sports field is 300 feet long. Write a formula that gives the length of x sports fields in feet. Then use this formula to determine the number of sports fields in 720 feet.
3. A recipe calls for 2 1/2 cups and I want to make 1 1/2 recipes. How many cups do I need?
4. Mario answered 30% of the questions correctly. The test contained a total of 80 questions. How many questions did Mario answer correctly?
5. Mary’s credit card company charges 16% interest on her outstanding credit card balance each month. Her minimum payment is $20 each month. Mary’s credit card bill is $70 in January. Mary only pays the minimum amount each month, and she does not spend any additional money on her credit card. How long, in months, will it take her to pay off her bill from January?
6. Imagine a can of purple paint that is 3/4 full. This purple paint consists of 40% red paint and 60% blue paint.
Part A : A painter decides to fill the remaining 1/4 of the can with red paint and mixes everything together thoroughly. What percentage of the new mixture is blue paint?
Answer:_________________
Part B: If the painter had chosen to fill the remaining 1/4 of the can with blue paint instead of red paint and mixed it thoroughly, what percentage of the new mixture would be blue paint?
Answer:_________________
7. Brandon has skittles and M&M's in his candy jar in a ratio of 3:5. His little sister Paige comes home from school one day and when Brandon isn't there she eats 1/3 of the skittles. If there are 56 pieces of candy in the jar after Paige eats the skittles, how many M&M's are in the jar?
● Word Problems on Speed Distance Time
● Algebra Word Problems – Money
First Learn.com Best place to learn Math, Science and English.
From Math Problem Answers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
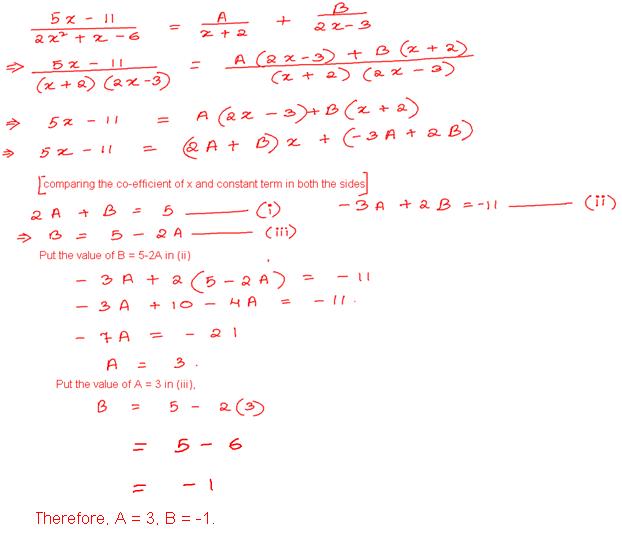



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.