Math Word Problems

Practice various types of math word problems. These activities in math will help the students to understand the different facts of each problem that are useful to translate the information of the questions in the steps and find exact answers of all the questions.

Math Word Problems:

1. Two cities are 1580 miles apart. A plane leaves one of them traveling towards the other at an average speed o 400 mile per hour. At that time a plane leaves the other traveling towards the first at an average speed of 390 miles per hr. How long will it take them to meet?

Answer: 2 hours

2. How much pure acid is in 180 milliliters of a 15% solution?

Answer: 117 ml

3. A table is three times as long as it is wide. If it were 5ft shorter and 5 ft wider it would be square (with all sides equal). How long and how wide is the table?

Answer: Length 15, Width 5

4. Nico is saving money for his college education. He invests some money at 9% and 800 less than that amount @ 6%. The investments produced a total f $222 interest in 1 yr. How much did he invest at each rate?

Answer: $1800 at 9% and $1000 at 6%

5. I had $1.60 in dimes and nickels and had four more dines then nickels. How many of both would I have?

Answer: Nickels 8, Dimes 12

6. How many litters of a 60% acid solution must be mixed with a 25¬id solution to get a 315L of a 50% acid?

Answer:

7. A Dr. Wishes to mix a solution that is 7% monoxide. She has on hand 60 ml of a 6% solution ad wishes to add 9% solution to obtain the desired 7% solution she should add ___ ML

Answer:

8. When 1 is added to the difference between four time’s number and 9, the result is greater than 13 added to 3 times the number. Find all such numbers.

Answer:

9. Randy has $15,000 that he would like to invest. He has a choice of two interest paying bonds, one offering a 4% annual interest and the other paying 8% annual interest. He would like to earn $760 in interest in one year using both types of bonds that he can put towards his vacation. How much money should he invest in each bond?

Answer: $11000 at 4% and $4000 at 8%

10. An elementary school teacher wishes to use 17 feet of scalloped border to enclose a rectangular region on her bulletin board. What is the maximum area that she can enclose with the border?

Answer:

11. The expression 10,000 – 1,000t can be used to calculate the tax value in dollars of a farm tractor that is t years old. How old will the tractor be when its tax value reaches zero?
(a) 12 yr old, (b) 11 yr old, (c) 10 yr old, (d) 13 yr old

Answer: (c) 10 years

12. The total cost of a video game was $42.39. This included 6% sales tax. Find the price without sales tax.

Answer: $ 39.99 (Approx)

13. Clear-water High School expects a 41% increase in enrollment next year. There are 1850 students enrolled this year. How many students will the school gain? What is the expected enrollment next year?

Answer: School gain 1632 students and expected enrollment next year = 2109

14. A fair die is tossed once. Which event is more likely, "the number showing is divisible by three" or "the number showing is even"?

Answer: 6

15. An electric clock was stopped by a power failure. What is the probability that the minute hand stopped between the following two numerals on the face of the clock? a) 12 and 3 b) 1 and 5 c) 11 and 1

Answer: (a) P(12 and 3) = 1/4, (b) P(1 and 5) = 1/3, (c) P(11 and 1) = 1/6

16. Amy the chicken is tied to one corner of a rectangular barn with a 12 foot rope. If the width of the barn is 8 ft and the length is 2 yards, find the area outside the barn in which Amy can travel. Leave pi (Π) in the answer.

Answer:

17. A swimming pool has to be drained for maintenance. The pool is shaped like a cylinder with a diameter of 10m and a depth of 2.2 m . If the water is pumped out of the pool at the rate of 17 m^3 per hour, how many hours does it take to empty the pool? Use the value 3.14 for , and round your answer to the nearest hour.

Answer:

18. The height of a triangle is 4 feet more than 3 times the base. If the area is 32 ft2, find the base and height of the triangle.

Answer: Base = 4 feet, Height = 16 feet.

19. In general, the y-intercept of the function F(x) = a*b^x is the point _____.

Answer: (0, a)

20. The domain of F(x)=(2/3)^x is all negative numbers.

A. True B. False

Answer: B. False

21. For all values of a and b that make F(x) = a * b^x a valid exponential function, the graph always has a horizontal asymptote at y = 0.

A. True B. False

Answer: A. True

22. The range of F(x) = 5 * 2^x is all positive real numbers.

A. True B. False

Answer: A. True

23. The range of the function given below is the set of all positive real numbers greater than 6.

F(x) = 6 + 2^x

A. True B. False

Answer: A. True

24. Graduate students were asked to participate in an evaluation of beers. Each student was given three glasses in a random order. Glasses 1 and 2 both had the same inexpensive local beer, while Glass 3 contained a more expensive imported beer. Students were told that the beer in glass 1 was expensive, but that the beer in glass 2 was not. They were not told anything about glass 3. Students were asked to rate the beers from 1 to 20 with higher ratings indicating better taste. 8 students responses were randomly selected and are presented below. What is your question? Analyze the data to answer the question.

So, the rubric is:

(a) Provide support for a particular approach by exploring whether assumptions underlying parametric/nonparametric/et., assumptions are met.

(b) Surface ideas with techniques (e.g. scatter plot, outliers, etc.) used to analyze the data.3. Define the question and hypotheses ( which of course you will then test).

(c) Identify the key ideas, variables, or issues that frame the research problem

25. A rectangles perimeter is 16 units and its area is 11 square units. please find its exact dimensions.

Answer: Length = 4 + √5 units, Width = 4 - √5 units

26. Astronauts who waked on the moon felt as if they weighed about one sixth of their weight on earth. this is because the weight of an object is determined by the gravitational attraction between the object and the planet (or moon) its on. you can use the following formula to estimate the weight of an object on the surface of any of the planets: gravitational force=GmM/r^2, where G=universal gravitational constant,m=mass of the object, M=mass of the planet, and r=radius of the planet. For a given object, Grandma remain constant, so the force of gravity depends only on the variables named r.

Answer:

27. A store is having a sale on liquid soap and sponges the cost of 6 bottles of soap is 9.12 the coast of 4 sponges is 5.00 what is the total cost of buying 2 bottles of liquid soap and 3 sponges.

Answer:

28. A line contains the points(a, b) and ( a+3, b+3). Find the slope of the line.

Answer: Slope = 1

29. Put the following list of real numbers in order from LEAST to GREATEST. Make sure you show all the steps you took to get to your final answer. -√64 ,-7/2, 3.3, √10, 27/3

Answer:  -√64, -3.5, √10, 3.3, 27/3

30. Johnathon and Talia simplified the following expression on their Algebra 1 midterm: 7 - 2(x - 5).

Answer: Johnathon's work --- Correct Process

31. What is the sales tax and total price of an item that is $45.69 if the sales tax is 7.5 %?

a. sales tax = $3.00; total price = $50.00

b. sales tax = $3.40; total price = $49.09

c. sales tax = $3.43; total price = $49.12

d. sales tax = $3.42; total price = $49.11

Answer: c. sales tax = $3.43; total price = $49.12

32. Kate earns a weekly allowance of $12. How much money will she earn in 8 weeks? Do not enter $.____ dollars

Answer: $ 96

33. A table is shaped like a square and has an area of 100 square feet. Find the length of one side of the table.____ feet

Answer: 10 feet.

34. Juan bought n video games. Write an expression to show the total cost of the games if each game cost $16. Do not enter $ in your answer.

Answer: Total cost f(n) = 16n

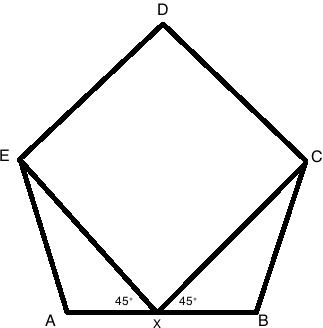
35. A sandpit in the shape of a pentagon ABCDE is to be built in such a way that each of its sides are of equal length, but its angles are not all equal. The pentagon is symmetrical about DX, where X is the midpoint of AB. The angle AXE and BXC are both 45 degrees and each side is 2m long.

(a) Find angle XEA.

(b) Find the length of EX.

(c) How much sand is required if the sandpit is 30 cm deep?

Give your answer to three decimal place.

36. An aircraft takes off from an airstrip and then flies for 16.2 km on a bearing of 066 degrees true. The pilot then makes a let turn of 88 degrees and flies for a further 39.51 km on this course before deciding to return to the airstrip. (a) Through what angle must the pilot turn to return to the airstrip? (b) How far will the pilot have to fly to return to the airstrip?

37. Gracie decided to rent a limo for her wedding. The Bedazzled Limo Com- pany charges a $50 gas fee, $56.48 per hour to rent the limo and requires a tip of 20% on the total price of the rental (so 20% of the total cost of the rental). The Wedding Bell Limo Company charges $68.36 per hour and requires a 25% tip to the driver. For how long of a rental will the hourly cost be the same? (Round to the nearest half hour).

38. Wolf Problem Naturalists find that the population of wolves varies sinusoidally with time on a particular land. After 2.5 years of keeping records, a maximum number of wolves, 1100, was recorded. After 5.2 years, aminimum number of wolves, 300, were recorded.

a. Draw a neat sketch of a graph that models this situation for the first 16 years. Label your axes.

b. Derive an equation expressing the number of wolves, W, as a function of time.

c. Predict the population of wolves in 7 years after keeping records? In 9 years? In 15 years? In 56.5
years?

d. What are the first 4 times (to the nearest hundredth of a year) after keeping records that there are
1000 wolves on the island?

Answers for the different types of math word problems are given below to check the exact answers of the above math questions.

39. Researchers find that the mongoose population is periodic and varies sinusoidally with time. Records were kept beginning with t = 0 years. A minimum number of 500 mongooses occurred when t = 3 years. The next maximum of 1700 mongooses occurred when t = 7 years.

a. Sketch a graph of this sinusoid. Be sure to label the axes on the graph.

b. Write an equation describing the mongoose population P as a function of the time elapsed, t.

c. Mongoose are placed on the endangered species list if the population falls below 900. What are the first two values of t for which this happens?

d. Without using a calculator, how many times does the mongoose population peak in the first 75 years?

Related Concepts

● Math Questions Answers
● Help with Math Problems
● Answer Math Problems
● Math Problem Solver
● Math Unsolved Questions
● Math Questions
● Math Word Problems
● Word Problems on Speed Distance Time
● Algebra Word Problems – Money

Math Problem Answers Index

From Math Word Problems to HOME PAGE