Matrix

A rectangular array of mn elements a_ij into m rows and n columns, where the elements aij belongs to field F, is said to be a matrix of order m × n (or an m × n matrix) over the field F. 

Definition of a Matrix: A matrix is a rectangular arrangement or array of numbers or functions, in the form of horizontal and vertical lines and subject to certain rules of operations.

Matrices are usually denoted by capital letters of the alphabet. 

Very often capital letters A, B, C, ... are used to denote a matrix.

If mn numbers or functions are arranged in the form of a rectangular array Z, having m rows and n columns, then Z is called a m × n matrix.

An m × n matrix is represented in the form

\(Z = \begin{pmatrix} a_{11} & a_{12} & ... & a_{1n}\\ a_{21} & a_{22} & ... & a_{2n}\\ ... & & ... & \\ a_{m1} & a_{m2} & ... & a_{mn} \end{pmatrix}\), or in the form

\(Z = \begin{bmatrix} a_{11} & a_{12} & ... & a_{1n}\\ a_{21} & a_{22} & ... & a_{2n}\\ ... & & ... & \\ a_{m1} & a_{m2} & ... & a_{mn} \end{bmatrix}\)

F is said to be the field of scalars. If, in particular, F be the field of real (complex) numbers, the matrix is said to be a real (complex) matrix. The element aij appearing in the i^th row and j^th column of the matrix is said to be the ij^th element. The matrix is also denoted by the symbol (a_ij)m,n.

Horizontal lines of a matrix are called rows. Vertical lines of a matrix are called columns.

Each number or function a_ij is called its element.

The element of a matrix is usually denoted by a small letter of the alphabet along with two suffixes. The first suffix indicated the number of row and the second one indicated the number of column.

The all numbers or functions aij that is the elements of a matrix are enclosed in brackets [   ].

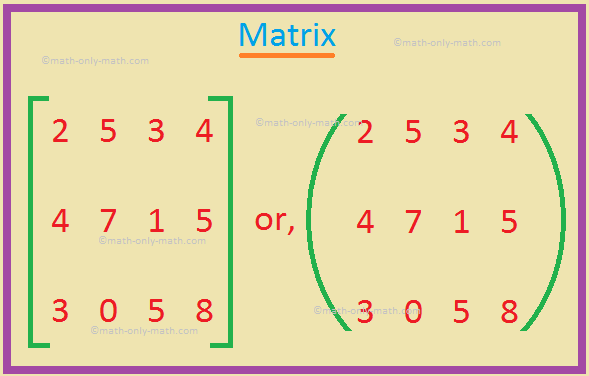
At times, a pair of parenthesis, (  ), are also used to indicate a matrix. For example, the matrix \(\begin{bmatrix} 2 & 5 & 3 & 4\\ 4 & 7 & 1 & 5\\ 3 & 0 & 5 & 8 \end{bmatrix}\) is also expressed as \(\begin{pmatrix} 2 & 5 & 3 & 4\\ 4 & 7 & 1 & 5\\ 3 & 0 & 5 & 8 \end{pmatrix}\)

Let us consider the array \(\begin{bmatrix} 4 & 5\\ 2 & 3\\ 7 & 9 \end{bmatrix}\) of numbers. In this array, there are 3 rows and 2 columns. The element 9 lies in the 3rd row and 2nd column. Similarly, we can fix the position of any other element in the above array. 

● Matrix

• Definition of a Matrix
  
• Order of a Matrix
  
• Position of an Element in a Matrix
  
• Classification of Matrices
• Problems on Classification of Matrices
  
• Square Matrix
• Row Matrix
• Column Matrix
  
• Null Matrix
• Equal Matrices
  
• Identity (or Unit) Matrix
• Triangular Matrix
  
• Addition of Matrices
  
• Addition of Two Matrices
  
• Properties of Addition of Matrices
  
• Negative of a Matrix
  
• Subtraction of Matrices
  
• Subtraction of Two Matrices
  
• Scalar Multiplication of a Matrix
  
• Multiplication of a Matrix by a Number
  
• Properties of Scalar Multiplication of a Matrix
• Multiplication of Matrices
  
• Multiplication of Two Matrices
  
• Problems on Understanding Matrices
  
• Worksheet on Understanding Matrix
  
• Worksheet on Addition of Matrices
  
• Worksheet on Matrix Multiplication
  
• Worksheet on Matrix

10th Grade Math

From Matrix to HOME PAGE