Multiplication of Matrices

Two matrices A and B are said to be conformable for the product AB if the number of columns of A be equal to the number of rows of B.

If A be an m × n matrix and B an n × p matrix then their product AB is defined to be the m × p matrix whose (ij)^th element is obtained by multiplying the elements of the ij^th row of A into the corresponding elements of the j^th column of B and summing the products so obtained.

In other words, if A = (a_ij) _{m, n}, B = (b_ij) _{n, p} then the product AB is a matrix of order m × p and AB = C = (c_ij) _{m, p} where (c_ij) = $\sum_{k = 1}^{n} a_{ik}b_{kj}$, i = 1, 2, 3, ...., m; j = 1, 2, 3, ...., p.  

The ij^th element of the product AB is obtained by multiplying the corresponding elements of the i^throw of A and j^th column of B and adding the products. This sum is called the inner product of the i^th row of A and j^th column of B.  So the (ij)^th element of the product AB is the inner product of the i^th row of A and the j^th column of B.

If the number of columns of A be not equal to number of rows of B, then AB is not defined.

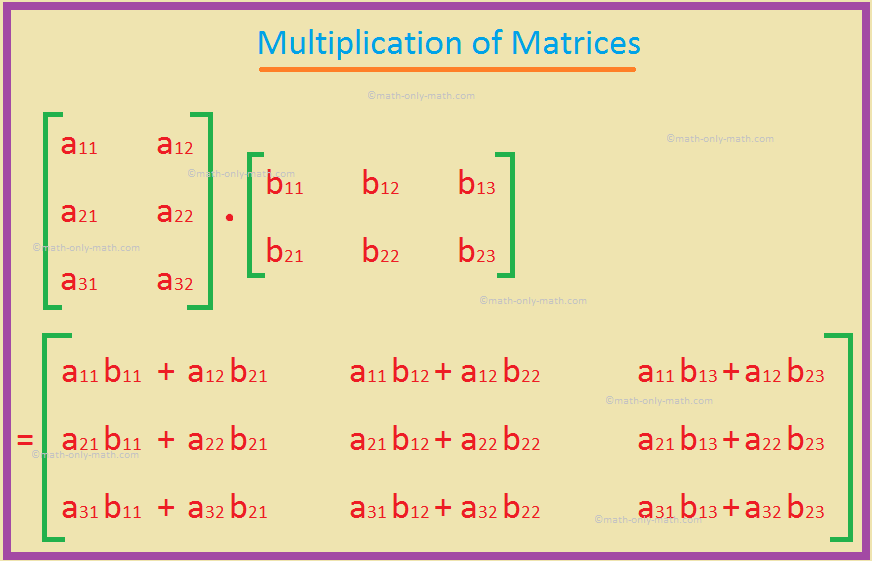
Let A = $\begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22}\\ a_{31} & a_{32} \end{bmatrix}$ and B = $\begin{bmatrix} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23} \end{bmatrix}$

Here we can see that the matrix A has two columns and the matrix B has two rows. Therefore, A and B are conformable for the product AB.

Thus the product of the matrix A and the matrix B = AB = $\begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22}\\ a_{31} & a_{32} \end{bmatrix}$ . $\begin{bmatrix} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23} \end{bmatrix}$

= $\begin{bmatrix} a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} & a_{11}b_{13} + a_{12}b_{23}\\ a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22} & a_{21}b_{13} + a_{22}b_{23}\\ a_{31}b_{11} + a_{32}b_{21} & a_{31}b_{12} + a_{32}b_{22} & a_{31}b_{13} + a_{32}b_{23} \end{bmatrix}$

In the product AB, A is said to be a pre-factor or pre-multiplier and B is said to be a post factor or post-multiplier.

It is obvious that the products AB and BA are two distinct entities. Indeed, one of them may exist while the other may not. In order that both AB and BA should exist, if A be the order of m × n, B must be of order n × m. In this case, however, AB and BA are matrix of different orders. In order that both AB and BA should exist as matrices of the same order, both A and B must be square matrices of the same order.

Note: Matrix multiplication is not commutative. That is, for two matrices A and B, AB ≠ BA, in general.

First of all, if we choose the orders of A and B to be m × n and n × m respectively so that the conformability conditions for both the products AB and BA are satisfied then we observe that the orders of AB and BA are m × m and n × n respectively and therefore AB cannot be equal to BA.

In order that AB and BA may be equal, both of them must be of the same order and this requires that A, B must be square matrices of the same order. However if we choose the order of A and B to be n × n and n × n, then although AB and BA become matrices of the same order, they may not be equal, in general. This can be shown by taking at random.

A = $\begin{bmatrix} 1 & 5\\ 2 & 0 \end{bmatrix}$, B = $\begin{bmatrix} 3 & -1\\ 4 & 6 \end{bmatrix}$

Here AB = $\begin{bmatrix} 23 & 29\\ 6 & -2 \end{bmatrix}$, BA = $\begin{bmatrix} 1 & 15\\ 16 & 20 \end{bmatrix}$.

In some special cases, however, AB = BA.

For example, let A = $\begin{bmatrix} 1 & 2\\ 2 & 3 \end{bmatrix}$, B = $\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}$.

Here AB = $\begin{bmatrix} 1 & 2\\ 2 & 3 \end{bmatrix}$, BA = $\begin{bmatrix} 1 & 2\\ 2 & 3 \end{bmatrix}$.

Definition: Two matrices A and B are said to commute with each other if AB = BA. Since AB = BA, A and B must be square matrices of the same order.

Examples of Commuting Matrices:

1. Let A be a square matrix. Then A commutes with A itself.

2. Let A be a square matrix of order n. Then A commutes with I_n, because A . I_n = I_n . A = A.

3. Let A be a square matrix of order n. Then A commutes with O_n,n, because A. O_n,n = O_n,n . A = O_n,n.

4. Let A be square matrix of order n. Then A commutes with the scalar matrix cI_n, because A . cI_n . A = cI_n . A = cA.

10th Grade Math

From Multiplication of Matrices to HOME