Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Free Math Answers
Free math answers are available on all types of math questions such as basic math, numbers, algebra, logarithm, trigonometry, and pre-calculus homework questions with step-by-step explanations within 24 hours. Math problem solver can work on both basic and advanced concepts. Students can type their question to fill-up the below comment box so that you get your answers within 24 hours.
You can click on the below comment box and submit with the required information along with your homework
questions so that we can help you. Parents and teachers can also contact
us clicking in the below comment box and let us know if you have any doubts so
that we can help you. Math-Only-Math is always with you to help you 24
hours.
In free math answers, these are the questions asked by the students to show it in step-by-step solution.
1. In a group of cows and chickens, the number of legs was 14 more than twice the number of heads. The number of cows was:
(a) 5, (b) 7, (c) 10, (d) 12, (e) 14
Solution:
Let the number of cows be x and their legs be 4x.
Let the number of chicken be y and their legs be 2x.
Total number of legs = 4x + 2y.
Total number of heads = x + y.
The number of legs was 14 more than twice the number of heads.
Therefore, 2 × (x + y) + 14 = 4x + 2y.
or, 2x + 2y + 14 = 4x + 2y.
or, 2x + 14 = 4x [subtracting 2y from both sides].
or, 14 = 4x – 2x [subtracting 2x from both sides].
or, 14 = 2x.
or, x = 7 [dividing by 2 on both sides].
Therefore, the number of cows = 7.
Answer: (b)
2. The roots of the equation ax2 + bx + c = 0 will be reciprocal if:
(a) a = b, (b) a = bc, (c) c = a, (d) c = b, (e) c = ab.
Solution:
Let k be one of the root of the given equation.
According to the problem,
1/k will be the other root of the given equation.
We know that, product of the roots of the equation = c/a.
Therefore, k × 1/k = c/a.
or, 1 = c/a.
or, a = c [multiplying a on both sides].
The roots of the equation ax2 + bx + c = 0 will be reciprocal if a = c.
Therefore, a = c or c = a.
Answer: (c)
3. If 8 ∙ 2x = 5(y+8), then when y = -8, x =
(a) -4, (b) -3, (c) 0, (d) 4, (e) 8
Solution:
8 ∙ 2x = 5(y+8).
or, 8 ∙ 2x = 5(-8+8).
or, 2x = 50.
or, 2x = 1 [anything to the power 0 is 1 then, 50 = 1].
Taking log on both sides,
log 2x = log 1.
or, x log 2 = 0 [since log 1 = 0].
or, x = 0/log 2 [dividing log 2 on both sides].
Therefore, x = 0.
Answer: (c)
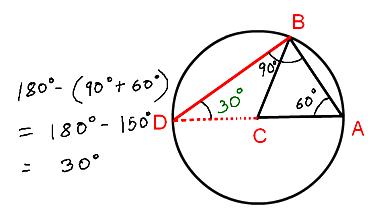
4. A circle of radius 10 inches has its center at the vertex C of an
equilateral triangle ABC and passes through the other two vertices. The
side AC extended through C intersects the circle at D. The number of
degrees of angle ADB is:
(a) 15, (b) 30, (c) 60, (d) 90, (e) 120
Answer: (b)
5. The expression 1 – 1/(1 + √3) + 1/(1 - √3) equals:
(a) 1 - √3, (b) 1, (c) - √3, (d) √3, (e) 1 + √3.
Solution:
6. If x-1 – 1 is divided by x - 1 the quotient is:
(a) 1, (b) 1/(x-1), (c) - 1/(x-1), (d) 1/x, (e) – 1/x
Solution:
x-1 – 1 is divided by (x – 1)
= x-1 – 1 × 1/(x-1)
= 1/x – 1 × 1/(x-1)
= (1 – x/x) × 1/(x-1)
= - (1 – x)/x × 1/(x-1)
= – 1/x [cancel x – 1 from the numerator and denominator].
Answer: (e)
7. The root(s) of 15/(x2 - 4) – 2/(x - 2) = 1 is (are):
(a) -5 and 3, (b) ± 2, (c) 2 only, (d) -3 and 5, (e) 3 only.
Solution:
15/(x2 - 4) – 2/(x - 2) = 1.
15/(x2 - 22) – 2/(x - 2) = 1.
15/(x + 2)(x - 2) – 2/(x - 2) = 1.
[15 – 2(x + 2)]/[(x + 2)(x - 2)] = 1.
[15 – 2x - 4] /[(x + 2)(x - 2)] = 1.
[11 - 2x]/[(x + 2)(x - 2)] = 1.
11 – 2x = (x + 2)(x - 2).
11 – 2x = x2 - 4.
x2 - 4 = 11 – 2x.
x2 + 2x – 4 – 11 = 0.
x2 + 2x – 15 = 0.
x + 5) (x - 3) = 0.
x + 5 = 0 or, x – 3 = 0
x = -5 or, x = 3.
Therefore, x = -5 and 3.
Answer: (a)
8. A 7-in. pizza costs $8 and a 14-in. pizza costs $20. Tommy says
the smaller pizza is a better buy because the larger pizza is twice as
big and more than twice as expensive. Do you agree with his reasoning?
If not, explain why not.
Solution:
No, a pizza looks like a circle.
And we know that area of a circle depends on the radius.
So, we can clearly say that area of a circle is proportional to the square of the diameter.
Similarly, the cost a pizza depends on its area not its diameter.
9. Suppose that Jody drove 80 miles in 2 hours. Dividing 80 by 2
tells us how many miles Jody drove in each hour. The units for this rate
are miles per hour (mi/hr). If we divide 2 by 80 what information would
this give us? Give an interpretation of the rate. What units would be
used for this rate?
Solution:
We know that, speed = distance/time.
When total distance is divided by total time we get the speed.
Here, speed = distance covered in 1 hour.
According to the question,
Total distance 80 miles divided by total time 2 hours = 80/2.
miles/hour = 40 mile/hour.
Therefore, Jody drove 40 miles in 1 hour.
But if we divide total time by total distance then, we get time taken to cover 1 mile.
Similarly, if we divide 2 by 80 then, we get time taken to cover 1 mile.
Therefore, unit used for this case = hours/mile.
10. 19/6 = 4/27. Which method did you use to determine whether this proportion is true or false?
Solution:
19/6 = 4/27.
Cross multiplication:
19 × 27 = 513.
6 × 4 = 24.
We see that 513 are not equal to 24.
Therefore, we determine 19/6 = 4/27 is not proportion so, the answer is false.
11.
On Thursday Mabel handled 90 transactions. Anthony handled 10% more
transactions than Mabel, Cal handled 2/3rds of the transactions that
Anthony handled, and Jade handled 16 more transactions than Cal. How
much transactions did Jade handled?
Solution:
Mabel handled 90 transactions
Anthony handled 10% more transactions than Mabel
Anthony = 90 + 90 × 10%
= 90 + 90 × 0.10
= 90 + 9
= 99
Cal handled 2/3rds of the transactions than Anthony handled
Cal = 2/3 × 99
= 66
Jade handled 16 more transactions than Cal.
Jade = 66 + 16
= 82
Jade handled = 82 transactions.
Answer: 82
12. If a man buys 20 lollipops for $90 and sold them for $2 dollars determine his loss.
Solution:
Cost of 20 lollipops = $90
Sold each lollipop for $2
So he sold 20 lollipops for $(20 × 2) = $40
Loss = $(90 – 40) = $50
Therefore, loss = $ 50.
13 . If C is a whole number, C+1 is a whole number after that. If A is a whole number, what is a whole number before that?
Solution:
We know that the number ‘0’ together with the natural numbers gives us the numbers 0, 1, 2, 3, 4, 5, …………… which are called whole numbers.
If A is a whole number and it is greater than 0 then the whole number before that is A – 1, which will always be a whole number.
Again,
when A is a whole number and it is equal to 0 then the whole number
before that is A – 1 which means 0 – 1 = -1, which is not a whole
number.
Therefore, if A is a whole number then the number before that will not always be a whole number.
14. Solve and leave answer in fraction
- (2-5/4)/9
Solution:
Answer: -1/12
15. Divide the cancelling out all common factors
Solution:
-((1-13/8)/10/24)
Answer: 3/2
16. The annual cost of owning and operating a car, C dollars, is a linear function of the distance, d kilometers, it is driven.
c = md + b
The cost is $4600 for 10 000 km and $9100 for 25 000 km.
(a) Determine the values of m and b.
(b) Write c as a function of d.
Solution:
(a)
c = md + b
The cost is $ 4600 for 10 000 km
4600 = m (10 000) + b
10 000 m + b = 4600
b = -10 000 m + 4600 ------- (i)
The cost is $ 9100 for 25 000 km
9100 = m (25 000) + b
9100 = 25 000 m + b
25 000 m + b = 9100
b = -25 000 m + 9100 --------- (ii)
From equation (i) and (ii) we get;
-10 000 m + 4600 = -25 000 m + 9100
-10 000 m + 25 000 m = 9100 – 4600
15 000 m = 4500
m = 4500/15 000
m = 3/10
m = 0.3
Now, put the value of m = 0.3 in equation (i) we get;
b = -10 000 (0.3) + 4600
b = -3000 + 4600
b = 1600
Answer: m = 0.3 and b = 1600
(b) c = md + b
m = 0.3
b = 1600
c = 0.3d + 1600
Answer: c = 0.3d + 1600
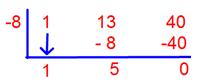
Solution:
We solved the division in both the ways;
(x2 + 13x + 40) ÷ (x + 8) by using synthetic division
Quotient = x + 5
Remainder = 0
OR
(x2 + 13x + 40) ÷ (x + 8) by using long division
Quotient = x + 5
Remainder = 0
Answer: x + 5
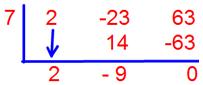
18. Solve using on synthetic division or long division (2x2 - 23x + 63) ÷ (x - 7)
Solution:
We solved the division in both the ways;
(2x2 - 23x + 63) ÷ (x - 7) by using synthetic division,
Quotient = 2x - 9
Remainder = 0
OR
(2x2 - 23x + 63) ÷ (x - 7) by using long division Quotient = 2x - 9
Remainder = 0
Answer: 2x - 9
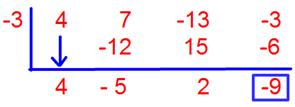
19. Let f(x) = 4x3 + 7x2 – 13x – 3 and g(x) = x + 3. Find f(x)/g(x)
Solution:
f(x) = 4x3 + 7x2 – 13x – 3
g(x) = x + 3
f(x)/g(x) = (4x3 + 7x2 – 13x – 3)/(x + 3)
We solved the division in both the ways;
(4x3 + 7x2 – 13x – 3) ÷ (x + 3) by using synthetic division
Answer:
Quotient = 4x2 – 5x + 2
Remainder = -9
OR
(4x3 + 7x2 – 13x – 3) ÷ (x + 3) by using long division
Answer:
Quotient = 4x2 – 5x + 2
Remainder = -9
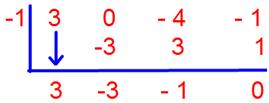
20. Let f(x) = 3x3 - 4x – 1 and g(x) = x + 1. Find f(x)/g(x)
Solution:
f(x) = 3x3 - 4x – 1
g(x) = x + 1
f(x)/g(x) = (3x3 - 4x – 1)/(x + 1)
We first need to rearrange all the terms of the dividend according to descending powers of x. The dividend then becomes 3x3 - 4x – 1, with 3 understood as the coefficient of the first term. No x2 term is there in the polynomial, but we take a zero as a place holder in the x2 position, so the dividend is written as 3x3 + 0x2 - 4x – 1.
We solved the division in both the ways;
(3x3 + 0x2 - 4x – 1) ÷ (x + 1) by using synthetic division
Quotient: 3x2 – 3x – 1
Remainder: 0
OR
No x2 term is there in the polynomial, but we take a zero as a place holder in the x2 position, so the dividend is written as
3x3 + 0x2 - 4x – 1.
(3x3 + 0x2 - 4x – 1) ÷ (x + 1) by using long division
Quotient: 3x2 – 3x – 1
Remainder: 0
Answer: 3x2 – 3x – 1
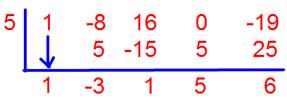
21. Let f(x) = x4 – 8x3 + 16x2 – 19 and g(x) = x - 5. Find f(x)/g(x)
Solution:
f(x) = x4 – 8x3 + 16x2 – 19
g(x) = x – 5
f(x)/g(x) = (x4 – 8x3 + 16x2 – 19)/(x - 5)
We first need to rearrange all the terms of the dividend according to descending powers of x. The dividend then becomes x4 – 8x3 + 16x2 – 19, with 1 understood as the coefficient of the first term. No x term is there in the polynomial, but we take a zero as a place holder in the x position, so the dividend is written as x4 – 8x3 + 16x2 + 0x – 19.
We solved the division in both the ways;
(x4 – 8x3 + 16x2 + 0x – 19) ÷ (x - 5) by using synthetic division
Quotient = x3 - 3x2 + x + 5
Remainder = 6
OR
No x term is there in the polynomial, but we take a zero as a place holder in the x position, so the dividend is written as
x4 – 8x3 + 16x2 + 0x – 19.
(x4 – 8x3 + 16x2 + 0x – 19) ÷ (x - 5) by using long division
Quotient = x3 - 3x2 + x + 5
Remainder = 6
Answer:
Quotient = x3 - 3x2 + x + 5
Remainder = 6
If students have any queries in future regarding any type of questions, please fill-up the below comment box to convey your message, so that we can help you providing free math answers with step-by-step explanation.
From Free Math Answers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
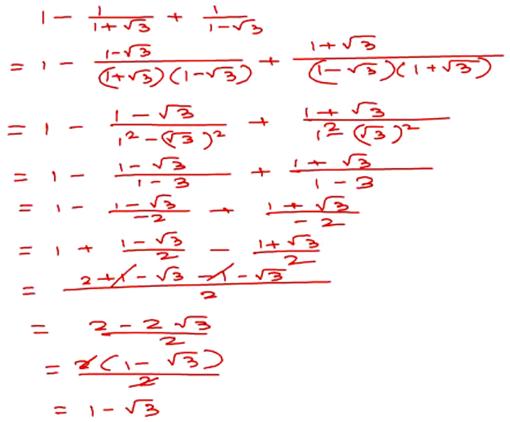
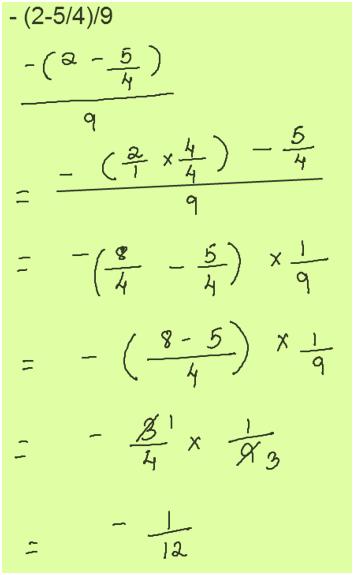
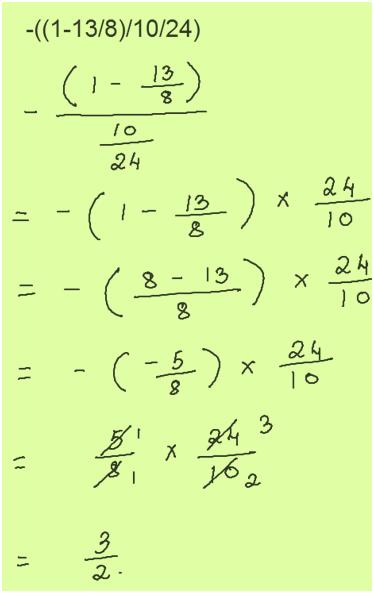
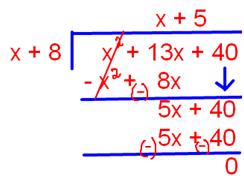
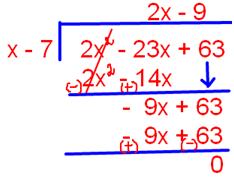





New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.