Addition and Subtraction Together

We will solve the different types of problems involving addition and subtraction together.

To show the problem involving both addition and subtraction, we first group all the numbers with ‘+’ and ‘-‘ signs. We find the sum of the numbers with ‘+’ sign and similarly the sum of all the numbers with ‘-‘ sign and then find the difference.

Some problems require both addition and subtraction to find out their solutions. In those cases, first you have to decide whether to add or subtract,

Here are hints.

• The word problems with 'How many are there in all', "What is the total of, or 'Find the total of', etc., are addition problems.

• The word problems with 'How many are left', 'How many less', etc., are subtraction problems.

Addition and Subtraction Together Video

Subscribe to our YouTube channel for the latest videos, updates, and tips.

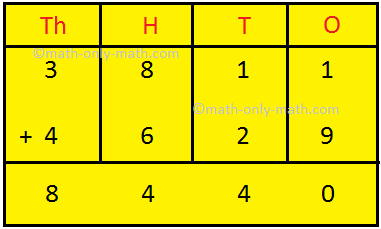
1. Solve 3811 + 4629 – 1821 – 3164

Solution:

Step I: Add the numbers with ‘+’ sign. Step II: Add the numbers with ‘-’ sign. Step III: Subtract the sum of the numbers with ‘-’ sign from the sum of the numbers with ‘+’ sign.

Step 1

Note: If there is no sign before a number it means ‘+’ sign.

Step 2

Step 3

Answer: 3811 + 4629 - 1821 - 3164 = 3455

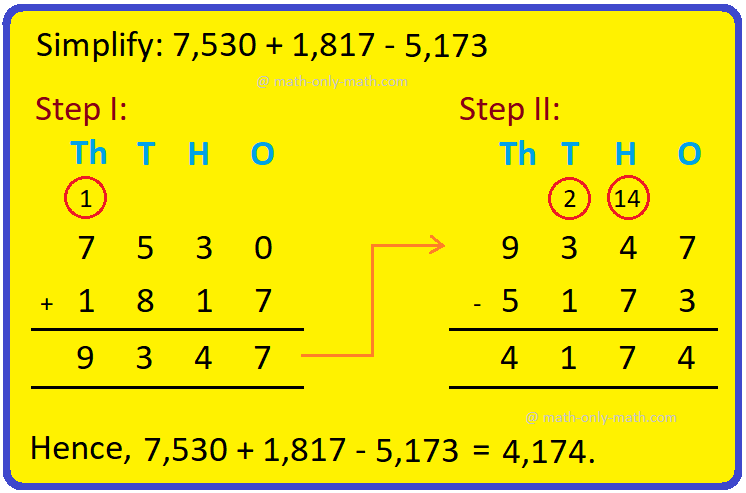
2. Simplify: 7,530 + 1,817 - 5,173

Solution:

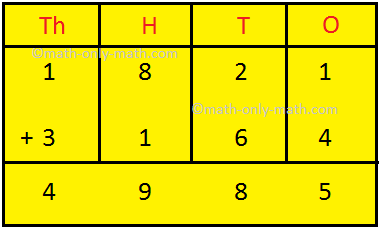
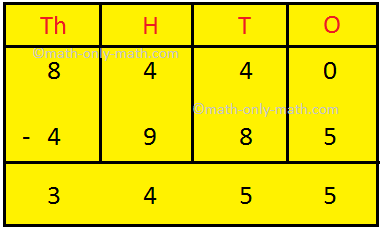
3. Solve: 5,892 - 1,398 + 784 - 2,904

Solution:

Step I:  5,892 - 1,398

Step II: Above difference 4494 + 789

Step III: Above result 5278 - 2904

Therefore, 5,892 - 1,398 + 784 - 2,904 = 2,374

Note: If there is no sign before the first number, its sign is always taken as plus.

Combination of Addition and Subtraction Video

Word Problems on Addition and Subtraction Together:

4. In godown A, there are 41,929 bags of rice and 31930 bags of wheat. In godown B, there are 31,556 bags of rice and 40,999 bags of wheat. Which godown contains more number of bags and by how much?

Godown A Number of bags of rice      =    41929

Number of bags of wheat                  = + 31930

Total number of bags                        =    73859

Godown B Number of bags of rice      =    31556

Number of bags of wheat                  = + 40999

Total number of bags                        =    72555

Total number of bags in godown A - Total number of bags in godown B

                                                      =     73,859 – 72,555

                                                      =     1,304

Therefore, godown A contains 1,304 bags more than that in godown B.

5. Population of California was 12,935,297 in 2007. It increased by 4,534,214 in next five years, but 1,329,417 migrated to Florida, and Georgia. Population of California in 2012 was

(i) 174,695,111

(ii) 16,140,094

(iii) 8,401,083

(iv) 11,605,880

Solution:

Population of California in 2007  =    12,935,297

Increase in population               = +  4,534,214

Increase population                   =   17,469,511

Migrated population                   = -  1,329,417

Hence, final population in 2012   =  16,140,094

So, the option (ii) is correct, which is the required answer

Note: 
We have added 12,935,297 (Population of California in 2007) with 4,534,214 (Population increased by next five years) because, population was increased and subtracted 1,329,417 from 17,469,511 (Increase population) because, population was decreased due to migration.

6. A man set out on a journey of 584 km and completed it in 3 days. He covered 216 km on the first day and 198 km on the second day. How much did he travel on the third day?

Solution:

Therefore, he travelled 170 km on the third day.

Worksheet on Addition and Subtraction Together:

I. Solve the following:

(i) 5406 + 1809 – 3281

(ii) 2805 + 4961 – 1629 - 128

(iii) 3619 + 5410 – 2018 – 3110

(iv) 1529 + 402 + 506 – 1200

Answer:

I. (i) 3934

(ii) 6009

(iii) 3901

(iv) 1237

II. Simplify: (Addition and Subtraction Together)

(i) 3,298 + 6,121 - 1,784

(ii) 5,314 - 2,610 + 5,001

(iii) 5,418 - 3,514 + 4,563

(iv) 5,498 - 4,543 + 2,004

(v) 4, 381 + 4,824 - 2,901

(vi) 9,405 - 6,361 + 1,032 - 2,498

(vii) 5,392 + 1,834 - 2,721 - 780

(viii) 3,001 + 5,123 - 6,123 + 2,89

(ix) Subtract the difference of 8,451 and 3,468 from their sum.

Answer:

II. (i) 7,635

(ii) 7,705

(iii) 6,467

(iv) 2,959

(v) 6,304

(vi) 1,578

(vii) 3,725

(viii) 4,891

(ix) 6,936

Worksheet on Word Problems on Addition & Subtraction Together:

III. Ron bought a plot for $2,55,000. He constructed a house spending $5,45,328 and sold it for $10,45,350. What is his gain?

Answer:

III. $2,45,022

IV. Mr. X has a deposit of $3,68,750. Mr. Y has $7592 less than Mr. X. Mr. Z has $50,490 more than Mr. X. Calculate the deposit of Mr. Y and Mr. Z.

Answer:

IV. Mr. Y : $ 361158

      Mr. Z. : $ 419240

V. A post man delivered 65 packets of gift and 137 letters during the week. How many deliveries should he do more to reach 275 deliveries?

Answer:

V. 73 deliveries.

VI. A stationery shopkeeper sold 345 black pens and 462 blue pens. If he had 976 pens, how many pens were left unsold?

Answer:

VI. 169 pens.

VII. Alexander bought 384 bottles of orange squash and 297 bottles of lemon squash. He sold 424 bottles of squash. How many bottles were left unsold?

Answer:

VII. 257 bottles

4th Grade Math Activities

From Addition and Subtraction Together to HOME PAGE