Subscribe to our YouTube channel for the latest videos, updates, and tips.

Expanded Form of a Number

Q: 1. What is the expanded form of a number?

Answer: A number written as the sum of the place values of its digits, is said to be in expanded form of a number.

Q: 2. What is the short form of a number?

Answer: The number written in standard form is said to be in short form

Q: 3. What is the expanded form of 468?

Answer: The expanded form of the number 468 = 400 + 60 + 8

We know that the number written as sum of the place-values of its digits is called the expanded form of a number.

Standard Form		Expanded Form
20,37,81,405	=	20,00,00,000 + 0 + 30,00,000 + 7,00,000 + 80,000 + 1,000 + 400 + 0 + 5

In expanded form of a number, the number is shown according to the place values of its digits.

This is shown here:

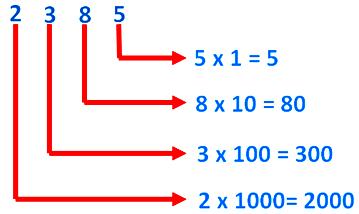
In 2385, the place values of the digits are given below:

$Standard Form and Expanded Form$

Hence, 2385 = 2000 + 300 + 80 + 5

Thus, 2000 + 300 + 80 + 5 is the expanded form of 2385.

Again,

2,55,109	=	2,00,000 + 50,000 + 5,000 + 100 + 0 + 9
Standard Form		Expanded Form

Expanded form of a Number Video

Subscribe to our YouTube channel for the latest videos, updates, and tips.

Expanded Notation

The digits of the numerals 394381, 163845, 583927 are entered in the place value chart as given below.

Lakhs 100000	Ten thousands 10000	Thousands 1000	Hundreds 100	Tens 10	Ones 1
3	9	4	3	8	1
1	6	3	8	4	5
5	8	3	9	2	7

(i) What is the expanded form of the number 394381?

394381 = 3 lakhs + 9 ten thousands + 4 thousands + 3 hundreds +

8 tens + 1 one

= 3 × 100000 + 9 × 10000 + 4 × 1000 + 3 × 100 + 8 × 10 +

1 × 1

= 300000 + 90000 + 4000 + 300 + 80 + 1

(ii) What is the expanded form of the number 163845?

163845 = 1 lakhs + 6 ten thousands + 3 thousands + 8 hundreds +

4 tens + 5 ones

= 1 × 100000 + 6 × 10000 + 3 × 1000 + 8 × 100 + 4 × 10 +

= 5 × 1

= 100000 + 60000 + 3000 + 800 + 40 + 5

(iii) What is the place value of all the digits of number 583927?

Digit			Place Value
5	5 lakhs	→	5 × 100000 = 500000
8	8 ten thousands	→	8 × 10000 = 80000
3	3 thousands	→	3 × 1000 = 3000
9	9 hundreds	→	9 × 100 = 900
2	2 tens	→	2 × 10 = 20
7	7 ones	→	7 × 1 = 7

Given the expanded form of a number, we can also write the numeral in the standard form.

500000 + 80000 + 3000 + 900 + 20 + 7

= 583927

Expanded form of a number to standard form.

(iv) 3000 + 200 + 40 + 8 = 3248

(v) 7 ten thousands + 4 thousands + 2 hundreds + 3 tens + 8 ones

= 74238

2-Digit Numbers in Expanded From Video

3-Digit Numbers in Expanded From Video

4-Digit Numbers in Expanded From Video

5-Digit Numbers in Expanded From Video

6-Digit Numbers in Expanded From Video

Subscribe to our YouTube channel for the latest videos, updates, and tips.

Solved Examples on Expanded Form of a Number:

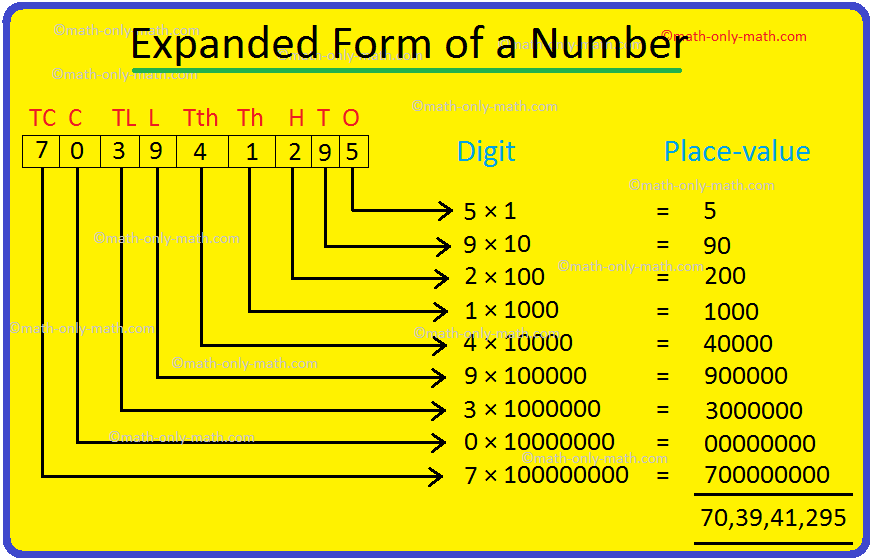
1. Write the expanded form for the number 70,39,41,295.

Solution:

$Expanded Form of a Number$

Therefore, the expanded form of the number 70,39,41,295 is 70,00,00,000 + 00000000 + 3000000+ 900000 + 40000 + 1000 + 200 + 90 + 5.

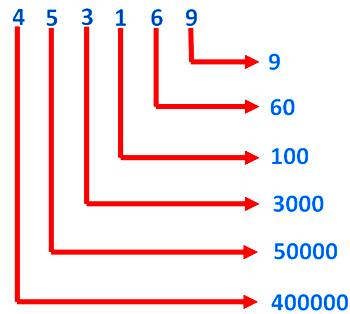
2. Find the expanded form of 453169.

Solution:

Place values of digits 453169

$Find the Expanded Form of a Number$

So, 453169 = 400000 + 50000 + 3000 + 100 + 60 + 9

3. Write the number in figures and then in words for the following expanded form:

(i) 80000 + 8000 + 500 + 50 + 7

Solution:

80000 + 8000 + 500 + 50 + 7

= 88557 (in figures)

Eighty eight thousand five hundred fifty seven (in words)

(ii) 100000 + 30000 + 2000 + 10 + 6

Solution:

100000 + 30000 + 2000 + 10 + 6 = 132016 (in figures)

One hundred thirty two thousand sixteen (in words)

We can write the expanded form of numbers in different ways.

4. Write in expanded form:

(i) 28369

Write as:

(a) 20000 + 8000 + 300 + 60 + 9

(b) 2 × 10000 + 8 × 1000 + 3 × 100 + 6 × 10 + 9 × 1

(ii) 419,247

Write as:

(a) 400000 + 10000 + 9000 + 200 + 40 + 7

(b) 4 × 100000 + 1 × 10000 + 9 × 1000 + 2 × 100 + 4 × 10 + 7 × 1

Writing a numeral as the sum of the place values of all its digits is called the expanded form of that numeral.

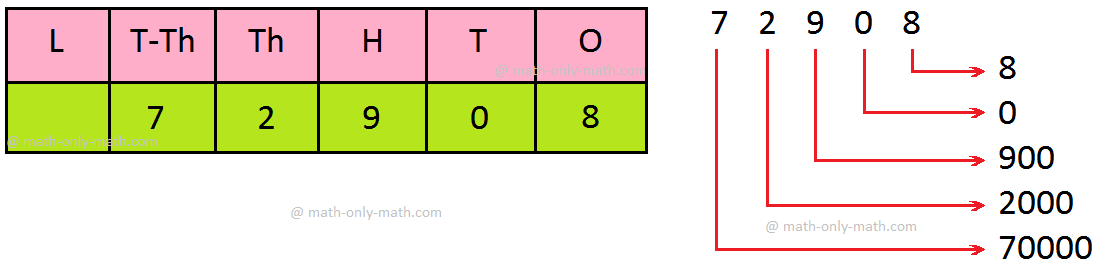
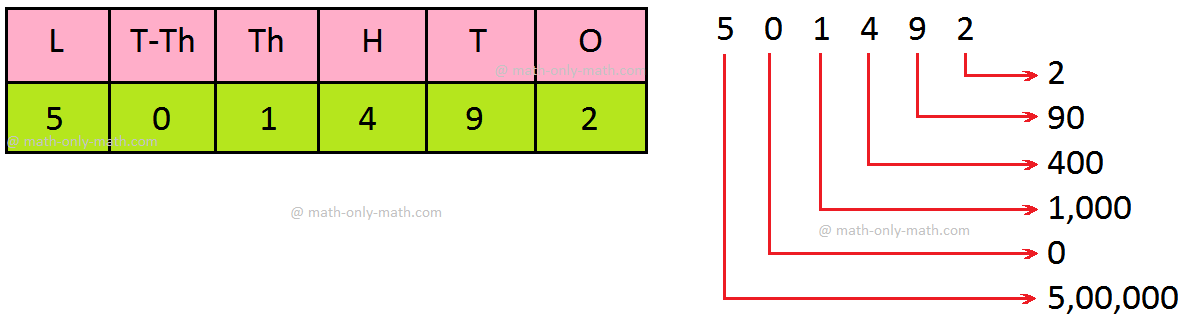
5. Write (i) 72,908; (ii) 5,01,492 in the expanded form.

Solution:

Write the given numbers in the place-value chart.

(i) 72,908

$Expanded Form - Place Value Chart$

Thus, 72, 90870,000 + 2,000 + 900 + 0 + 8

(ii)

$Expanded Form and Place Value Chart$

Thus, 5,01,492 = 5,00,000 + 0 + 1,000 + 400 + 90 + 2

= 5,00,000 + 1,000 + 400 + 90 + 2

Numbers Beyond One Lakh

1 lakh	= 10⁵	= 100000
2 lakh	= 5 × 10²	= 200000
3 lakh	= 5 × 10³	= 300000
4 lakh	= 5 × 10⁴	= 400000
5 lakh	= 5 × 10⁵	= 500000
6 lakh	= 6 × 10⁵	= 600000
7 lakh	= 7 × 10⁵	= 700000
8 lakh	= 8 × 10⁵	= 800000
9 lakh	= 9 × 10⁵	= 900000
10 lakh	= 10 × 10⁵	= 1000000

Note: There are 7 digits in ten lakhs.

Therefore the seventh place is called ten lakhs place.

Expanded Form of Large Numbers

Expanded Form (In Indian system)

We already know how to express a number in the expanded form. We can also express the larger number written in the Indian system or International system in the expanded form.

For Example.

1. Write the expanded form of the number 34,78,35,334 in the Indian system.

Solution:

In the Indian system the number 34,78,35,334 can be written in the expanded form as:

30,00,00,000 + 4,00,00,000 + 70,00,000 + 8,00,000 + 30,000 + 5,000 + 300 + 30 + 4.

2. Write the expanded form of the number 748,301,413,119 in the International system.

Solution:

In the International system the number 748,301,413,119 can be written in the expanded form as:

700,000,000,000 + 40,000,000,000 + 8,000,000,000 + 300,000,000 + 1,000,000 + 400,000 + 10,000 + 3,000 + 100 + 10 + 9.

Worksheet on Expanded Form of a Number:

I. Write the given numbers in expanded form:

(i) 617 = _____ + _____ + _____

(ii) 319 = _____ + _____ + _____

(iii) 286 = _____ + _____ + _____

(iv) 939 = _____ + _____ + _____

(v) 677 = _____ + _____ + _____

(vi) 918 = _____ + _____ + _____

(vii) 328 = _____ + _____ + _____

(viii) 520 = _____ + _____ + _____

(ix) 647 = _____ + _____ + _____

(x) 474 = _____ + _____ + _____

Answer:

I. (i) 600 + 10 + 7

(ii) 300 + 10 + 9

(iii) 200 + 80 + 6

(iv) 900 + 30 + 9

(v) 600 + 70 + 7

(vi) 900 + 10 + 8

(vii) 300 + 20 + 8

(viii) 500 + 20 + 0

(ix) 600 + 40 + 7

(x) 400 + 70 + 4

II. Write the expanded form for the given numbers:

(i) 7,12,306

(ii) 8,07,392

(iii) 6,44,895

(iv) 3,73,737

(v) 9,22,005

Answers:

II. (i) 7,00,000 + 10,000 + 2,000 + 300 + 0 + 6

(ii) 8,00,000 + 0 + 7,000 + 300 + 90 + 2

(iii) 6,00,000 + 40,000 + 4,000 + 800 + 90 + 5

(iv) 3,00,000 + 70,000 + 3,000 + 700 + 30 + 7

(v) 9,00,000 + 20,000 + 2,000 + 0 + 0 + 5

III. Write the given number in standard form:

(i) 30,000 + 4,000 + 700 + 2

(ii) 2,00,000 + 80,000 + 4,000 + 800 + 50

(iii) 6,00,000 + 40,000 + 4,000 + 800 + 90 + 5

(iv) 8,00,000 + 10,000 + 6,000 + 200 + 50 + 7

(v) 1,00,000 + 20,000 + 1,000 + 200 + 10 + 2

(vi) 9,00,000 + 2

Answers:

III. (i) 34702

(ii) 2,84,850

(iii) 6,44,895

(iv) 8,16,257

(v) 1,21,212

(vi) 9,00,002

IV. Rearrange and write the number:

(i) 5 ones 6 tens 1 hundred

(ii) 7 hundreds 9 ones 1 ten

(iii) 3 tens 5 hundreds 6 ones

(iv) 8 ones 9 tens 2 hundreds

(v) 4 hundreds 6 ones 7 tens

(vi) 2 tens 3 hundreds 6 ones

_____ _____ _____

Answer:

(i) 1 hundred 6 tens 5 ones

(ii) 7 hundreds 1 ten 9 ones

(iii) 5 hundreds 3 tens 6 ones

(iv) 2 hundreds 9 tens 8 ones

(v) 4 hundreds 7 tens 6 ones

(vi) 3 hundreds 2 tens 6 ones

165

719

536

298

476

326

V. Circle the correct one

(i) 9 hundreds 2 tens 3 ones

(ii) 6 hundreds 0 tens 1 one

(iii) 3 hundreds 6 tens 3 ones

(iv) 2 hundreds 2 tens 1 one

(v) 5 hundreds 8 tens 4 ones

(vi) 9 hundreds 8 tens 0 ones

932 923 329

106 601 610

363 336 633

212 221 122

854 584 485

980 908 809

Answer:

(i) 923

(ii) 601

(iii) 363

(iv) 221

(v) 584

(vi) 980

VI. Write the following numbers in the expanded form in three different ways as shown in the examples.

(i) 61,052

61,052 - 6 ten thousands + 1 thousand + 0 hundreds + 5 tens + 2 ones

- 6 × 10000 + 1 × 1000 + 0 × 100 + 5 × 10 + 2× 1

- 60000 + 1000 + 0 + 50 + 2

(ii) 1, 99, 099

(iii) 2,80,476

(iv) 3,67,814

(v) 8,31, 879

VII. Write the correct numbers in the blanks:

(i) _____ + 800 + 30 = 5,00,832

(ii) 1,00,000 +_____ + 5 = 1,10,005

(iii) _____ lakh + 2 ten thousands + 3 thousands + 7 hundreds + 6 tens + 5 ones = 9,23,465

(iv) 60,000 + _____ + 500 + 70 + 2 = 62,572

(v) _____ + 900 + 40 + 9 = 8,949

Answer:

VII. (i) 5,00,000

(ii) 10,000

(iii) 9

(iv) 2,000

(v) 8,000

VIII. Fill in the blanks. One has been done for you.

(i) 356 = __3__ hundreds __5__ tens and __6__ ones

(ii) 593 = _____ hundreds _____ tens and _____ ones

(iii) 639 = _____ hundreds _____ tens and _____ ones

(iv) 765 = _____ hundreds _____ tens and _____ ones

Answer:

VIII. (ii) 5 hundreds; 9 tens; 3 ones

(iii) 6 hundreds; 3 tens; 9 ones

(iv) 7 hundreds; 6 tens; 5 ones

IX. Write the expanded form of 3-digit numbers. One has been done for you.

(i) 645 = _600_ + __40__ + __5__

(ii) 397 = _____ + _____ + _____

(iii) 702 = _____ + _____ + _____

(iv) 631 = _____ + _____ + _____

Answer:

IX. (ii) 300 + 90 + 7

(iii) 700 + 0 + 2

(iv) 600 + 30 + 1

X. Write the 3-digit numbers in short form as shown.

(i) 100 + 20 + 6 = __126__

(ii) 900 + 20 + 9 = _____

(iii) 600 + 60 + 6 = _____

(iv) 400 + 0 + 3 = _____

(v) 300 + 40 + 5 = _____

(vi) 800 + 70 + 4 = _____

(vii) 700 + 70 + 8 = _____

(viii) 900 + 20 + 0 = _____

X. (ii) 929

(iii) 666

(iv) 403

(v) 345

(vi) 874

(vii) 778

(viii) 920

XI. Express in expanded form.

(i) 49,38,268

(ii) 29,17,25,219

(iii) 76,09,25,011

(iv) 524,698,432,381

(v) 94,308,409,002

(vi) 174,325,946,791

Answer:

XI. (i) 40,00,000 + 9,00,000 + 30,000 + 8,000 + 200 + 60 +8

(ii) 20,00,00,000 + 9,00,00,000 + 10,00,000 + 7,00,000 + 20,000 + 5,000 + 200 + 10 + 9

(iii) 70,00,00,000 + 6,00,00,000 + 9,00,000 + 20,000 + 5,000 + 10 + 1

(iv) 500,000,000,000 + 20,000,000,000 + 4,000,000,000 + 600,000,000 + 90,000,000 + 8,000,000 + 400,000 + 30,000 + 2,000 + 300 + 80 + 1

(v) 90,000,000,000 + 4,000,000,000 + 300,000,000 + 8,000,000 + 400,000 + 9,000 + 2

(vi) 100,000,000,000 + 70,000,000,000 + 4,000,000,000 + 300,000,000 + 20,000,000 + 5,000,000 + 900,000 + 40,000 + 6,000 + 700 + 90 + 1

1. What is the expanded form of a number?

Answer:

A number written as the sum of the place values of its digits, is said to be in expanded form of a number.

2. What is the short form of a number?

Answer:

The number written in standard form is said to be in short form

3. What is the expanded form of 468?

Answer:

The expanded form of the number 468 = 400 + 60 + 8

You might like these

Multiplication of a Number by a 3-Digit Number |3-Digit Multiplication
In multiplication of a number by a 3-digit number are explained here step by step. Consider the following examples on multiplication of a number by a 3-digit number: 1. Find the product of 36 × 137
Indian Numbering System | Ones Period | Thousands Period |Lakhs Period
In the Indian numbering system, we use different periods like ones, thousands, lakhs, crores, etc. Suppose, let us understand the Indian system by using number 1: ones (1), tens (10), hundreds (100)
Worksheet on Adding 4-Digit Numbers with Regrouping |
In worksheet on adding 4-digit numbers with regrouping we will solve the addition of 4-digit numbers with regrouping or with carrying, 4-digit vertical addition, arrange in columns and add and missing numbers in 4-digit addition.
Worksheet on Word Problems on Addition and Subtraction Together | Ans
In 4th grade worksheet on word problems on addition and subtraction, all grade students can practice the questions on word problems based on addition and subtraction. This exercise sheet on
Division of Four-Digit by a One-Digit Numbers | Worksheet with Answer
In division of four-digit by a one-digit numbers are discussed here step by step. How to divide 4-digit numbers by single-digit numbers?
Division by Two-Digit Numbers | Knowledge of Estimation | Division
In division by two-digit numbers we will practice dividing two, three, four and five digits by two-digit numbers. Consider the following examples on division by two-digit numbers: Let us use our knowledge of estimation to find the actual quotient. 1. Divide 94 by 12
Rounding off Numbers | Nearest Multiple of 10 | Nearest Whole Number
Rounding off numbers are discussed here, where we need to round a number. (i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left. (ii) If we purchase another thing and its cost is $15.78. The cost is rounded up
Examples on the Formation of Greatest and the Smallest Number |Example
In examples on the formation of greatest and the smallest number we know that the procedure of arranging the numbers in ascending and descending order.
Check for Subtraction and Addition | Checking Subtraction | Problems
We will learn to check for subtraction and addition answers after solving. Difference of two numbers is correct when the sum of the subtrahend number and the difference is equal to the minuend.
Dividing 3-Digit by 1-Digit Number Video | Long Division | Worksheet
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit number. I: Dividing 3-digit Number by 1-Digit Number without Remainder:

Related Concept

4th Grade Math Activities

From Expanded form of a Number to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

Facebook X Pinterest WhatsApp Messenger

[?]Subscribe To This Site

$XML RSS$

Recent Articles

Speed Distance and Time | Relation between Speed Distance and Time
May 21, 25 12:58 PM
Speed is defined as the distance covered per unit time. Speed = (Distance Travelled)/(Time Taken) Or, S = D/T. Speed also requires a unit of measurement. If the distance is in kilometres
Read More
Math Problem Answers | Solved Math Questions and Answers | Free Math
May 21, 25 12:45 PM
$Partial fraction$
Math problem answers are solved here step-by-step to keep the explanation clear to the students. In Math-Only-Math you'll find abundant selection of all types of math questions for all the grades
Read More
Test of Divisibility | Divisibility Rules| Divisible by 2, 3, 5, 9, 10
May 21, 25 10:29 AM
The test of divisibility by a number ‘x’ is a short-cut method to detect whether a particular number ‘y’ is divisible by the number ‘x’ or not. Test of divisibility by 2: A number is divisible by 2
Read More
Divisible by 7 | Test of Divisibility by 7 |Rules of Divisibility by 7
May 21, 25 10:17 AM
$Divisible by 7$
Divisible by 7 is discussed below: We need to double the last digit of the number and then subtract it from the remaining number. If the result is divisible by 7, then the original number will also be
Read More
Average Word Problems | Worksheet on Average Questions with Answers
May 20, 25 05:40 PM
In average word problems we will solve different types of problems on basic concept of average. 1. Richard scored 80, 53, 19, 77, 29 and 96 runs in 6 innings in a series. Find the average runs scored…
Read More

E-mail Address

First Name

Then Don't worry — your e-mail address is totally secure. I promise to use it only to send you Math Only Math.