Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
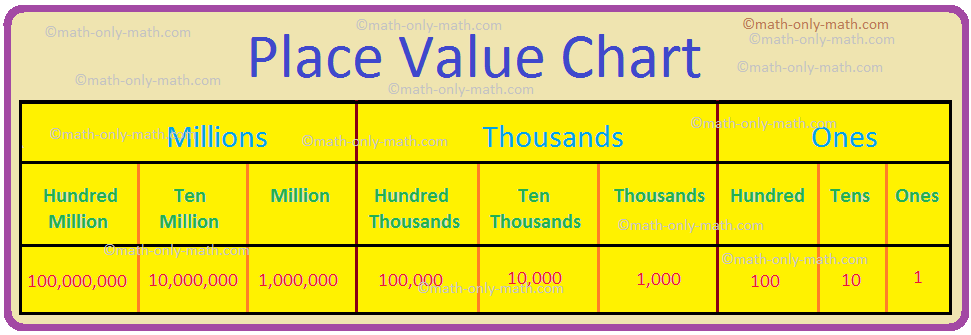
Place Value Chart
In place value chart, the digits are grouped in the threes in a big
number. The number is read from left to right as ………. billion ……….
million ……….. thousands ……….. ones.
The place value chart of the International System is given below:
100,000 = 100 thousand
1,000,000 = 1 million
10,000,000 = 10 millions
100,000,000 = 100 millions
Whole numbers can be represented on the place-value chart.
The numbers 702845 and 360400295 are represented on the place-value chart.
We can expand these numbers as:
702845 = 7 × 100000 + 2 × 1000 + 8 × 100 + 4 × 10 + 5 × 1
360400295 = 3 × 100000000 + 6 × 10000000 + 4 × 100000 + 2 × 100 + 9 × 10 + 5 × 1
In 702845:
Place value of 7 is 7 × 100000 = 700000 and the place is hundred thousand.
Place value of 2 is 2 × 1000 = 2000 and the place is thousands.
Place value of 8 is 8 × 100 = 800 and the place is hundreds.
Place value of 4 is 4 × 10 = 40 and the place is tens.
Place value of 5 is 5 × 1 = 5 and the place is ones.
In 360400295:
Place value of 3 is 3 × 100000000 = 300000000 and the place is hundred million.
Place value of 6 is 6 × 10000000 = 60000000 and the place is ten million.
Place value of 4 is 4 × 100000 = 400000 and the place is hundred thousand.
Place value of 2 is 2 × 100 = 200 and the place is hundred.
Place value of 9 is 9 × 10 = 90 and the place is tens.
Place value of 5 is 5 × 1 = 5 and the place is ones.
Note:
The place value of digit 0 at any place is 0.
Let’s read the numbers by observing the place value chart;
218705 – The number is read as 218 thousands 705.
It is written as 218,705 (using comma).
42156 – The number is read as 42 thousands 156.
It is written as 42,156 (using comma).
25374821 – The number is read as 25 million 374 thousands 821.
It is written as 25,374,821 (using comma).
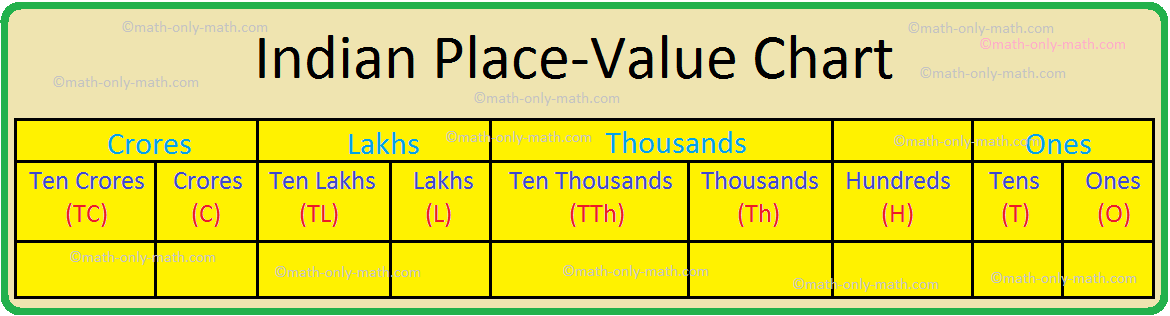
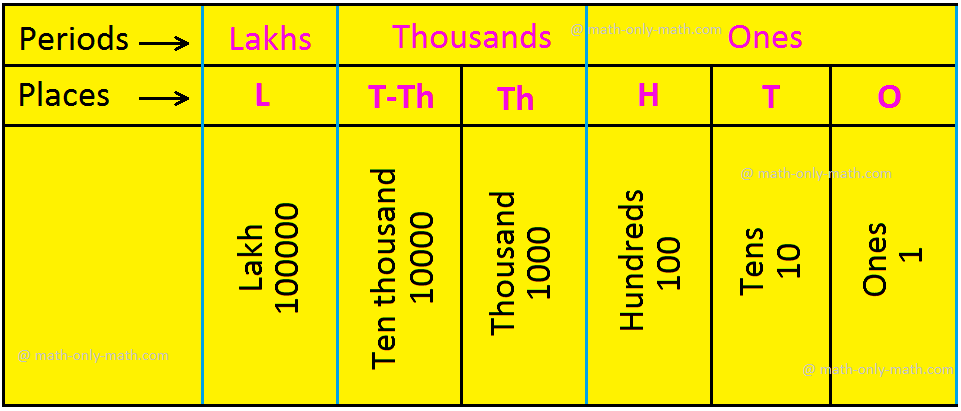
Indian Place-Value Chart
We know that in the Indian place-value chart, we move from right to left. Each place-value represents 10 times the place-value to its immediate right. The following place-value chart shows nine places. Starting from the right the nine places are grouped into four periods namely ones, thousands, lakhs and crores. Each period is separated by a comma.
To read a large number we say, the name for the number followed by the name of the period from left to right. To write a large number from word form to the standard form we substitute digits corresponding to the number for each period from left to right. We use commas in place of periods names.
When a period contains zero, we do not name that period in the word form.
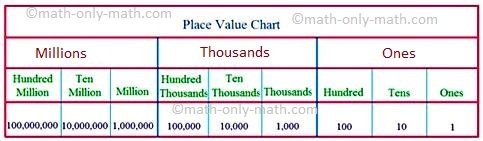
With the increase in the number of digits, the place value chart extends to the left. The place value chart showing the first six places in the numeration system is given below.
Note: The value of a place in the place value chart is 10 times the value of the place next to its right.
|
10 ones 10 tens 10 Hundreds 10 thousand 10 ten thousands |
= 1 ten = 1 hundred = 100 ones = 1 thousand = 100 tens = 1 ten thousand = 1 lakh = 100 thousands |
Index form
|
10 100 1000 10000 100000 |
= 10 × 10 = 10 × 10 × 10 = 10 × 10 × 10 × 10 = 10 × 10 × 10 × 10 × 10 |
= 10\(^{1}\) (ten power 1) = 10\(^{2}\) (ten power 2) = 10\(^{3}\) (ten power 3) = 10\(^{4}\) (ten power 4) = 10\(^{5}\) (ten power 5) |
The power indicates the number of times 10 is multiplied and hence the number of zeroes present in the number.
|
1 lakh 10 lakhs 10 10\(^{0}\) |
= 10\(^{5}\) = 10\(^{5}\) × 10 = 10\(^{6}\) = 1000000 = 10\(^{1}\) = 1 |
Any number raise to the power of zero is 1.
For example,
|
50\(^{0}\) 19\(^{0}\) 100\(^{0}\) |
= 1 = 1 = 1 |
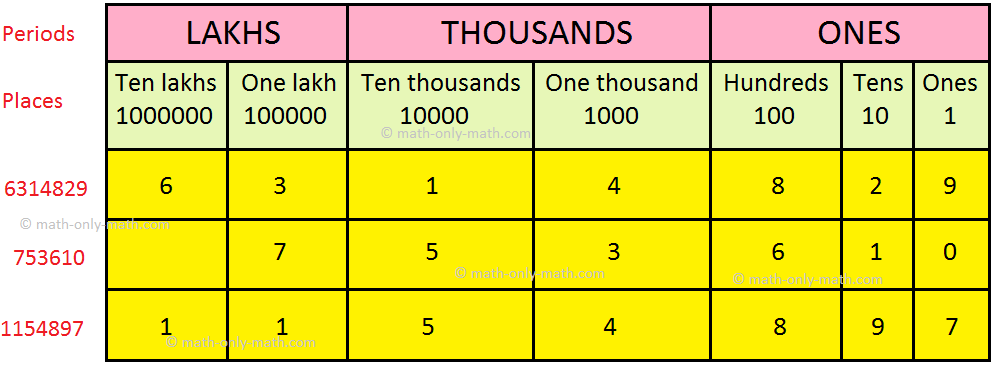
Periods
To read large numbers without difficulty, we group the places into periods in the place value chart as shown below.
The first three places (1st, 2nd and 3rd) from the right make the ‘ones’ period.
The next two place (4th and 5th) make the ‘thousands’ period.
The 6th and 7th places from the right make the ‘lakhs’ period.
We put a comma to separate hundreds from thousands and thousands from lakhs.
While reading the numeral all the digits in the same period are read together and the name of the period (except the ones) is read along with them.
For Examples:
We read 6314829 as sixty three lakhs, fourteen thousands, eight hundred and twenty nine.
7,53,610 → Seven lakhs, fifty three thousands, six hundred and ten.
11,54,897 → Eleven lakhs, fifty four thousands, eight hundred and ninety seven.
The largest 6-digit number is 999999 (nine lakhs ninety nine thousand nine hundred and ninety nine)
9,99,999
+ 1
10,00,000 → The smallest 7-digit number is read as ten lakhs.
The largest 7-digit number is 9999999 (ninety nine lakhs ninety nine thousand nine hundred and ninety nine.
9999999
+ 1
10000000 → The smallest 8-digit number is read as one crore.
Summarization:
To read and write large, numbers we use the following Indian place-value chart :
In the above place-value chart, the six places are grouped into periods.
The first three places from the right end are grouped under 'ones period'.
The next two places are grouped under 'thousands period' and
The last one place is grouped under 'lakhs period'.
To read large numbers, we use the periods.
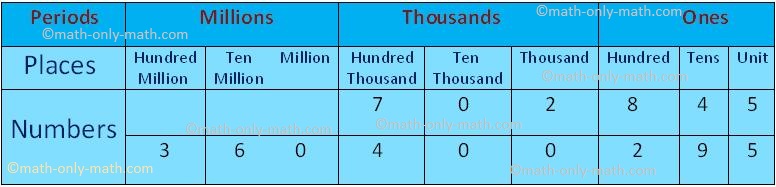
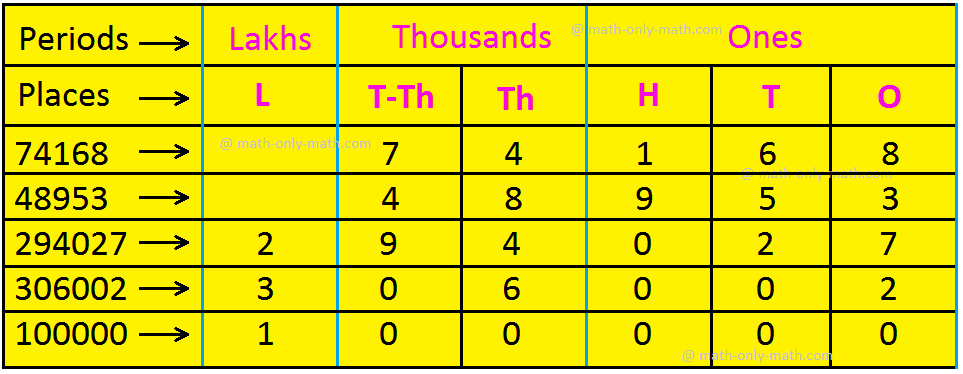
Observe the following place-value chart in which the digits of the numbers: 74168, 48953, 294027, 306002 and 100000 are arranged.
While reading a number, all the digits in the same period are read together and the name of the period (except the ones) is read along with them.
While writing a number, we put a comma after every period to separate the periods. This helps us to read the number easily.
Note: We never write the plural for the periods. It is not 4 lakhs, it is 4 lakh. It is not forty thousands, it is forty thousand.
The extended form of the place value chart is shown below. This system of reading and writing numbers is known as the INDIAN SYSTEM.
The place value chart given above is known as THE INDIAN PLACE VALUE CHART.
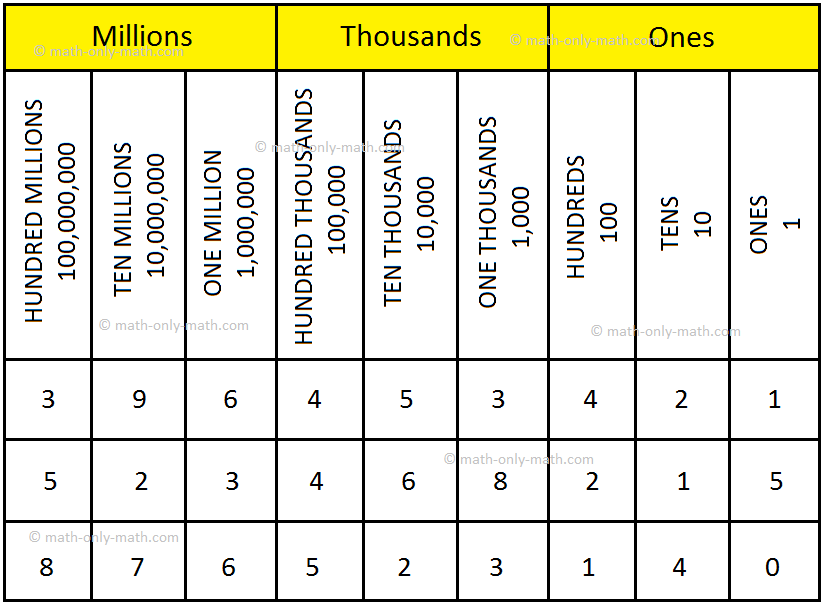
There is yet another form of place value chart which is followed by most of the countries. It is known as THE INTERNATIONAL SYSTEM or BRITISH SYSTEM.
In this system the digits in a number are separated into groups of three called periods.
The first period from the right is called ‘ones’ period, the next period is called ‘thousands’ period and the third period is called the ‘millions’ period. In this system also, all the digits in the same period are read together and the name of the period (except the ones) is read along with them.
The place value chart given below is known as THE INTERNATIONAL PLACE VALUE CHART.
For example:
(i) 396,453,421 read as ‘three hundred and ninety six million, four hundred and fifty three thousand, four hundred and twenty one’.
(ii) 523,468,215 read as ‘five hundred and twenty three million, four hundred and sixty eight thousand, two hundred and fifteen’.
(iii) 876,523,140 read as ‘eight hundred and seventy six million, five hundred and twenty three thousand, one hundred and forty’.
Index Form:
|
1 lakh 10 lakhs 1 crore 10 crores |
= 100 thousand = 1 million = 10 million = 100 million |
= 10\(^{5}\) = 10\(^{6}\) = 10\(^{7}\) = 10\(^{8}\) |
Solved Examples on Indian Place-Value Chart:
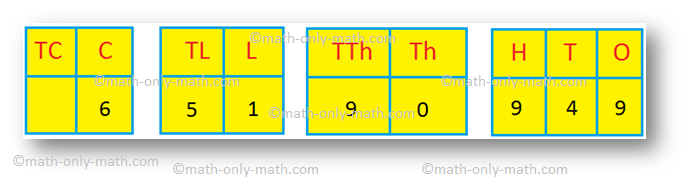
1. Insert commas and express the following numbers in figures.
Seventy-four crore, three lakhs, forty-one thousand six hundred four.
Solution:
Starting from left we enter the digits from crores, lakhs, thousands and ones in the following place-value chart.
Thus, the above number is read as 33,03,41,504
2. Write the number 6,51,90,949 in words.
Solution:
We enter the digits in the places-value chart starting from right to left.
The number is written as six crore, fifty-one lakh, ninety thousand, nine hundred forty-nine.
Note:
A place that has zero in the standard form of a number is not represented in its word form.
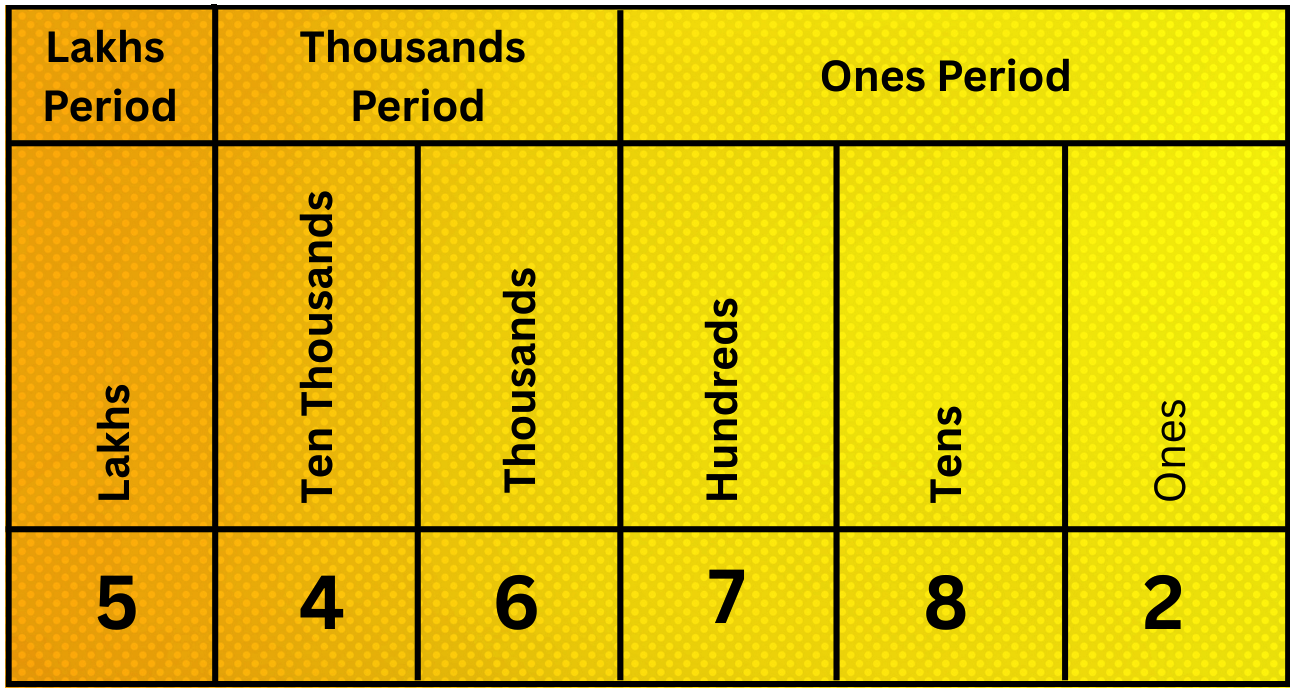
3. Insert commas and express the following numbers in words. Find the place values of each digit. Finally express the digit in expanded form.
546782
Solution:
The given number is 546782.
Let us represent 546782 in place value chart.
To write its number name, consider the following:
It is a 6-digit number, so first place value from the left will be lakhs.
By using commas between the periods in this number, we get 5,46,782.
Hence, the number name will be five lakh forty-six thousand seven hundred eighty-two.
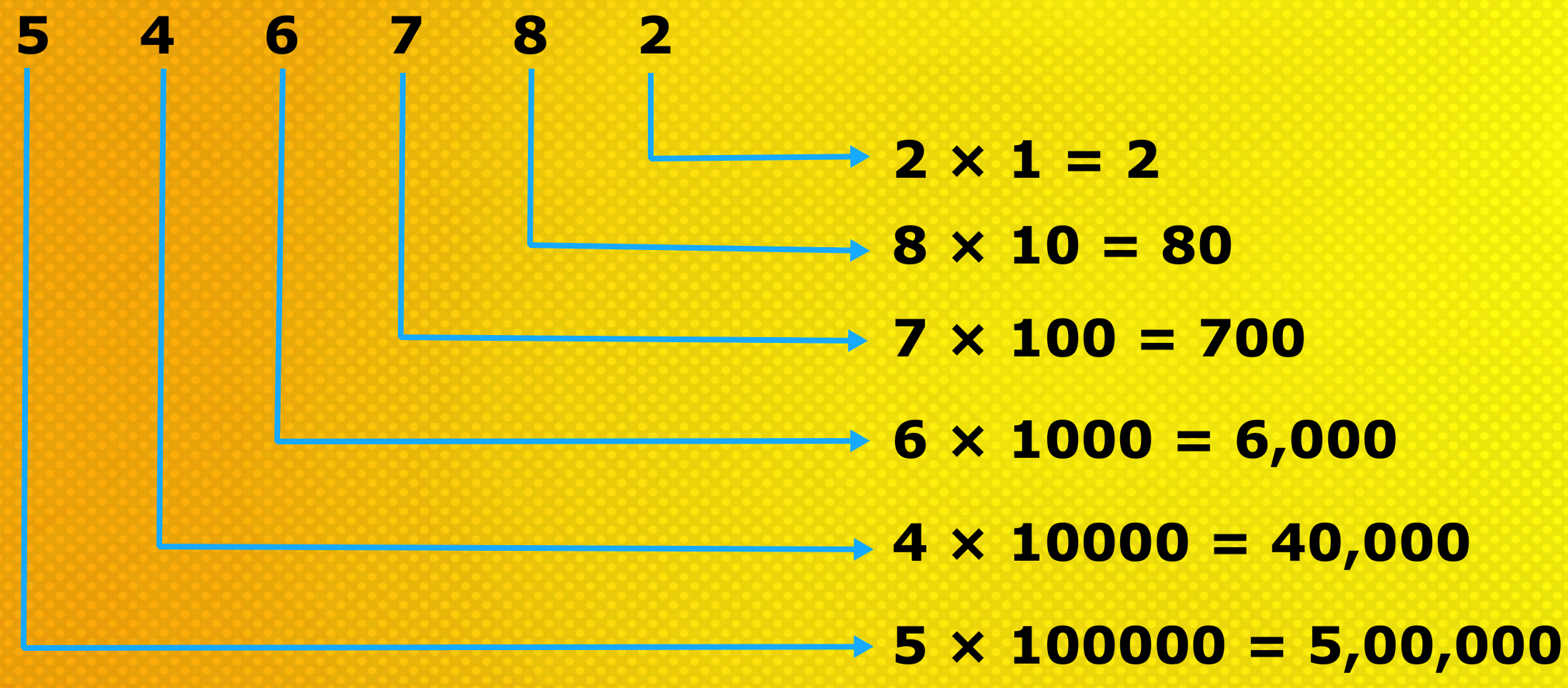
To find the place values of the digits in this number, we have the following:
To write the expanded form, we add the place values, starting from the highest.
5,46,782 = 5,00,000 + 40,000 + 6,000 + 700 + 80 + 2
Worksheet on Place Value Chart:
1. Write the number names for the following numerals.
(i) 24382
(ii) 89431
(iii) 65428
(iv) 56467
(v) 36009
(vi) 11007
(vii) 24725
(viii) 19391
2. Write the numerals for the following number names:
(i) Seventy five thousand five hundred and forty four.
(ii) Eighty two thousand five hundred and thirteen.
(iii) Seventy thousand five hundred and ten
(iv) Eighty nine thousand three hundred and twenty four
(v) Ninety thousand six hundred and twenty five
3. Fill in the blanks:
(i) ............... hundreds = 1 thousand
(ii) 1 ten thousand = ............... thousands
(iii) ............... thousands = 1 lakh
(ii) 100 tens = ............... thousand
4. Write the numerals of:
(i) Seventy nine lakhs, ninety six thousand four hundred and nine.
(ii) Fifteen million, eight hundred and sixty four thousand, two hundred thirty nine.
(iii) Twenty four million, three hundred and fifty seven thousand, one hundred and forty eight.
(iv) Ninety nine lakhs ninety nine thousand nine hundred and ninety nine.
(v) Fifty six million.
5. Write the number-name for each of the following numbers:
(i) 31, 842
(ii) 4, 20, 731
(iii) 8, 52, 249
Answer:
(i) Thirty-one thousand eight hundred forty-two.
(ii) Four lakh twenty thousand seven hundred thirty-one.
(iii) Eight lakh fifty-two thousand two hundred forty-nine.
1. What is Place Value Chart in Maths?
1. What is Place Value Chart in Maths?
Answer: We know the place values from ones to lakhs. To read and write the large numbers more easily, these place values are separated into groups called periods.
The place value chart shows three periods.
The ones period has three places (hundreds, tens, ones)..
The thousands period has two places (ten thousands and thousands).
The lakhs period has two places (lakhs and ten lakhs). Here, one place out of these two places is shown.
To read and write a large number easily, we use commas to separate the periods.
Related Concept
- Formation of Numbers.
- Finding Out the Numbers
- Names of the Numbers.
- Numbers Showing on Spike Abacus.
- 1 Digit Number on Spike Abacus.
- 2 Digits Number on Spike Abacus.
- 3 Digits Number on Spike Abacus.
- 4 Digits Number on Spike Abacus.
- 5 Digits Number on Spike Abacus.
- Large Number.
- Place Value Chart.
- Place Value.
- Problems Related to Place Value.
- Expanded form of a Number.
- Standard Form.
- Comparison of Numbers.
- Example on Comparison of Numbers.
- Successor and Predecessor of a Whole Number.
- Arranging Numbers.
- Formation of Numbers with the Given Digits.
- Formation of Greatest and Smallest Numbers.
- Examples on the Formation of Greatest and the Smallest Number.
- Rounding off Numbers.
4th Grade Math Activities
From Place Value Chart to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.






New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.