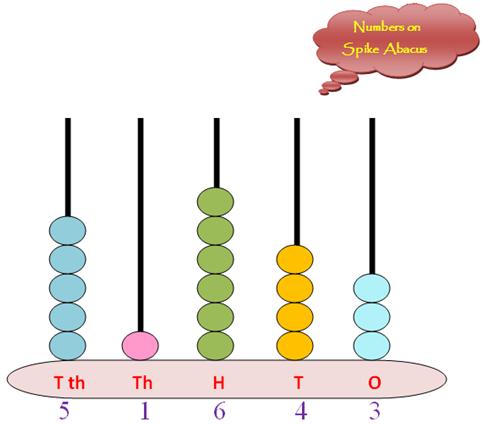
Numbers Showing on Spike Abacus

Numbers showing on spike abacus helps the students to understand the number and its place value. Spike abacus is very helpful to understand the concept of magnitude and name of a number. We know that the spike-abacus represents the number of multi-digits where the digits are represented by the spikes of the abacus.

The spikes from right to left represent the places of the place values of the digits in increasing order i.e., 1, 10, 100, ………. etc.

These places are denoted by O (unit or ones), T (tens), H (hundreds), Th (thousands), T th (ten thousands), H th (hundred thousands) and so on ……… .

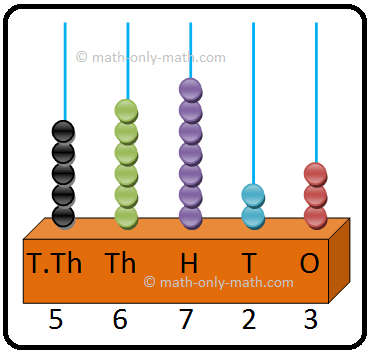
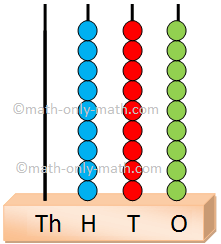
From the above abacus we can count the beads from right to left and then write the exact number i.e., 51643.

O (unit or ones) ----- In ones or unit place we see 3 beads. 

T (tens) ----- In tens place we see 4 beads. 

H (hundreds) ----- In hundreds place we see 6 beads.

Th (thousands) ----- In thousands place we see 1 bead. 

T th (ten thousands) ----- In ten thousands place we see 5 beads. 

Under this topic we will mainly learn about showing the 1 digit number on spike abacus, 2 digits number on spike abacus, 3 digits number on spike abacus, 4 digits number on spike abacus, 5 digits number on spike abacus and so on….

Representation of Numbers on the Abacus:

We can show 1000 on an abacus with four vertical rods. The rods represent place value of thousands, hundreds, tens and ones. We add beads on the rods to show different numbers. Each rod can hold up to 9 beads.

This shows 9 tens and 9 ones. The number is 99.	If we add 1 more to 99 it is 10 tens. Regroup 10 tens as 1 hundred.
This shows 9 hundreds, 9 tens and 9 ones. The number is 999.	If we add 1 more to 999 it is 10 hundreds. Regroup 10 hundreds as 1 thousand. 1 bead in the thousands place represents 1 thousand.

1 bead in the thousands place represents 1 thousand.

Representing 5-Digit and 6-Digit Numbers on the Abacus:

Let us represent the 5-digit and 6-digit numbers on the abacus.

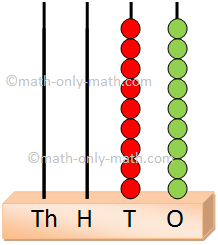
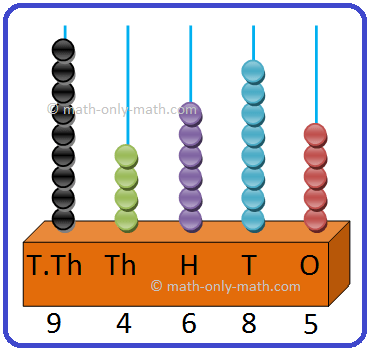
(i) 56723 = Fifty six thousand seven hundred and twenty three.

56723 = 5 × 10000 + 6 × 1000 +              7 × 100 + 2 × 10 + 3 × 1

(ii) 94685 = Ninety four thousand six hundred and eighty five.

94685 = 9 × 10000 + 4 × 1000 +              6 × 100 + 8 × 10 + 5 × 1

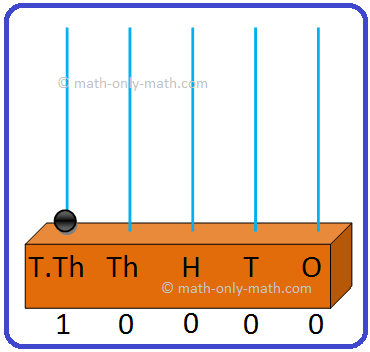
(iii) 100000 = One lakh

100000 = 1 × 100000 + 0 + 0 +                0 + 0 + 0

Related Concept

● Formation of Numbers.

● Finding Out the Numbers

● Names of the Numbers.

● Numbers Showing on Spike Abacus.

● 1 Digit Number on Spike Abacus.

● 2 Digits Number on Spike Abacus.

● 3 Digits Number on Spike Abacus.

● 4 Digits Number on Spike Abacus.

● 5 Digits Number on Spike Abacus.

● Large Number.

● Place Value Chart.

● Place Value.

● Problems Related to Place Value.

● Expanded form of a Number.

● Standard Form.

● Comparison of Numbers.

● Example on Comparison of Numbers.

● Successor and Predecessor of a Whole Number.

● Arranging Numbers.

● Formation of Numbers with the Given Digits.

● Formation of Greatest and Smallest Numbers.

● Examples on the Formation of Greatest and the Smallest Number.

● Rounding off Numbers.

4th Grade Math Activities

From Numbers Showing on Spike Abacus to HOME PAGE