Arranging Numbers

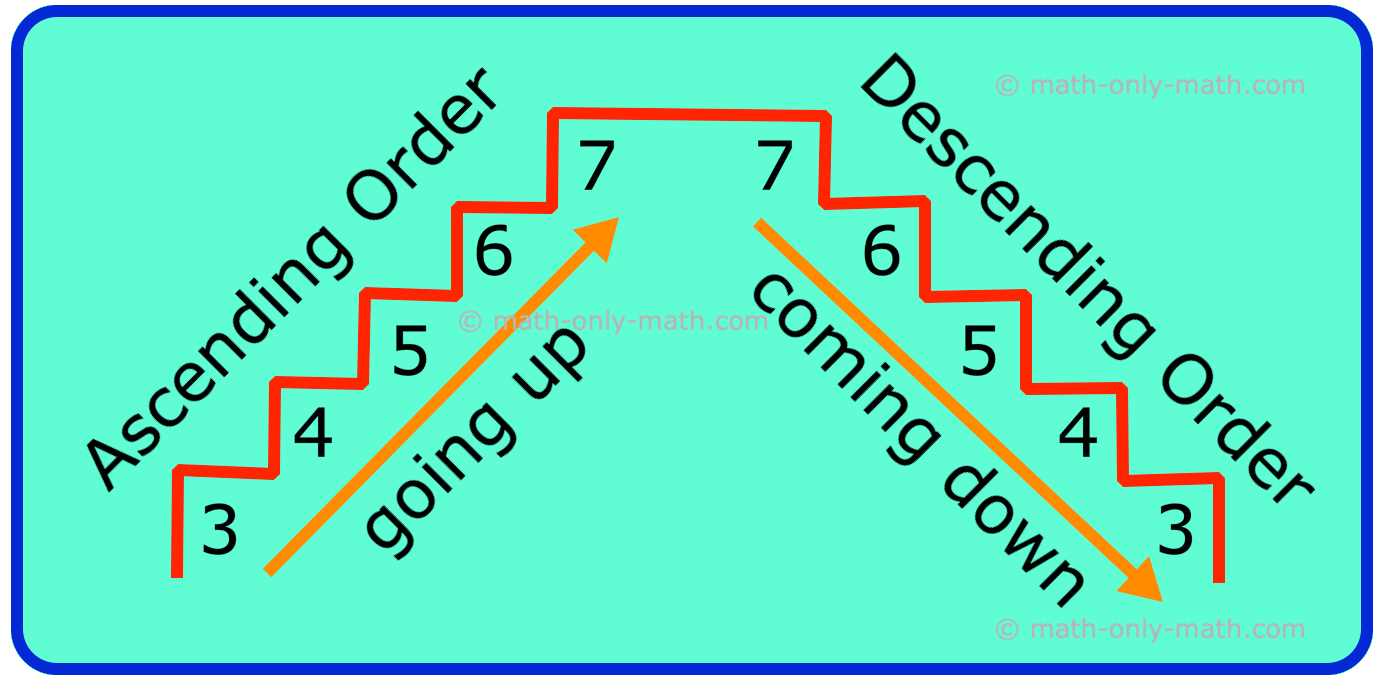
Arranging numbers in ascending order and descending order.

We know, while arranging numbers from the smallest number to the largest number, then the numbers are arranged in ascending order. 

Suppose for example, 81, 97, 123, 137 and 201 are arranged in ascending order. 

Vice-versa while arranging numbers from the largest number to the smallest number then the numbers are arranged in descending order. 

Suppose for example, 187, 121, 117, 103 and 99 are arranged in descending order.

Examples on Arranging numbers in Ascending Order:

Ascending Order: When we write a given set of numbers in order from the smallest to the greatest, they are said to be in ascending order.

1. Write the following numbers is ascending order: 

42734; 5358; 42876; 52287. 

Solution:

Count the digits in each number.

5358 Is the smallest number as it has only 4 digits.

Line up the number accordingly to place value.

Begin comparing from the left.

5358 ← smallest number

42734

42876

7 < 8

52287 ← Largest number

The ascending order is 5358; 42734; 42876; 52287

2. Arranging numbers in ascending order:

3679; 3542; 3797; 3545

Solution:

The digit in the hundreds place in each number is 3.

On comparing the hundreds place; 3679; 3542; 3797; 3545

We find: 3797 to be the greatest and 3679 to be smaller.

On comparing the tens place in the two remaining numbers we find both

numbers to be the same. 3542; 3545

On comparing the ones place, we find 3545 > 3542

So, the ascending order is 3542 < 3545 < 3679 < 3797

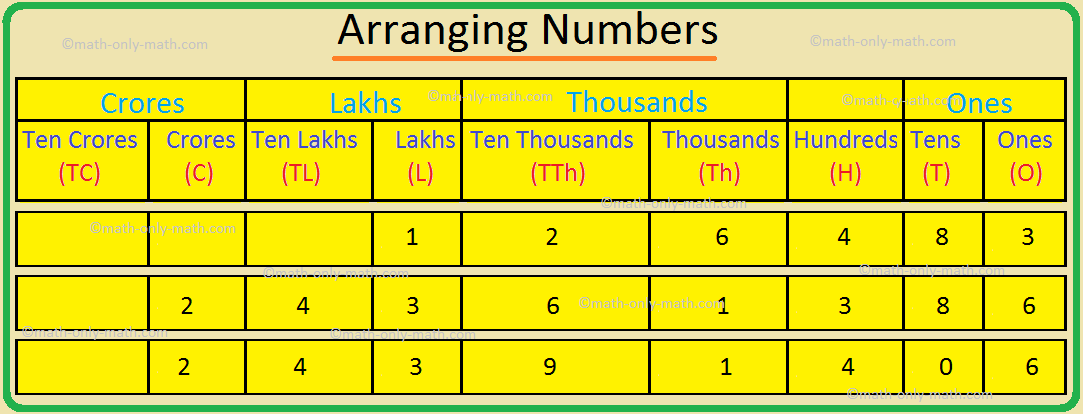
3. Arrange 1,26,483; 2,43,61,386 and 2,43,91,406 in ascending order.

Solution:

Place the number one below the other.

Ordering Numbers

By comparing the number of digits we find that the number 1,26,483 is the smallest number.

Next, comparing 2,43,61,386 and 2,43,91,406 we find that the digits at crores, ten lakhs and lakhs places are same.

Now, compare the digits at ten thousands place. Here, 9 is greater than 6.

So, 2,43,91,406  > 2,43,61,386

Hence, the given numbers in ascending order are 

                        1,26,483; 243,61,386; 2,43,91,406

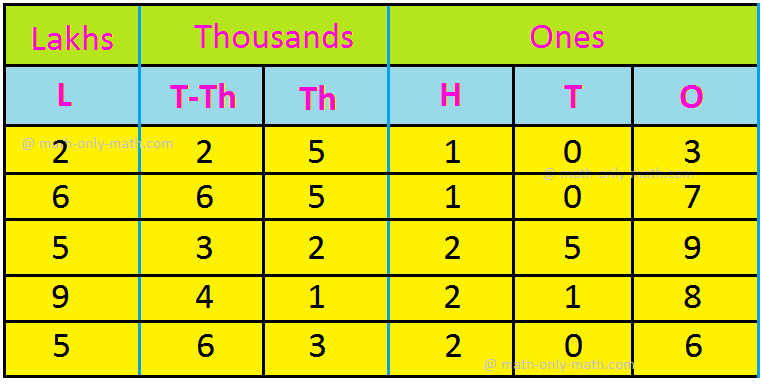
4. Arrange the following numbers in ascending order:

2,25,103;   6,65,107;    5,32,259;    9,41,218;    5,63,206

Solution:

First we arrange the given numbers in a place-value chart:

All the numbers have 6 digits. Comparing the digits at the lakhs place, we get 2 < 5 < 6 < 9.

Now we compare 5,32,259 and 5,63,206. Both these numbers have the same digits at the lakhs place.

So, we compare the digits at the ten-thousands place.

This digit is 3 in 5,32,259 and 6 in 5, 63, 206.

Since 3 < 6             5,32,259 <5,63,206

Thus 2,25,103 < 5,32,259 < 5,63,206 < 6,65,107 < 9,41,218

Hence, the given numbers arranged in ascending order are:

2,25,103; 5,32,259; 5,63,206; 6,65,107; 9,41,218.

5. Considering the numbers 1427, 3246, 3214 and 675, which of the following is a correct ascending order?

(i) 3246 < 3214 < 1427 < 675

(ii) 3214 < 675 < 3246 < 1427

(iii) 675 < 1427 < 3214 < 3246

(iv) 1427 < 675 < 3214 < 3246

Solution:

Step I: No. of digits in 3246 = 4,

            No. of digits in 1427 = 4

            No. of digits in 3214 = 4,

            No. of digits in 675 = 3

            Therefore, 675 is the smallest number.

Step II: Comparing the leftmost digits in 3246, 1427 and 3214, we find that the leftmost digit in each 3246 and 3214 is 3; whereas in 1427 leftmost digit is 1.

Therefore, 1427 is smaller than 3246 and 3214.

Step III: Now, let us compare 3214 and 3246 as shown below.

Therefore, 3214 is less than 3246.

Hence, the given numbers in ascending order are

67514273214 < 3246.

So, the option (iii) is correct, which is the required answer.

Example on Arranging Numbers in Descending order:

1. Write in descending order:

32593; 60537; 28524; 57198

Solution:

Compare digits according to place value. 

Descending order means arranging numbers from the largest number to the smallest number; 

60537 > 57198 > 32593 > 28524

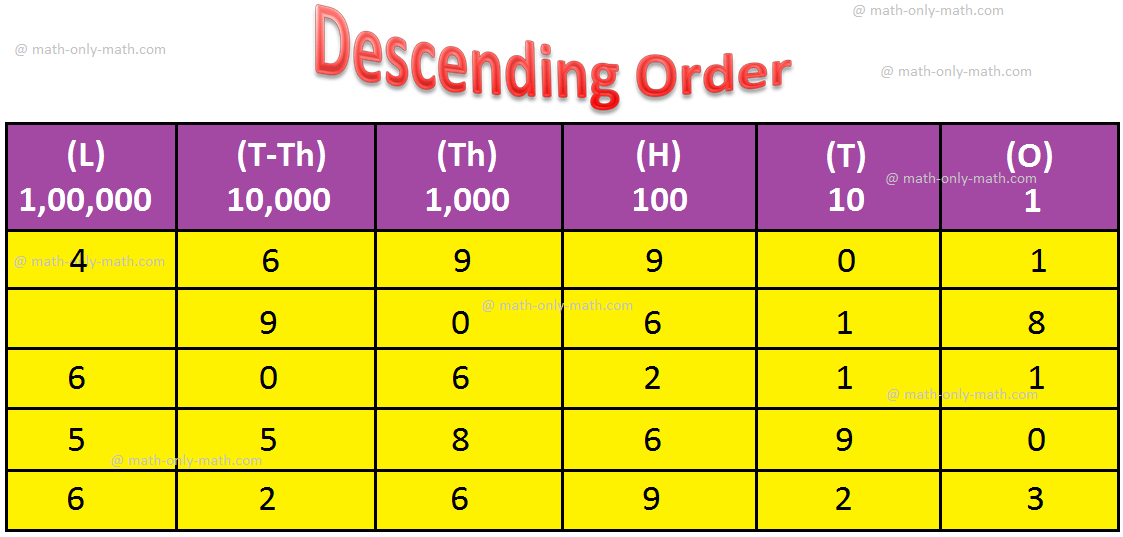
2. Arrange the following numbers in descending order:

4,69,901;    90,618;    6,06,211;    5,58,690;   6,26,923

Solution: First we arrange the given numbers in a place-value chart:

90, 618 is a 5-digit number. All others are 6-digit numbers.

So, 90,618 is the smallest number.

Comparing the digits at the lakhs place we get 6 > 5 > 4.

Now, we compare 6,06,211 and 6,26,923. Both the numbers have 6 at lakhs place.

So, we compare their digits at the ten-thousands place.

This digit is 0 in 6,06,211 and 2 in 6,26,923.

So, 6,06,211 < 6,26,923.

Thus, 6,26,923 > 6,06,211 > 5,58,690 > 4,69,901 > 90,618.

Hence, the given numbers arranged in descending order are:

6,26,923;   6,06,211;   5,58,690;   4,69,901;   90,618.

Word Problems on Arranging Numbers:

1. The monthly salary of 4 friends are $2,455, $6945, $4300 and $8000. Arrange the salaries in ascending order.

Solution: 

Among the following 2455 is smallest and 8000 is greatest.

Therefore, the given salaries in ascending order are $ 2455 < $4300 < $6945 < $8000.

Worksheet on Ascending and Descending Order:

1. Rewrite the following numbers in the ascending order and descending order.

(i) 94257, 94527, 94752, 94725

(ii) 359421, 354921, 359412, 354912

(iii) 50050, 50500, 55000, 50005

Answer:

1. (i) Ascending Order   : 94257; 94527; 94725; 94752

        Descending Order : 94752; 94725; 94527; 94257

(ii)    Ascending Order   : 354912; 354921; 359412; 359421

        Descending Order : 359421; 359412; 354921; 354912

(iii)   Ascending Order   : 50005; 50050; 50500; 55000

        Descending Order : 55000; 50500; 50050; 50005

2. Arrange the following in descending order:

(i) 1149; 2348; 126; 95

(ii) 262; 1313; 12; 28

(iii) 114; 4963; 234; 345

(ιν) 7628; 88; 329; 18

(v) 315; 735; 1957; 49

(vi) 9; 3496; 777; 920

Answer:

2. (i) 2348; 1149; 126; 95

(ii) 1313; 262; 28; 12

(iii) 4963; 345; 234; 114

(ιν) 7628; 329; 88; 18

(v) 1957; 735; 315; 49

(vi) 3496; 920; 777; 9

3. Arrange the following in ascending order:

(i) 223; 8962; 1259; 135

(ii) 962; 819; 23; 67

(iii) 23; 5964; 95; 398

(iv) 2319; 2391; 3219; 3291

(ν) 1083; 1038; 1033; 10881

Answer:

3. (i) 135; 223; 1259; 8962

(ii) 23; 67; 819; 962;

(iii) 23; 95; 398; 5964

(iv) 2319; 2391; 3219; 3291

(ν) 1033; 1038; 1083; 10881

4. Multiple Choice Questions (MCQs) on Comparison of Numbers:

    Select the right option.

(i) Which one of the following is a correct descending order?

(a) 4962 > 349 > 4968 > 423

(b) 4962 > 423> 4968 > 349

(c) 4968 > 423 > 4962 > 349

(d) 4968 > 4962 > 423 > 349.

Answer:

4. (i) (d) 4968 > 4962 > 423 > 349.

5. State True or False.

Ascending order of 3459, 1732, 6895, 247 is

247 < 1732 < 3459 < 6895

Answer: True

Frequently Asked Questions on Arranging Numbers:

Related Concept 

• Formation of Numbers.
• Finding Out the Numbers
• Names of the Numbers.
  
• Numbers Showing on Spike Abacus.
  
• 1 Digit Number on Spike Abacus.
  
• 2 Digits Number on Spike Abacus.
  
• 3 Digits Number on Spike Abacus.
  
• 4 Digits Number on Spike Abacus.
  
• 5 Digits Number on Spike Abacus.
  
• Large Number.
• Place Value Chart.
• Place Value.
• Problems Related to Place Value.
• Expanded form of a Number.
• Standard Form.
• Comparison of Numbers.
• Example on Comparison of Numbers.
• Successor and Predecessor of a Whole Number.
  
• Arranging Numbers.
  
• Formation of Numbers with the Given Digits.
• Formation of Greatest and Smallest Numbers.
• Examples on the Formation of Greatest and the Smallest Number.
• Rounding off Numbers.

4th Grade Math Activities

From Arranging Numbers to HOME PAGE