Successor and Predecessor

The successor and predecessor of a whole number are discussed below:

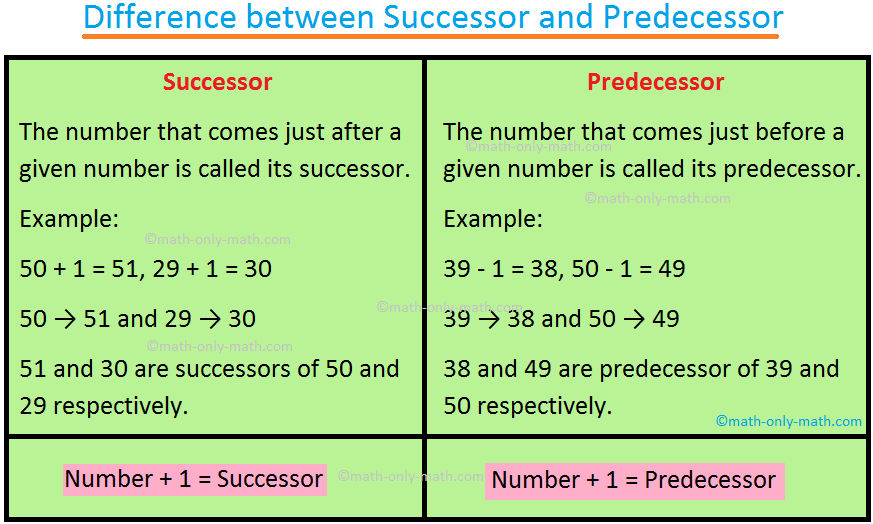
The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number.

For example, 9,99,99,999 is predecessor of 10,00,00,000 or we can also say 10,00,00,000 is the successor of 9,99,99,999.

Definition of Successor:

The number which comes immediately after a particular number is called its successor.

How to find the successor of a number?

The successor of a whole number is the number obtained by adding 1 to it.

Clearly, the successor of 0 is 1; successor of 1 is 2; successor of 2 is 3 and so on.

$Successor and Predecessor$

We observe that every whole number has its successor.

Number + 1 = Successor

Definition of Predecessor:

The number which comes just before a particular number is called its predecessor.

The predecessor of a whole number is one less than the given number.

How to find the predecessor of a number?

Clearly, the predecessor of 1 is 0; predecessor of 2 is 1; predecessor of 3 is 2 and so on.

The whole number 0 does not have any predecessor.

We observe that every whole number, other than zero, has its predecessor.

Also, if a is the successor of b, then b is the predecessor of a.

Number + 1 = Predecessor

Solved Examples on Successor and Predecessor of a Number:

Find the successor and predecessor of each of the following whole numbers:

(i) 1000

(ii) 11999

(iii) 400099

(iv) 1000001

(v) 99999

Solution:

(i) 1000

The successor of 1000 is (1000 + 1) = 1001.

The predecessor of 1000 is (1000 - 1) = 999.

(ii) 11999

The successor of 11999 is (11999 + 1) = 12000.

The predecessor of 11999 is (11999 - 1) = 11998.

(iii) 400099

The successor of 400099 is (400099 + 1) = 400100.

The predecessor of 400099 is (400099 - 1) = 400098.

(iv) 1000001

The successor of 1000001 is (1000001 + 1) = 1000002.

The predecessor of 1000001 is (1000001 - 1) = 1000000.

(v) 99999

The successor of 99999 is (99999 + 1) = 100000.

The predecessor of 99999 is (99999 - 1) = 99998.

$Successor and Predecessor of a Whole Number$

What is Successor and Predecessor of a number?

The Successor and Predecessor of a number are explained using examples.

PREDECESSOR NUMBER SUCCESSOR

(7148 - 1) 7147 7148 (7148 + 1) 7149

(8950 - 1) 8949 8950 (8950 + 1) 8951

(7620 - 1) 7619 7620 (7620 + 1) 7621

(12499 - 1) 12498 12499 (12499 + 1) 12500

To find the predecessor of a number, subtract 1 from the given number.

To find the successor of a number add 1 to the given number.

Difference between Successor and Predecessor:

$Difference between Successor and Predecessor$

1. Write the successor of the given numbers.

(i) 78,95,226

(ii) 10,00,999

(iii) 49,99,999

(iv) 48,09,826

(v) 8,00,78,593

Solution:

(i) The successor of 78,95,226 is (78,95,226 + 1) = 78,95,227

(ii) The successor of 10,00,999 is (10,00,999 + 1) = 10,01,000

(iii) The successor of 49,99,999 is (49,99,999 + 1) = 50,00,000

(iv) The successor of 48,09,826 is (48,09,826 + 1) = 48,09,827

(v) The successor of 8,00,78,593 is (8,00,78,593 + 1) = 8,00,78,594

2. Write the predecessor of the given numbers.

(i) 47,89,300

(ii) 89,78,515

(iii) 78,45,000

(iv) 99,30,799

(v) 85,83,221

Solution:

(i) The predecessor of 47,89,300 is (47,89,300 - 1) = 47,89,299

(ii) The predecessor of 89,78,515 is (89,78,515 - 1) = 89,78,514

(iii) The predecessor of 78,45,000 is (78,45,000 - 1) = 7844999

(iv) The predecessor of 99,30,799 is (99,30,799 - 1) = 99,30,798

(v) The predecessor of 85,83,221 is (85,83,221 - 1) = 85,83,220

Questions and Answers on Successor and Predecessor of a Number:

I. Write predecessor and successor of the given number

(i)

Number	Successor
321	322
4567	__________
9876	__________

(ii)

Number	Predecessor
768	767
2010	__________
5642	__________

Answers:

I. (i) 4568, 9877

(ii) 2009, 5641

II. Write the successor of each of the following numbers:

(i) 5673

(ii) 2190

(iii) 2045

(iv) 1044

(v) 3109

(vi) 4005

(vii) 8711

(viii) 1241

(ix) 3019

(x) 7045

(xi) 4565

(xii) 8454

Answer:

II. (i) 5674

(ii) 2191

(iii) 2046

(iv) 1045

(v) 3110

(vi) 4006

(vii) 8712

(viii) 1242

(ix) 3020

(x) 7046

(xi) 4566

(xii) 8455

III. Write the successor of each of the following numbers:

(i) 5200

(ii) 4715

(iii) 8213

(iv) 5249

(v) 2801

(vi) 9236

(vii) 5612

(viii) 2076

(ix) 5912

(x) 8102

(xi) 7564

(xii) 6458

Answer:

III. (i) 5199

(ii) 4714

(iii) 8212

(iv) 5248

(v) 2800

(vi) 9235

(vii) 5611

(viii) 2075

(ix) 5911

(x) 8101

(xi) 7563

(xii) 6457

● A number that comes just before is called Predecessor.

For example, 55 comes just before 56.

● A number that comes just after any number is called Successor.

For example, 87 comes just after 86.

IV. Write the successors (the number after):

(i) 169 ............

(ii) 372 ............

(iii) 475 ............

(iv) 958 ............

(v) 568 ............

(vi) 872 ............

(vii) 928 ............

(viii) 672 ............

Answer:

IV. (i) 170

(ii) 373

(iii) 476

(iv) 959

(v) 569

(vi) 873

(vii) 929

(viii) 673

V. Write the predecessors (the number before):

(i) ............ 357

(ii) ............ 448

(iii) ............ 785

(iv) ............ 997

(v) ............ 854

(vi) ............ 362

(vii) ............ 999

(viii) ............ 575

Answer:

V. (i) 356

(ii) 447

(iii) 784

(iv) 996

(v) 853

(vi) 361

(vii) 998

(viii) 574

VI. Write the numbers between:

(i) 476 ............ 478

(ii) 758 ............ 760

(iii) 922 ............ 924

(iv) 850 ............ 852

(v) 567 ............ 569

(vi) 397 ............ 399

(vii) 624 ............ 626

(viii) 328 ............ 330

(ix) 246 ............ 248

Answer:

VI. (i) 477

(ii) 759

(iii) 923

(iv) 851

(v) 568

(vi) 398

(vii) 625

(viii) 329

(ix) 247

VII. Complete the patterns:

(i) 672, 676, 680, ............, ............, ............, ............

(ii) 840, 860, 880, ............, ............, ............, ............

(iii) 550, 500, 450, ............, ............, ............, ............

(iv) 965, 970, 975, ............, ............, ............, ............

(v) 430, 460, 490, ............, ............, ............, ............

Answer:

VII. Complete the patterns:

(i) 684, 688, 692, 696

(ii) 900, 920, 940, 960

(iii) 400, 350, 300, 250

(iv) 980, 985, 990, 995

(v) 520, 550, 580, 610

You might like these

$The various types of fractions are: 1. Like fractions: The fractions having the same denominators are known as like fractions.$

Types of Fractions |Like Fractions|Unit fractions|Proper & Improper Fr
The various types of fractions are: 1. Like fractions: The fractions having the same denominators are known as like fractions.
4th Grade Numbers Worksheets | Place Value Chart | Expended Form
In 5th Grade Numbers Worksheets we will solve how to read and write large numbers, use of place value chart to write a number in expanded form, represent the large number on the abacus, write the number in standard form, compare with another number and arrange numbers
Word Problems on Division | Examples on Word Problems on Division
Word problems on division for fourth grade students are solved here step by step. Consider the following examples on word problems involving division: 1. $5,876 are distributed equally among 26 men. How much money will each person get?
Word Problems on Multiplication |Multiplication Word Problem Worksheet
Word problems on multiplication for fourth grade students are solved here step by step. Problem Sums Involving Multiplication: 1. 24 folders each has 56 sheets of paper inside them. How many sheets of paper are there altogether? Solution: We can add 56 sheets 24 times
Division by Two-Digit Numbers | Knowledge of Estimation | Division
In division by two-digit numbers we will practice dividing two, three, four and five digits by two-digit numbers. Consider the following examples on division by two-digit numbers: Let us use our knowledge of estimation to find the actual quotient. 1. Divide 94 by 12
Multiplication of a Number by a 3-Digit Number |3-Digit Multiplication
In multiplication of a number by a 3-digit number are explained here step by step. Consider the following examples on multiplication of a number by a 3-digit number: 1. Find the product of 36 × 137
Division by 10 and 100 and 1000 |Division Process|Facts about Division
Division by 10 and 100 and 1000 are explained here step by step. when we divide a number by 10, the digit at ones place of the given number becomes the remainder and the digits at the remaining places of the number given the quotient.
Terms Used in Division | Dividend | Divisor | Quotient | Remainder
The terms used in division are dividend, divisor, quotient and remainder. Division is repeated subtraction. For example: 24 ÷ 6 How many times would you subtract 6 from 24 to reach 0?
Multiplication | How to Multiply a One, Two or Three-digit Number?
In multiplication we know how to multiply a one, two or three-digit number by another 1 or 2-digit number. We also know how to multiply a four-digit number by a 2-digit number. We also know the different methods of multiplication. Here, we shall make use of the methods and
Subtraction with Regrouping | 4-Digit, 5-Digit and 6-Digit Subtraction
We will learn subtraction 4-digit, 5-digit and 6-digit numbers with regrouping. Subtraction of 4-digit numbers can be done in the same way as we do subtraction of smaller numbers. We first arrange the numbers one below the other in place value columns and then we start
Addition & Subtraction Together |Combination of addition & subtraction
We will solve the different types of problems involving addition and subtraction together. To show the problem involving both addition and subtraction, we first group all the numbers with ‘+’ and ‘-‘ signs. We find the sum of the numbers with ‘+’ sign and similarly the sum
4th Grade Subtraction Worksheets | 4-Digit Subtraction |Math Only Math
In 4th grade subtraction worksheet we will solve 4-Digit Subtraction, word problem on subtraction, Estimate the difference by rounding off the given numbers, successor and predecessor of a number.
Find the Missing Digits | Missing Digits in Addition and Subtraction
How to find the missing digits in the blank spaces? Add the ONES: 5 + 9 = 14 Regroup as 1 Ten and 4 Ones Add the TENS: 2 + 1 carry over = 3 Write 2 in the box to make 3 + 2 = 5 Add the HUNDREDS: 4
Subtraction without Regrouping |4-Digit, 5-Digit & 6-Digit Subtraction
We will learn subtracting 4-digit, 5-digit and 6-digit numbers without regrouping. We first arrange the numbers one below the other in place value columns and then subtract the digits under each column as shown in the following examples. 1. Subtract 3248 from 6589.
Subtraction | How to Subtract 2-digit, 3-digit, 4-digit Numbers?|Steps
The answer of a subtraction sum is called DIFFERENCE. How to subtract 2-digit numbers? Steps are shown to subtract 2-digit numbers.
Addition | Method of Addition | Addition for 4-Digit Numbers | Add
Addition is finding the total of different values. The important thing to remember when adding is to line up the numbers carefully according to place value.
Method of L.C.M. | Finding L.C.M. | Smallest Common Multiple | Common
We will discuss here about the method of l.c.m. (least common multiple). Let us consider the numbers 8, 12 and 16. Multiples of 8 are → 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, ......
Methods of Prime Factorization | Division Method | Factor Tree Method
In prime factorization, we factorise the numbers into prime numbers, called prime factors. There are two methods of prime factorization: 1. Division Method 2. Factor Tree Method
Factors | Understand the Factors of the Product | Concept of Factors
Factors of a number are discussed here so that students can understand the factors of the product. What are factors? (i) If a dividend, when divided by a divisor, is divided completely
Formation of Numbers | Smallest and Greatest Number| Number Formation
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,