Volume of a Cube

A cube is a solid box whose every surface is a square of same area.

Take an empty box with open top in the shape of a cube whose each edge is 2 cm. Now fit cubes of edges 1 cm in it. From the figure it is clear that 8 such cubes will fit in it. So the volume of the box will be equal to the volume of 8 unit cubes together.

Therefore, the volume of the cube = 8 cu cm

Note that 8 = 2 × 2 × 2

Thus, volume of a cube = side × side × side = side³

Hence, a cube has:

(i) six surfaces or faces,

(ii) 8 vertices,

(iii) 12 edges or sides of equal length.

Since a cube has all sides equal.

Volume of a cube = (side × side × side) cubic units.

= 1 × 1 × 1 cubic units

Since area = side × side

Volume of a cube = (area × side) cubic units.

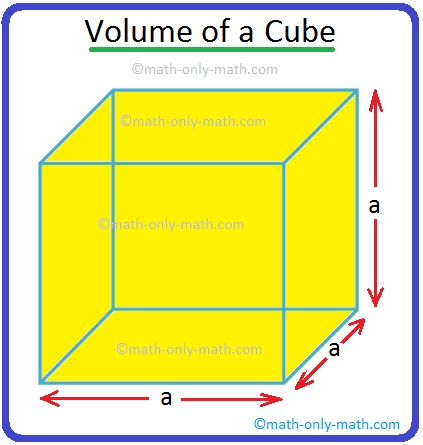
A solid having the same length, breadth and height is called a cube. Length of the cube = breadth of the cube = height of the cube = a cm

Volume of cube = length × breadth × height

                       = a cm × a cm ×  a cm

                       = a³ cm³

So, volume of a cube is (side)³ cm³

Let us consider an example:

1. Find the volume of a cube having each side 6 cm.

Solution:

Side of the cube = 6 cm

Volume of the cube = (side)³

                             = (6 cm)³

                             = (6 × 6 × 6) cm³

                             = 216 cm³

Solved Examples on Volume of a Cube:

1. Find the volume of cuboid by counting the number of cubes.

Solution:

Solution: 

The number of unit cubes are 6, its volume is 6 cu cm.

2. Find the volume of cuboid by counting the number of cubes.

Solution:

Solution:

The number of cubes are 12, its volume is 12 cu cm.

3. Find the volume of a cube whose edge is 5 cm long.

Solution: 

The length of an edge = 5 cm

Volume of a cube = side of edge × side of edge × side of edge

Volume of a cube = 5 cm × 5 cm × 5 cm

                          = 125 cu cm

                          = 125 cm³

4. Find the volume of a cube of side 7 cm.

Solution: 

We know, volume of a cube = (side × side × side) cubic units.

Here, side = 7 cm.

               = 7 × 7 × 7

               = 343

Therefore, volume of a cube = 343 cubic cm.

5. Find the volume of a cube of side 13 cm.

Solution: 

We know, volume of a cube = (side × side × side) cubic units.

Here, side = 13 cm.

                = 13 × 13 × 13

                = 2197

Therefore, volume of a cube = 2197 cubic cm.

6. Find the volume of water that can be contained in a cubical container each of whose edge measure 2 m internally.

Solution: 

The internal length of an edge of the container = 2 m

The internal volume of the container = 2 m × 2 m × 2 m = 8 cu m

The volume of water that the container can hold = the internal volume of the container.

Therefore, the required volume of water = 8 cu m.

Worksheet on Volume of a Cube

Questions and Answers on Cube:

1. Find the volume of cubes with each edge measuring:

(i) 5 cm

(ii) 10 m

(iii) 1.1 cm

(iv) 30 mm

(v) 4.3 m

Answers:

(i) 125 cu. cm

(ii) 1000 cu. m

(iii) 1.331 cu. cm

(iv) 2700 cu. mm

(v) 79.507 cu. m

2. Find the volume of cubes having the following sides.

(i) 7 cm

(ii) 11 cm

(iii) 4.5 cm

(iv) 9 cm

(v) 5 cm

(vi) 14 cm

(vii) 12 m

(viii) 8 m

(ix) 6.5 cm

(x) 3 m

(xi) 12 cm

(xii) 6 m

Answer:

2. (i) 343 cm³

(ii) 1331cm³

(iii) 91.125 cm³

(iv) 729 cm³

(v) 125 cm³

(vi) 2744 cm³

(vii) 1728 m³

(viii) 512 m³

(ix) 274.625 cm³

(x) 27m³

(xi) 1728 cm³

(xii) 216 m³

● Volume.

Units of Volume

Cube.

Cuboid.

Practice Test on Volume.

Worksheet on Volume.

5th Grade Geometry

5th Grade Math Problems

From Volume of a Cube to HOME PAGE