Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Construction of a Circle
A circle is a collection of all those point in a plane whose distance from a fixed point remains constant.
Centre: The fixed point in the plane which is equidistant from every point on the boundary of a circle is called centre.
In figure, O is the centre of the circle.
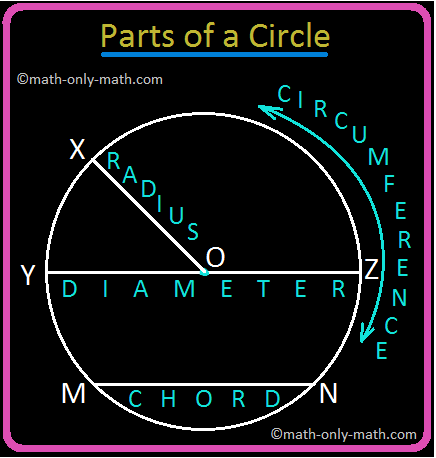
Radius: The fixed distance between the centre and any point on the boundary of the circle is called radius.
In figure, OX is a radius.
Chord: A line segment joining any two points on a circle is called a chord of the circle.
In figure, MN is a chord.
Diameter: A chord that passes through the centre of a circle is called diameter of the circle.
In figure, YZ is a diameter. The length of a diameter = 2 × radius.
In a circle, diameter is the longest chord.
Construction of a Circle when the Length of its Radius is Given:
Working Rules for Construction of a Circle:
Step I: Open the compass such that its pointer be put on initial point (i.e. O) of ruler / scale and the pencil-end be put on a mark say 3 cm (Let the radius of the circle be 3 cm).
Step II: Mark a point with pencil where we want the centre of the circle: Let it be O.
Step III: Place the pointer of the compass on O which we have marked in step II.
Step IV: Turn the compass around the point O to get the required circle.
Constructing a Circle:
We draw a circle with the help of a pair of compasses, provided in the geometry box and a fine pointed pencil.
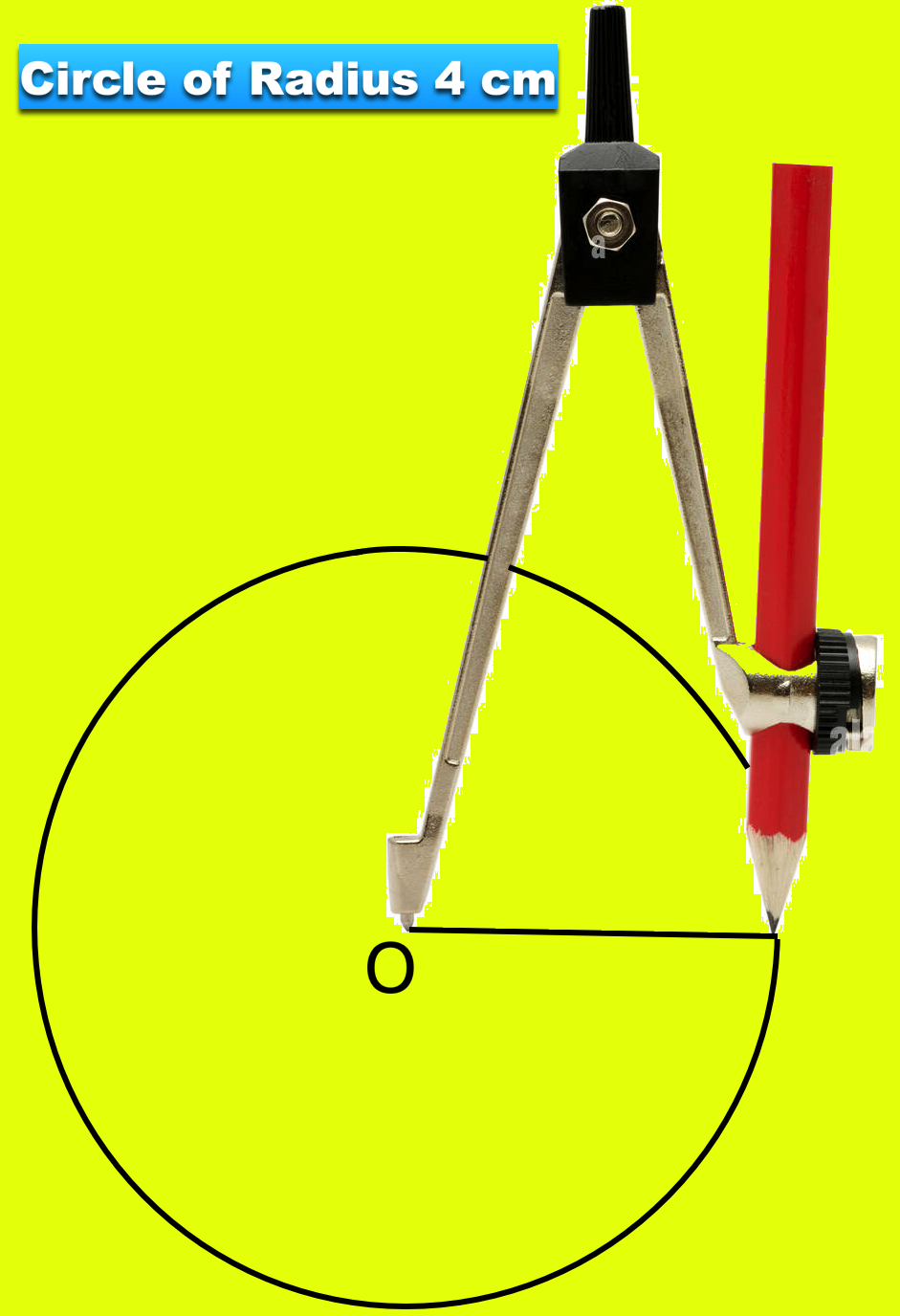
Let us draw a circle of radius 4 cm. We observe the following steps.
Step I: We expand the two arms of a pair of compasses and take the measure of 4 cm on the scale by placing pointed end at zero and the other end having a pencil at 4 cm, mark on the scale as shown in the figure.
Step II: We take a convenient point O on a piece of paper.
Step III: We fix the pointed end of the pair of compasses at O and move the pencil point around holding the pair of compasses firmly at the top. We get the desired round shape called a circle.
Example on Construction of a Circle:
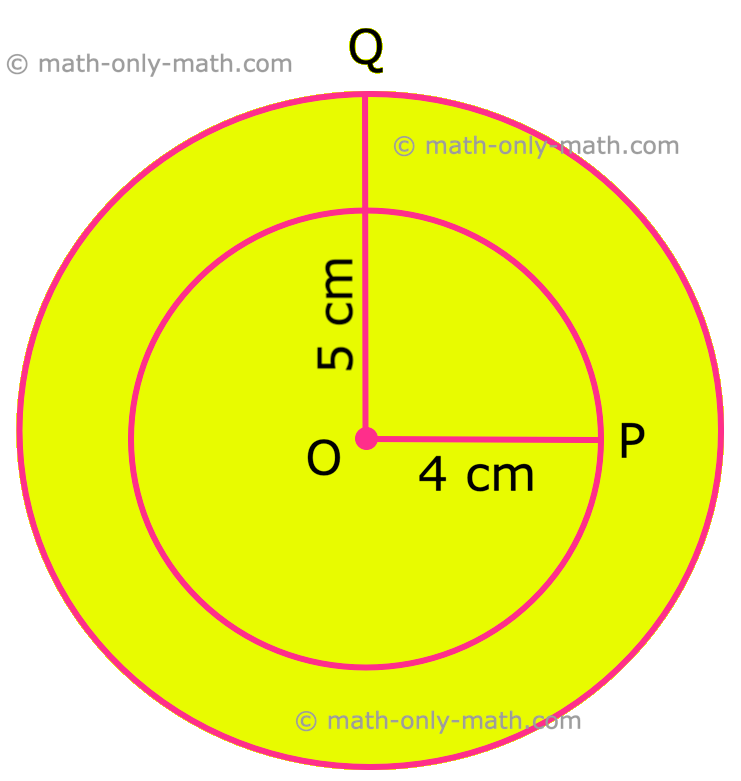
1. Draw two circle of radii 4 cm and 5 cm with same centre O.
I. Open the compass by putting the pointer on initial point of a scale and by opening the pencil-end upto 5 cm.
II. Marka point O with pencil and consider it as centre of the circle.
III. Place the pointer of the compass on O.
IV. Turn the compass around O to get the circle of radius 5 cm.
V. With the help of same above steps, draw an another circle of radius 4 cm having the same O as centre.
Solved Example on Circle:
1. Find the radius of circle whose diameter is 28 cm.
Solution:
Radius of a circle = \(\frac{\textrm{Diameter of the circle}}{\textrm{2}}\)
= \(\frac{28}{2}\) cm
= 14 cm
Worksheet on Construction of a Circle:
1. Multiple Choice Questions (MCQ) on Circle:
Tick (✔) the correct option.
(i) The radius of a circle of diameter 20 cm is
(a) 8 cm
(b) 10 cm
(c) 4.0 cm
(d) 4.5 cm
(ii) Find the diameter of the circle when radius is
(a) 3.8 cm
(b) 7.3 cm
(c) 2.9 cm
(d) 4.8 cm
(iii) O is the centre of a circle, and its radius is 5 cm. Where does P lie, when
(i) OP = 5.2 cm?
(ii) OP = 5cm?
(iii) OP = 4.8 cm?
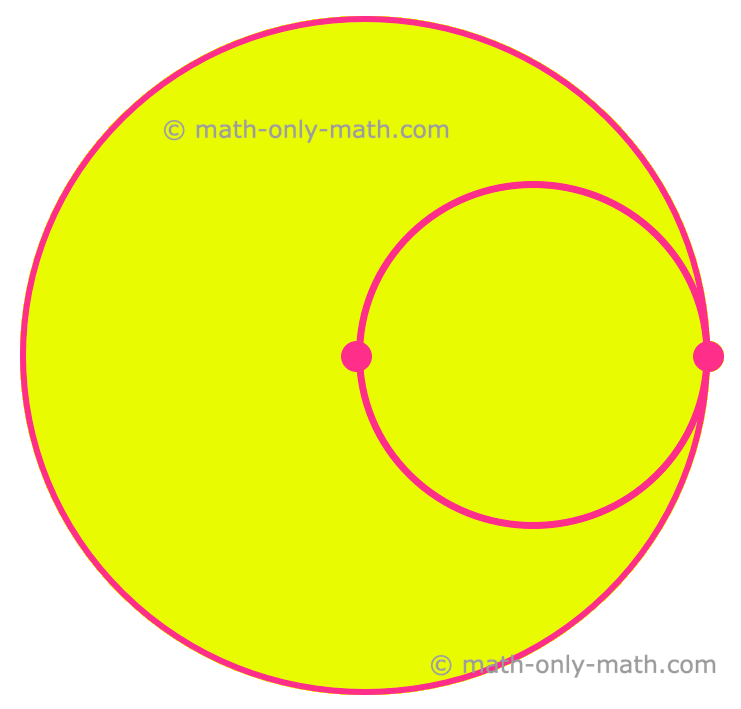
4. Draw two circles one having radius 6 cm and other having 3 cm as shown in the following figure such that the inner circle passes through centre of the other circle.
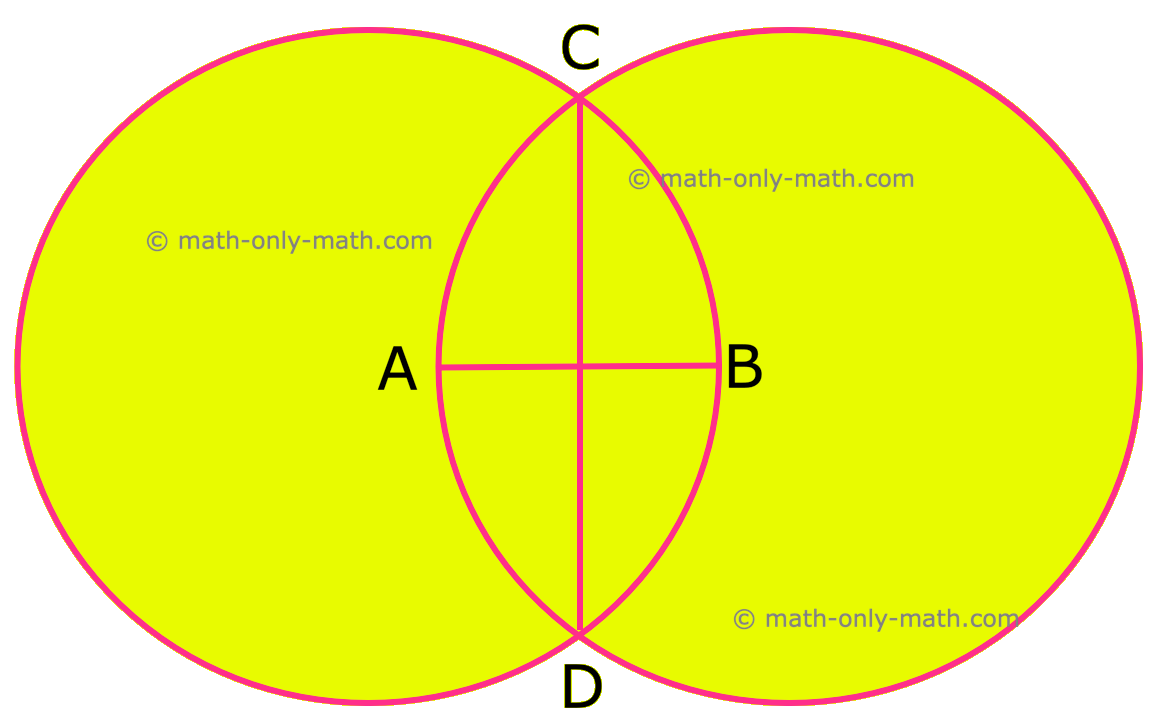
5. Draw two circles of equal radii with centres A and B such that each one of them passes through the centre of the other. Check whether AB ⊥ CD.
6. With the same centre O, draw three circles of radii 2.5 cm, 3.5 cm and 4.5 cm.
From Construction of a Circle to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
