Quadrilateral Worksheet

In math practice test on quadrilateral worksheet we will practice different types of questions in quadrilateral. Students can practice the questions of quadrilateral worksheet before the examinations to get more confident.

1. Fill in the blanks: 

  (i) A quadrilateral has …………… sides. 

  (ii) A quadrilateral has …………… angles. 

  (iii) A quadrilateral has …………… vertices, no three of which are ………… . 

  (iv) A quadrilateral has …………… diagonals. 

  (v) A diagonal of a quadrilateral is a line segment that joins two ……………… vertices of the quadrilateral. 

  (vi) The sum of the angles of a quadrilateral is ……………… . 

2. Multiple Choice Question (MCQ) on Quadrilaterals: 

   Tick (✔) the correct option.

(i) Two sides of a quadrilateral are said to be opposite sides, if they

(a) have a common end-point.;     (b) are adjacent sides.;     (c) are not adjacent sides.;     (d) none of the above.

3. Take a point O inside a pentagon ABCDE. Join the point O with all its vertices. In how many triangles will the pentagon be divided? Name them.

4. Draw a quadrilateral. Name the sides, vertices, angles and diagonals of the quadrilateral.

5. From the following figure, name:

(i) the pairs of adjacent sides.

(ii) the pairs of opposite sides.

(iii) the pairs of adjacent angles.

(iv) the pairs of opposite angles.

6. In the adjoining figure, ABCD is a quadrilateral. 

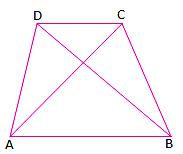
  (i) How many pairs of adjacent sides are there? Name them.

  (ii) How many pairs of opposite sides are there? Name them.

  (iii) How many pairs of adjacent angles are there? Name them.

  (iv) How many pairs of opposite angles are there? Name them.

  (v) How many diagonals are there? Name them.

7. Name the quadrilateral that satisfies the description:

(i) Opposite sides are parallel. All sides are equal.

(ii) One angle equals 90°. Opposite sides are parallel.

(iii) Two sides are parallel. Other two sides are not parallel.

(iv) All sides are equal. All angles are equal.

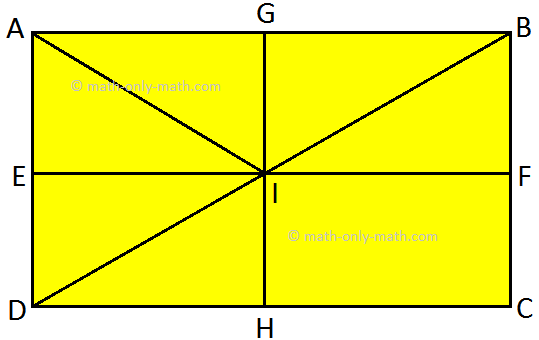
8. Find the number of rectangles in the following figure and name them.

9. Which of the following is/are 'true' or 'false' in case of a square?

(i) Sum of adjacent angles is 360°.

(ii) Diagonals bisect each other.

(iii) Opposite sides are parallel and equal.

(iv) Adjacent sides are not equal.

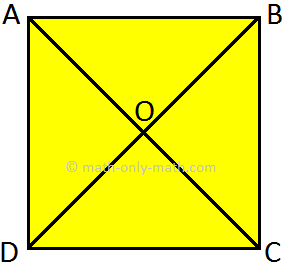
10. In the following figure, a square ABCD is given. State whether the following statements are true or false:

(i) AB = BC

(ii) CD || AD

(iii) ∠DAB = ∠BCD

(iv) ∠AOB = 90°

(v) AO = OC

11. Make the following statements true using the terms 'All', 'Some' or 'No':

(i) __________ rhombuses are squares.

(ii) __________ trapeziums are quadrilaterals.

(iii) __________ squares are rhombuses.

(iv) __________ parallelograms are also trapeziums.

(ν) __________ trapeziums are isosceles.

(vi) __________ parallelograms are also quadrilaterals.

12. Prove that the sum of the angles of a quadrilateral is 360°.

13. The three angles of a quadrilateral are 76°, 54° and 108°. Find the measure fourth angle.

14. The angles of a quadrilateral are in the ratio 3 : 5 : 7 : 9. Find the measure of each of these angles.

15. A quadrilateral has three acute angles, each measuring 75°. Find the measure of the fourth angle.

16. Three angles of a quadrilateral are equal and the measure of the fourth angle is 120°. Find the measure of each of the equal angles.

17. Two angles of a quadrilateral measure 85° and 75° respectively. The other two angles equal. Find the measure of each of these equal angles.

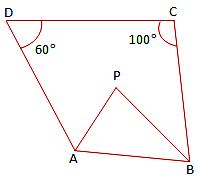
18. In the adjacent figure, the bisectors of ∠A and ∠B meet in a point P.
If ∠C = 1000 and ∠D = 60°, find the measure of ∠APB.

Hint: 60° + 100° + ∠A + ∠B = 360°

⇒ ∠A + ∠B = 200°

⇒ ¹/₂ ∠A + ¹/₂ ∠B = 100°

⇒ ∠BAP + ∠ABP = 100°

But, ∠BAP + ∠ABP + ∠APB = 180° (why?)

Now, find ∠APB.

Answers for quadrilateral worksheet are given below to check the exact answers of the above questions.

Quadrilateral Worksheet Answers:

1. (i) four

(ii) four

(iii) four, collinear

(iv) two

(v) opposite

(vi) 360°

2. (i) → (c) are not adjacent sides.

3. 23

4. Draw a quadrilateral. Name the sides, vertices, angles and diagonals of the quadrilateral.

5. (i) (AB, BC); (BA, AD); (AD, DC); (DC, CB)

(ii) (AB, DC); (AD, BC)

(iii) (∠A, ∠B); (∠A, ∠D); (∠D, ∠C); (∠C, ∠B)

(iv) (∠A, ∠C); (∠B, ∠D)

6. (i) four; (AB, BC), (BC, CD), (CD, DA), (DA, AB)

(ii) two; (AB, DC), (AD, BC)

(iii) four; (∠A, ∠B), (∠B, ∠C), (∠C, ∠D), (∠D, ∠A)

(iv) two; (∠A, ∠C), (∠B, ∠D)

(v) two; (AC, BD)

7. (i) Rhombus Square

(ii) Rectangle Square

(iii) Trapezium

(iv) Square

8. ABCD, AGIE, GBFI, FCHI, HDEI, AGHD, GBCH, ABFE, EFCD

9. (i) False

(ii) True

(iii) True

(iv) False

10. (i) True

(ii) False

(iii) True

(iv) True

(v) True

11. (i) Some

(ii) All

(iii) All

(iv) No

(ν) Some

(vi) All

12. 

13. 122°

14. 45°, 75°, 105°, 135°

15. 135°

16. 80o

17. 100°

18. 80°

● Quadrilateral

What is Quadrilateral?

Different Types of Quadrilaterals

Construction of Quadrilaterals

Construct Different Types of Quadrilaterals

● Quadrilateral - Worksheets

Quadrilateral Worksheet

Worksheet on Construction on Quadrilateral

Worksheet on Different Types of Quadrilaterals

8th Grade Math Practice

From Quadrilateral Worksheet to HOME PAGE