Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Fundamental Geometrical Concepts
The fundamental geometrical concepts depend on three basic concepts — point, line and plane. The terms cannot be precisely defined. However, the meanings of these terms are explained through examples.
Point:
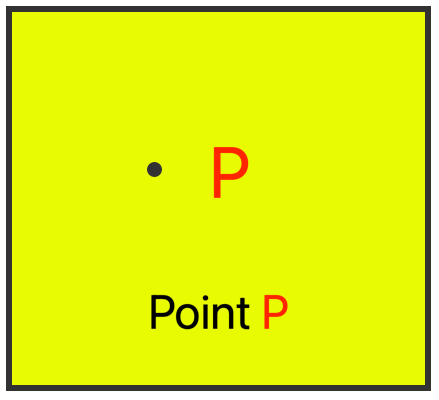
Take a fine pencil and mark a dot with it on paper. Call it P. We say that P is a point.
Thus, a dot represents a point.
|
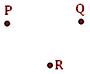
Properties of Point: ● It is the mark of position and has an exact location. ● It has no length, breadth or thickness. ● It is denoted by a dot made by the tip of a sharp pencil. ● It is denoted by capital letter. ● In the given figure P, Q, R represents different points. |
Thus, a small dot made by a sharp pencil on a piece of paper represents a point. ● A
A point has no length, no breadth and no thickness. It has only position, A point is named by a single capital letter such as A, B, C, etc.
Line:
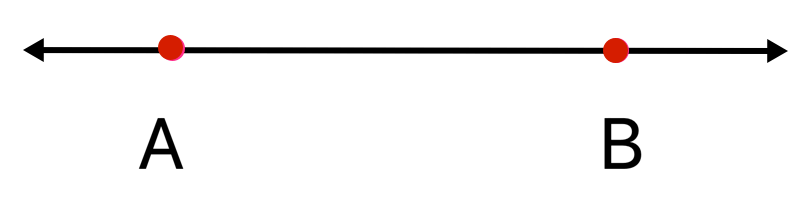
In the figure, AB is a straight line.
★ A line can be extended to any length on both the sides.
★ A line has no end-points.
★ A line has no length.
Is line AB the same as line BA? Yes
A line is sometimes named by a single letter.
In the above figure ℓ is the line.
Properties of Line:
● It is a straight path which can be extended indefinitely in both the directions.
● It is shown by two arrowheads in opposite directions.
● It does not have any fixed length.
● It has no endpoints.
● It is denoted as \(\overleftrightarrow{AB}\) or \(\overleftrightarrow{BA}\) and is read as line AB or line in the BA.
● It can never be measured.
● Infinite number of points lie on the line.
● Sometimes it is also denoted by small letters of the English alphabet.
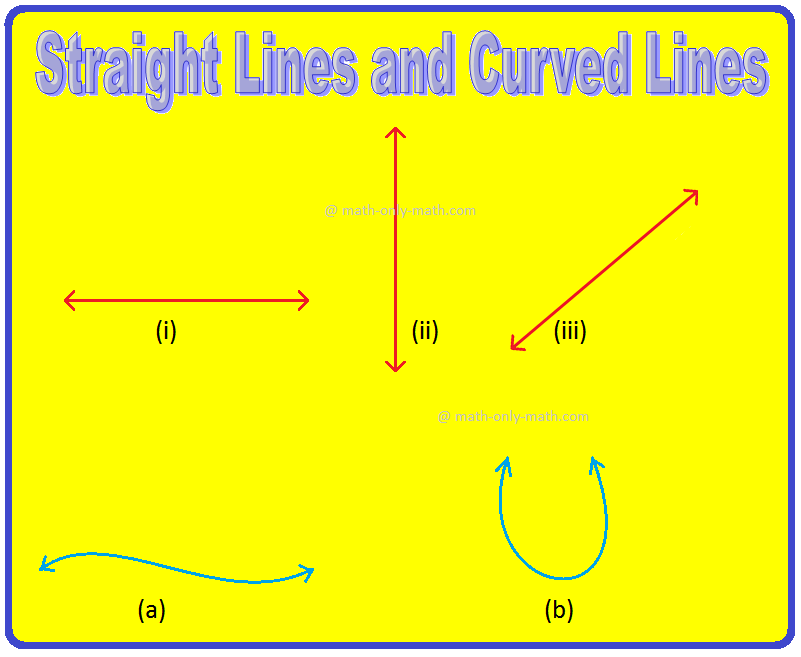
There are two types of lines: straight line and curved line.
Lines (i), (ii), (iii) are straight lines.
Lines (a) and (b) are curved lines.
To understand the idea of a line, let us perform the following activities:
Activity I:
|
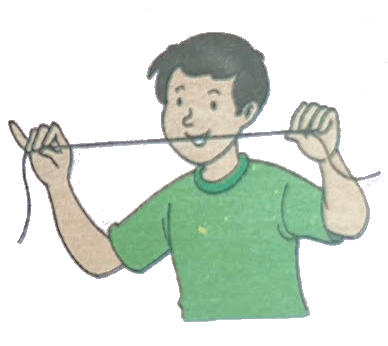
Take a thread. Take one end of it in one hand and the other end in the another hand. Stretch the thread straight. We say that it forms a straight line. |
|
Now, loose the thread. What do we observe? The straight thread now becomes curved. This gives the concept of a curved line. |
Activity II:
|
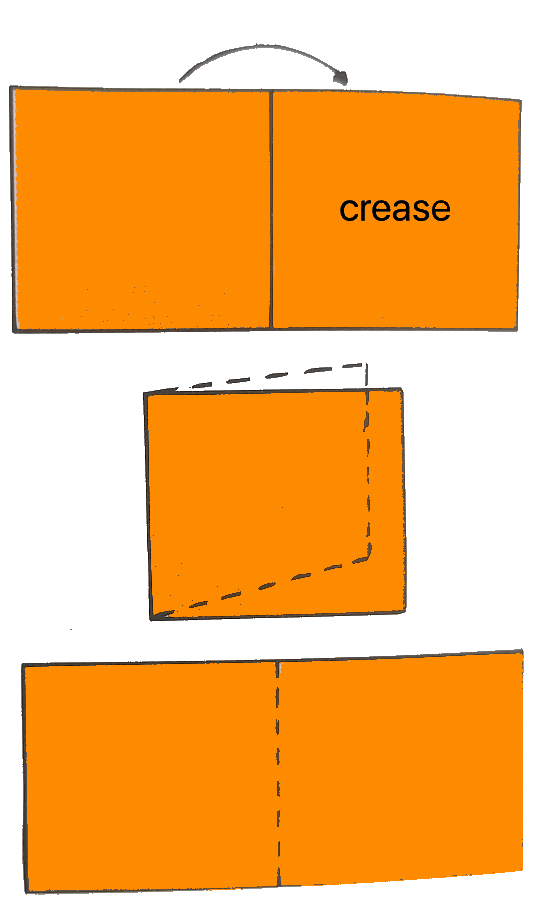
Take a piece of paper. Fold it along the middle. Press the fold firmly. Open up the folded paper and observe the crease in the middle of the paper. This crease on the paper gives an idea of a straight line. |
|
Examples of Straight Lines |
Examples of curved lines |
|
The edges of a blackboard, the edges of the table top, and edge of a stick are some examples of straight lines. |
Lines obtained by drawing along the edge of a bangle, coins etc. are examples of curved lines. |
Ray:
A line segment extended endlessly in one direction only is called a ray.
It has one end point.
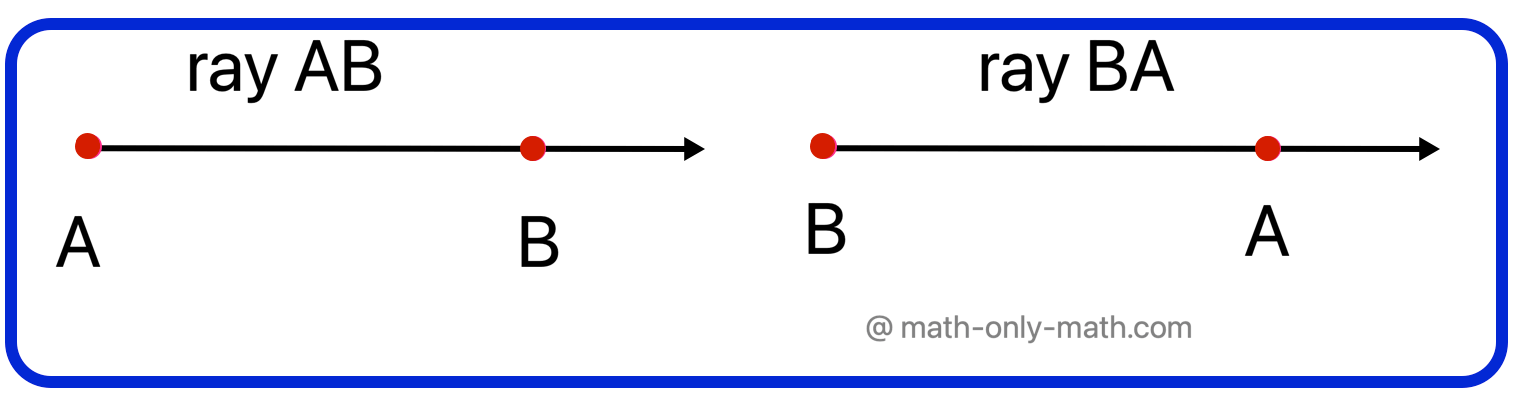
In figure, AB is a ray whose end-point is A.
It is denoted by \(\overrightarrow{AB}\).
Point A is also called the initial point of \(\overrightarrow{AB}\).
A ray has no definite length.
Note that while naming a ray we start with the initial point, that is ray AB (\(\overrightarrow{AB}\)) which is different from ray BA (\(\overrightarrow{BA}\)).
Properties of Ray:
● It is a straight path which can be extended indefinitely in one direction only and the other end is fixed.
● It has no fixed length.
● It has one endpoint called the initial point.
● It cannot be measured.
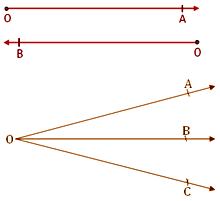
● It is denoted as \(\overrightarrow{OA}\) and is read as ray OA.
● A number of rays can be drawn from an initial point O.
● Ray OA and ray OB are different because they are extended in different directions.
● Infinite points lie on the ray.
Line Segment:
Mark any two points A and B on a sheet of paper and join A to B.
The straight path from A to B is called the line segment AB.
A line segment has a fixed length.
Line segment AB is denoted as \(\overline{AB}\).
The points A and B are called end-points of \(\overline{AB}\).
The distance between the points A and B is called the length of \(\overline{AB}\).
Line segment AB is the same as line segment BA.
Properties of Ray:
● It is a straight path which has a definite length.
● It has two endpoints.
● It is a part of the line.
● It is denoted as AB or BA.
● It is read as line segment AB or line segment BA.
● The distance between A and B is called the length of AB.
● Infinite number of points lies on a line segment.
● Two line segments are said to be equal if they have the same length.
Plane:
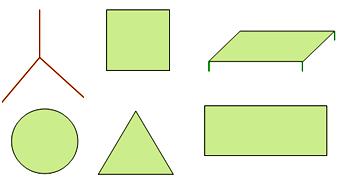
A smooth, flat surface gives us an idea of a plane. The surface of the table, wall, blackboard, etc., is smooth and flat. It extends endlessly in all the directions. It has no length, breadth or thickness. Here, we have shown a portion of a particular plane. We can draw certain figures like square, rectangle, triangle, and circle on the plane. Hence, these figures are also called plane figures.
Incidence Properties of Lines in a Plane:
● An infinite number of many lines can be drawn to pass through a given point in a plane.
Through a given point in a plane, infinitely many lines can be drawn to pass through.
● Two distinct points in a plane determine a unique line.
One and only one line can be drawn to pass through two given points, i.e., two distinct points in a plane. This line lies wholly in the plane.
● Infinite number of points lie on the line in a plane.
● Two lines in a plane either intersect at a point or they are parallel to each other.
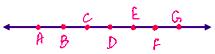
Collinear Points:
Two or more points which lie on the same line in a plane are called collinear points.
Properties of Collinear Points:
● The line is called the line of colinearity.
● Two points are always collinear.
● In the adjoining figure………
Points A, B, C are collinear lying on line
Points X, Y, Z are not collinear because all the three points do not lie on a line.
Hence, they are called non-collinear points.
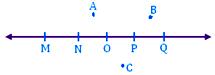
Similarly, here points M, N, O, P, Q are collinear points and A, B, C are non-collinear points.
Note:
Two points are always collinear.
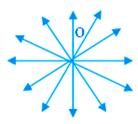
Concurrent Lines:
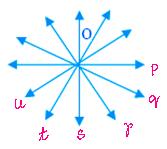
Three or more lines which pass through the same point are called concurrent lines and this common point is called the point of concurrence. In the adjoining figure, lines p, q, r, s, t, u intersect at point O and are called concurrent lines.
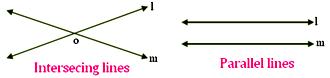
Two lines in a Plane:
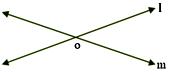
Intersecting Lines: Two lines in a plane which cut each other at common point are called intersecting lines and the point is called the point of intersection. In the adjoining figure, lines l and m intersect at point O.
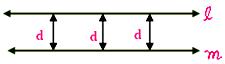
Parallel Lines: Two lines in a plane which do not intersect at any point, i.e., they do not have any point in common are called parallel lines. The distance between the two parallel lines remains the same throughout.
These are the fundamental geometrical concepts explained above using figures.
Worksheet on Fundamental Geometrical Concepts:
1. State true or false:
(i) Ray AB is different from ray BA.
(ii) A point has no length no breadth and no thickness.
(iii) A ray has no definite length.
(iv) A line segment has no definite length.
(v) A line has two end points.
Answer:
1. (i) true
(ii) true
(iii) true
(iv) false
(v) false
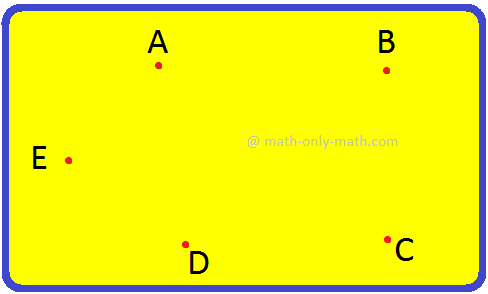
2. Given here are 5 different points. Draw line segments by joining.
3. How many line segments are there in this figure?
Name them:
● Lines and Angles
Fundamental Geometrical Concepts
Some Geometric Terms and Results
Complementary and Supplementary Angles
Parallel and Transversal Lines
7th Grade Math Problems
8th Grade Math Practice
From Fundamental Geometrical Concepts to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.







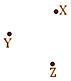


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.