Subscribe to our YouTube channel for the latest videos, updates, and tips.
Properties of Parallel Lines
What are Parallel Lines?
Two lines in a plane are said to be parallel if they do not intersect, when extended infinitely in both the direction.
Also, the distance between the two lines is the same throughout.
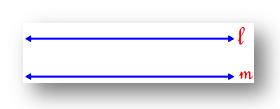
Parallel Lines
The symbol for denoting parallel lines is ∥.
If lines l and m are parallel to each other, we can write it as l∥m and which is read as ‘l is parallel to m’.
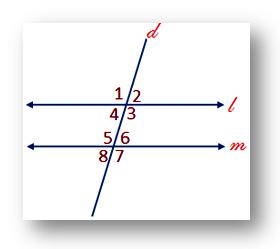
Properties Of Angles Associated with Parallel Lines:
If two parallel lines are cut by a transversal, then
• the pair of corresponding angles is equal (∠2 = ∠6); (∠3 = ∠7); (∠1 = ∠5); (∠4 = ∠8).
• the pair of interior alternate angles is equal (∠4 = ∠6); (∠3 = ∠5).
• the pair of exterior alternate angles is equal (∠1 = ∠7); (∠2 = ∠8).
• interior angles on the same side of transversal are supplementary, i.e.,
∠3 + ∠6 = 180° and ∠4 + ∠5 = 180°.
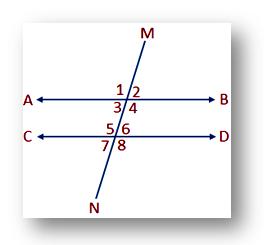
For example let us observe, the adjacent figure shows two parallel straight lines AB and CD.
When two parallel lines AB and CD are cut by a transversal MN.
(i) Interior and exterior alternate angles are equal.
i.e. ∠3 = ∠6 and ∠4 = ∠5 [Interior alternate angles]
∠1 = ∠8 and ∠2 = ∠7 [Exterior alternate angles]
(ii) Corresponding angles are equal.
i.e. ∠1 = ∠5; ∠2 = ∠6; ∠3 = ∠7 and ∠4 = ∠8
(iii) Co-interior or allied angles are supplementary.
i.e. ∠3 + ∠5 = 180° and ∠4 + ∠6 = 180°
Conditions of Parallelism:
If two straight lines are cut by a transversal, and if
• the pair of corresponding angles is equal, then the two straight lines are parallel to each other.
• the pair of alternate angles is equal, then the two straight lines are parallel to each other.
• the pair of interior angles on the same side of transversal is supplementary, then the two straight lines are parallel.
Therefore, in order to prove that the given lines are parallel; show either alternate angles are equal or, corresponding angles are equal or, the co-interior angles are supplementary.
Parallel Rays:
Two rays are parallel if the corresponding lines determined by them are parallel. In other words, two rays in the same plane are parallel if they do not intersect each other even if extended indefinitely beyond their initial points.
Parallel Rays
Therefore, ray AB ∥ ray MN
Parallel Segments:
Two segments are parallel if the corresponding lines determined by them are parallel.
In other word, two segments which are in the same plane and do not intersect each other even if extended indefinitely in both directions are said to be parallel.
Parallel Segments
Therefore, segment AB ∥ segment MN
One segment and one ray are parallel if the corresponding lines determined by them are parallel.
Therefore, segment AB ∥ ray PQ.
The opposite edge of a ruler is an example of parallel line segments.
● Lines and Angles
Fundamental Geometrical Concepts
Some Geometric Terms and Results
Complementary and Supplementary Angles
Parallel and Transversal Lines
7th Grade Math Problems
8th Grade Math Practice
From Properties of Parallel Lines to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Conversion of Temperature | Temperature Worksheets | Ans
Jun 24, 25 02:20 AM
We will practice the questions given in the worksheet on conversion of temperature from one scale into another. We know the two different temperature scales are the Fahrenheit scale and the -
Worksheet on Temperature |Celsius to Fahrenheit, Fahrenheit to Celsius
Jun 24, 25 01:58 AM
In the worksheet on temperature we will solve 10 different types of questions.1. Which is colder 32°F or 0°C? 2. Water boils at ...°C and freezes at ....°F. -
5th Grade Temperature | Fahrenheit Scale | Celsius Scale | Thermometer
Jun 24, 25 12:28 AM
We will discuss here about the concept of temperature. We have already learned about various types of measurements like length, mass capacity and time. But if we have fever, non of these measurements -
Converting the Temperature from Fahrenheit to Celsius | Examples
Jun 20, 25 12:53 PM
In converting the temperature from Fahrenheit to Celsius the formula is, C = (5/9)(F - 32); The steps of converting from Fahrenheit to Celsius are reversed here. -
Converting the Temperature from Celsius to Fahrenheit | Examples
Jun 20, 25 12:01 PM
In converting the temperature from Celsius to Fahrenheit the formula is F = (9/5)C + 32. Steps of converting from Celsius (°C) to Fahrenheit (°F)
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.