Parallel and Transversal Lines



Here we discuss how the angles formed between parallel and transversal lines.



When the transversal intersects two parallel lines:

• Pairs of corresponding angles are equal.

• Pairs of alternate angles are equal

• Interior angles on the same side of transversal are supplementary.


Worked-out problems for solving parallel and transversal lines:

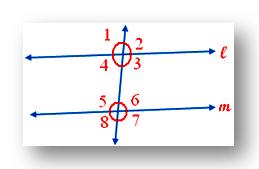
1. In adjoining figure l ∥ m is cut by the transversal t. If ∠1 = 70, find the measure of ∠3, ∠5, ∠6.

two parallel lines are cut by the transversal

Solution:

We have ∠1 = 70°
∠1 = ∠3 (Vertically opposite angles)
Therefore, ∠3 = 70°

Now, ∠1 = ∠5 (Corresponding angles)
Therefore, ∠5 = 70°

Also, ∠3 + ∠6 = 180° (Co-interior angles)
70° + ∠6 = 180°
Therefore, ∠6 = 180° - 70° = 110°


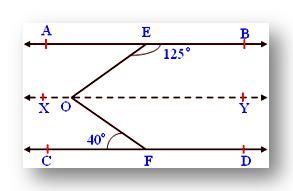
2. In the given figure AB ∥ CD, ∠BEO = 125°, ∠CFO = 40°. Find the measure of ∠EOF.

Solution:

parallel and transversal lines



Draw a line XY parallel to AB and CD passing through O such that AB ∥ XY and CD ∥ XY

∠BEO + ∠YOE = 180° (Co-interior angles)
Therefore, 125° + ∠YOE = 180°

Therefore, ∠YOE = 180° - 125° = 55°

Also, ∠CFO = ∠YOF (Alternate angles)

Given ∠CFO = 40°
Therefore, ∠YOF = 40°

Then ∠EOF = ∠EOY + ∠FOY
= 55° + 40° = 95°



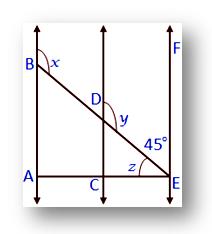
3. In the given figure AB ∥ CD ∥ EF and AE ⊥ AB.
Also, ∠BAE = 90°. Find the values of ∠x, ∠y and ∠z.

Solution:

parallel and transversal



y + 45° = 1800
Therefore, ∠y = 180° - 45° (Co-interior angles)
= 135°

∠y =∠x (Corresponding angles)
Therefore, ∠x = 135°

Also, 90° + ∠z + 45° = 180°
Therefore, 135° + ∠z = 180°

Therefore, ∠z = 180° - 135° = 45°


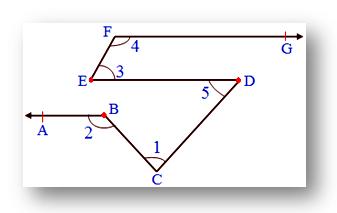
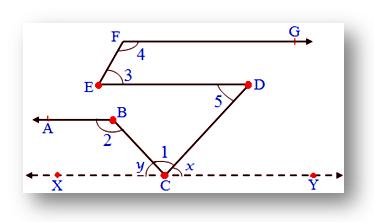
4. In the given figure, AB ∥ ED, ED ∥ FG, EF ∥ CD
Also, ∠1 = 60°, ∠3 = 55°, then find ∠2, ∠4, ∠5.

Solution:

transversal intersects two parallel lines



Since, EF ∥ CD cut by transversal ED
Therefore, ∠3 = ∠5 we know, ∠3 = 55°
Therefore, ∠5 = 55°

Also, ED ∥ XY cut by transversal CD
Therefore, ∠5 = ∠x we know ∠5 = 55°

Therefore,∠x = 55°

Also, ∠x + ∠1 + ∠y = 180°
55° + 60° + ∠y = 180°
115° + ∠y = 180°
∠y = 180° - 115°
Therefore, ∠y = 65°

Now, ∠y + ∠2 = 1800 (Co-interior angles)

Parallel and transversal image



65° + ∠2 = 180°
∠2 = 180° - 65°
∠2 = 115°

Since, ED ∥ FG cut by transversal EF

Therefore, ∠3 + ∠4 = 180°
55° + ∠4 = 180°
Therefore, ∠4 = 180° - 55° = 125°


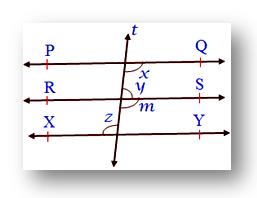
5. In the given figure PQ ∥ XY. Also, y : z = 4 : 5 find.

Parallel and transversal lines image


Solution:

Let the common ratio be a
Then y = 4a and z = 5a
Also, ∠z = ∠m (Alternate interior angles)

Since, z = 5a
Therefore, ∠m = 5a [RS ∥ XY cut by transversal t]

Now, ∠m = ∠x (Corresponding angles)
Since, ∠m = 5a
Therefore, ∠x = 5a [PQ ∥ RS cut by transversal t]

∠x + ∠y = 180° (Co-interior angles)

5a + 4a = 1800
9a = 180°
a = 180/9
a = 20

Since, y = 4a
Therefore, y = 4 × 20
y = 80°

z = 5a
Therefore, z = 5 × 20
z = 100°

x = 5a
Therefore, x = 5 × 20
x = 100°

Therefore, ∠x = 100°, ∠y = 80°, ∠z = 100°



● Lines and Angles

  • Fundamental Geometrical Concepts
  • Basic Geometrical Concepts
  • Angles
  • Classification of Angles
  • Related Angles
  • Some Geometric Terms and Results
  • Complementary Angles
  • Supplementary Angles
  • Complementary and Supplementary Angles
  • Adjacent Angles
  • Linear Pair of Angles
  • Vertically Opposite Angles
  • Parallel Lines
  • Transversal Line
  • Parallel and Transversal Lines

    • 7th Grade Math Problems

    8th Grade Math Practice

    From Parallel and Transversal Lines to HOME PAGE

    © and ™ math-only-math.com. All Rights Reserved. 2010 - 2012.