Subscribe to our YouTube channel for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Complementary Angles
When the sum of the measures of two angles is 90°, such angles are called complementary angles and each angle is called a complement of the other.
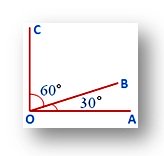
The vertices of two angles may be same or different. In the given figure ∠AOB and ∠BOC are complementary as ∠AOB + ∠BOC = 30° + 60° = 90°.
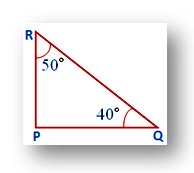
Again, ∠PQR and ∠QRP are complementary as ∠PQR + ∠QRP = 40° + 50° = 90°.
Angles of measure 25° and 65° are complementary angles. The angle of 25° is the complement of the angle of 65° and the angle of 65° is the complement of the angle of 25°.
The complement of an angle of measure 32° is the angle of 58°. And, the complement of the angle of measure 58° is the angle of 32°.
Observations:
(i) If two are complement of each other, then each is an acute angle. But any two acute angles need not be complementary.
For example, angles of measure 30° and 50° are not complement of each other.
(ii) Two obtuse angles cannot be complement of each other.
(iii) Two right angles cannot be complement of each other.
Worked-out Problems on Complementary Angles:
1. Find the complement of:
(a) 68°
Solution:
90° - 68°
= 22°
Therefore, the complement of 68° is 22°
(b) 27°20'
Solution:
90° - 27°20'
= 89°60' - 27°20'
= 62°40'
Therefore, the complement of 27°20' is 62°40'
(c) x + 52°
Solution:
90° - (x + 52°)
= 90° - x + 52°
= 38° - x
Therefore, the complement of x + 52° is 38° - x
2. Find the complement of the angle (10 + y)°.
Solution:
Complement of the angle (10 + y)° = 90° - (10 + y)°
= 90° - 10° - y°
= (80 - y)°
3. Find the measure of an angle which is 46° less than its complement.
Solution:
Let the unknown angle be x, then measure of its complement = 90 - x
According to the question,
(90 - x) - x = 46°
90 - x - x = 46°
90 - 2x = 46°
90 - 90 - 2x = 46° - 90
-2x = 46° - 90
-2x = 46° - 90
-2x = -44°
2x = 44°
x = 44/2
x = 22°
Therefore, 90 - x (Put the value of x = 22°)
= 90 - 22°
= 68°
Therefore, the pair of complementary angles are 68° and 22°
● Lines and Angles
Fundamental Geometrical Concepts
Some Geometric Terms and Results
Complementary and Supplementary Angles
Parallel and Transversal Lines
7th Grade Math Problems
8th Grade Math Practice
From Complementary Angles to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
5th Grade Circle Worksheet | Free Worksheet with Answer |Practice Math
Jul 11, 25 02:14 PM
In 5th Grade Circle Worksheet you will get different types of questions on parts of a circle, relation between radius and diameter, interior of a circle, exterior of a circle and construction of circl… -
Construction of a Circle | Working Rules | Step-by-step Explanation |
Jul 09, 25 01:29 AM
Construction of a Circle when the length of its Radius is given. Working Rules | Step I: Open the compass such that its pointer be put on initial point (i.e. O) of ruler / scale and the pencil-end be… -
Combination of Addition and Subtraction | Mixed Addition & Subtraction
Jul 08, 25 02:32 PM
We will discuss here about the combination of addition and subtraction. The rules which can be used to solve the sums involving addition (+) and subtraction (-) together are: I: First add -
Addition & Subtraction Together |Combination of addition & subtraction
Jul 08, 25 02:23 PM
We will solve the different types of problems involving addition and subtraction together. To show the problem involving both addition and subtraction, we first group all the numbers with ‘+’ and… -
5th Grade Circle | Radius, Interior and Exterior of a Circle|Worksheet
Jul 08, 25 09:55 AM
A circle is the set of all those point in a plane whose distance from a fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is known
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.