Supplementary Angles
When the sum of the measures of two angles is 180°, such angles are called supplementary angles and each of them is called a supplement of the other.
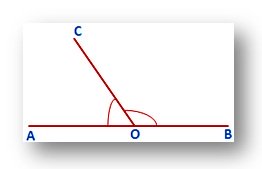
The vertices of two angles may be same or different. In the given figure ∠AOC and ∠BOC are supplementary angles as ∠AOC + ∠BOC = 180°.
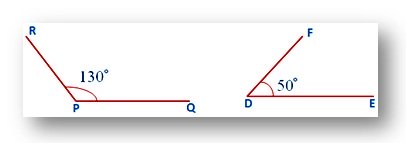
Again, ∠QPR and ∠EDF are supplementary angles as ∠QPR + ∠EDF = 130° + 50° = 180°.
Angles of 60° and 120° are supplementary angles.
The supplement of an angle of 110° is the angle of 70° and the supplement of an angle of 70° is the angle of 110°
Observations:
(i) Two acute angles cannot be supplement of each other.
(ii) Two right angles are always supplementary.
(iii) Two obtuse angles cannot be supplement of each other.
Worked-out Problems on Supplementary Angles:
1. Verify if 115°, 65° are a pair of supplementary angles.
Solution:
115° + 65° = 180°
Hence, they are a pair of supplementary angles.
2. Find the supplement of the angle (20 + y)°.
Solution:
Supplement of the angle (20 + y)° = 180° - (20 + y)°
= 180° - 20° - y°
= (160 - y) °
3. If angles of measures (x — 2)° and (2x + 5)° are a pair of supplementary angles. Find the measures.
Solution:
Since (x - 2)° and (2x + 5)° represent a pair of supplementary angles, then their sum must be equal to 180°.
Therefore, (x - 2) + (2x + 5) = 180
x - 2 + 2x + 5 = 180
x + 2x - 2 + 5 = 180
3x + 3 = 180
3x + 3 – 3 = 180 — 3
3x = 180 — 3
3x = 177
x = 177/3
x = 59°
Therefore, we know the value of x = 59°, put the value in place of x
x - 2
= 59 - 2
= 57°
And again, 2x + 5
= 2 × 59 + 5
= 118 + 5
= 123°
Therefore, the two supplementary angles are 57° and 123°.
4. Two supplementary angles are in the ratio 7 : 8. Find the measure of the angles.
Solution:
Let the common ratio be x.
If one angle is 7x, then the other angle is 8x.
Therefore, 7x + 8x = 180
15x = 180
x = 180/15
x = 12
Put the value of x = 12
One angle is 7x
= 7 × 12
= 84°
And the other angle is 8x
= 8 × 12
= 96°
Therefore, the two supplementary angles are 84° and 96°.
5. In the given figure find the measure of the unknown angle.
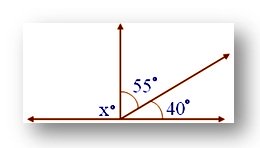
Solution:
x + 55° + 40° = 180°
The sum of angles at a point on a line on one side of it is 180°
Therefore, x + 95° = 180°
x + 95° - 95° = 180° - 95°
x = 85°
● Lines and Angles
Fundamental Geometrical Concepts
Some Geometric Terms and Results
Complementary and Supplementary Angles
Parallel and Transversal Lines
8th Grade Math Practice
From Supplementary Angles to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
|
|
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.