How to Find the Average in Math?

Average means a number which is between the largest and the smallest number.

We often hear words like average marks, average speed, average income, etc. In fact, average is a very common term, we use in our day-to-day life

An average is a number which is used to represent each one of many in general.

Let us understand the concept of average by taking an example.

Suppose, five boys James, Thomas, David, John and Matthew weigh 30 kg, 35 kg, 40 kg, 25 kg and 30 kg respectively. This means, their total weight is (30 + 35 + 40 + 25 + 30) kg = 160 kg. If we divide this by the total number of boys i.e., 5, we get 32 kg as the result. This is called the average weight of the boys.

To find the average of the given quantities, we add the quantities and divide the sum by the total number of quantities

Average = $\frac{\textbf{Sum of the given Quantities}}{\textbf{Number of Quantities}}$

For example:

Teacher: Children, come one by one and pick up some toffees from the box.

Ron: I have got 8 toffees.

Shelly: I have got 2 toffees.

Mary: I have got 1 toffee.

Teacher: Don’t worry! let me distribute these 24 toffees equally among you.

We divide 24 by 4;

24 ÷ 4 = 6

Thus we observe that on an average each child gets 6 toffees

Or

We can say that the average number of toffees each child gets is 6.

To find the average of a group of numbers, divide the sum of numbers by the total number of events.

Average = Sum of events by total number of events.

Average can be calculated only for similar quantities and not for dissimilar quantities.

Average of height and weight cannot be calculated. It should either be average height of all students or average weight of all students.

The formulas of solving average,

Solved examples on finding the average of different set of of numbers:

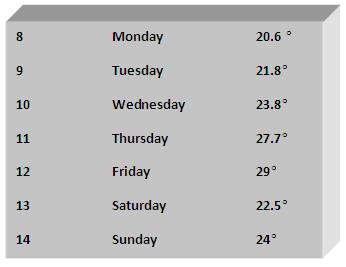
1. The maximum temperature of Miami during 8th September to 14th September is as follows:

Solution:

We know, Average = (Sum of all items)/(Number of items)

The average temperature of this week in Miami

= (20.6 + 21.8 + 23.8 + 27.7 + 29 + 22.5 + 24)/7

= 169.4/7

= 24.2°

2. Find the average of 5, 7, 6, 8, 4, 9

Solution:

Sum of the given number = 5 + 7 + 6 + 8 + 4 + 9 = 39

Number of events = 6

Therefore, average of numbers = 39/6 = 13/2 = 6.5

3. Find the average of 3.6, 2.7, 4.1, 1.5, and 5.3.

Solution:

Sum of the numbers = 3.6 + 2.7 + 4.1 + 1.5 + 5.3 = 17.2

Number of events = 5.

Average of numbers = 17.2/5 = 3.44

4. The marks obtained by Sara in the first three Unit Tests in Maths are 85, 89 and 98.

Solution:

Sara’s average marks in Maths Unit Tests are = (85 + 89 + 98)/3

= 272/3

= 90.6

Thus, Sara’s average marks in Maths Unit Tests = 90.6 %.

5. The average consumption of wheat by a family is 33 kgs in three months. If there are 15 members in the family, find the total consumption for three months.

Solution:

Average = 33 kgs.

No. of members = 15

Total = Average × No. of members.

= 33 × 15

= 495 kg.

Therefore, the total consumption of wheat for 3 months is 495 kg.

6. Total height of a class is 1300 cm. If the average height of a class is 65 cm, find the number of students in the class.

Solution:

Total height of a class = 1300 cm.

Average = 65 cm.

No. of students = Total ÷ Average

= 1300 ÷ 65

= 20

Therefore, number of students in the class = 20

● Average.

Word Problems on Average

Worksheet on Average.

Worksheet on word Problems on Average

5th Grade Numbers

5th Grade Math Problems

From How to Find the Average? to HOME PAGE