Complementary and Supplementary Angles

Before we solve the worked-out problems on complementary and supplementary angles we will recall the definition of complementary angles and supplementary angles.

Complementary Angles:

Two angles are called complementary angles, if their sum is one right angle i.e. 90°.

Each angle is called the complement of the other. 

Example, 20° and 70° are complementary angles, because 20° + 70° = 90°.

Clearly, 20° is the complement of 70° and 70° is the complement of 20°.

Thus, the complement of angle 53° = 90° - 53° = 37°.

Supplementary Angles:

Two angles are called supplementary angles, if their sum is two right angles i.e. 180°.

Each angle is called the supplement of the other. 

Example, 30° and 150° are supplementary angles, because 30° + 150° = 180°.

Clearly, 30° is the supplement of 150° and 150° is the supplement of 30°.

Thus, the supplement of angle 105° = 180° - 105° = 75°.

Solved problems on complementary and supplementary angles:

1. Find the complement of the angle 2/3 of 90°.

Solution:

Convert 2/3 of 90°

2/3 × 90° = 60°

Complement of 60° = 90° - 60° = 30°

Therefore, complement of the angle 2/3 of 90° = 30°

2. Find the supplement of the angle 4/5 of 90°.

Solution:

Convert 4/5 of 90°

4/5 × 90° = 72°

Supplement of 72° = 180° - 72° = 108°

Therefore, supplement of the angle 4/5 of 90° = 108°

3. The measure of two complementary angles are (2x - 7)° and (x + 4)°. Find the value of x.

Solution:

According to the problem, (2x - 7)° and (x + 4)°, are complementary angles’ so we get;

(2x - 7)° + (x + 4)° = 90°

or, 2x - 7° + x + 4° = 90°

or, 2x + x - 7° + 4° = 90°

or, 3x - 3° = 90°

or, 3x - 3° + 3° = 90° + 3°

or, 3x = 93°

or, x = 93°/3°

or, x = 31°

Therefore, the value of x = 31°.

4. The measure of two supplementary angles are (3x + 15)° and (2x + 5)°. Find the value of x.

Solution:

According to the problem, (3x + 15)° and (2x + 5)°, are complementary angles’ so we get;

(3x + 15)° + (2x + 5)° = 180°

or, 3x + 15° + 2x + 5° = 180°

or, 3x + 2x + 15° + 5° = 180°

or, 5x + 20° = 180°

or, 5x + 20° - 20° = 180° - 20°

or, 5x = 160°

or, x = 160°/5°

or, x = 32°

Therefore, the value of x = 32°.

5. The difference between the two complementary angles is 180°. Find the measure of the angle.

Solution:

Let one angle be of measure x°.

Then complement of x° = (90 - x)

Difference = 18°

Therefore, (90° - x) – x = 18°

or, 90° - 2x = 18°

or, 90° - 90° - 2x = 18° - 90°

or, -2x = -72°

or, x = 72°/2°

or, x = 36°

Also, 90° - x

= 90° - 36°

= 54°.

Therefore, the two angles are 36°, 54°.

6. POQ is a straight line and OS stands on PQ. Find the value of x and the measure of ∠ POS, ∠ SOR and ∠ ROQ.

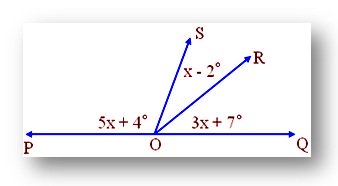
Solution:

POQ is a straight line.

Therefore, ∠POS + ∠SOR + ∠ROQ = 180°

or, (5x + 4°) + (x - 2°) + (3x + 7°) = 180°

or, 5x + 4° + x - 2° + 3x + 7° = 180°

or, 5x + x + 3x + 4° - 2° + 7° = 180°

or, 9x + 9° = 180°

or, 9x + 9° - 9° = 180° - 9°

or, 9x = 171°

or, x = 171/9 

or, x = 19°

Put the value of x = 19°

Therefore, x - 2

= 19 - 2

= 17°

Again, 3x + 7

= 3 × 19° + 7°

= 570 + 7°

= 64°

And again, 5x + 4

= 5 × 19° + 4°

= 95° + 4°

= 99°

Therefore, the measure of the three angles is 17°, 64°, 99°.

These are the above solved examples on complementary and supplementary angles explained step-by-step with detailed explanation.

● Lines and Angles

Fundamental Geometrical Concepts

Angles

Classification of Angles

Related Angles

Some Geometric Terms and Results

Complementary Angles

Supplementary Angles

Complementary and Supplementary Angles

Adjacent Angles

Linear Pair of Angles

Vertically Opposite Angles

Parallel Lines

Transversal Line

Parallel and Transversal Lines

7th Grade Math Problems 

8th Grade Math Practice 

From Complementary and Supplementary Angles to HOME PAGE