Subscribe to our YouTube channel for the latest videos, updates, and tips.
Classification of Angles
Angles can be classified according to their degree measures.
i.e, classification of angles on the basis of their degree measures are given below:
Acute Angle:
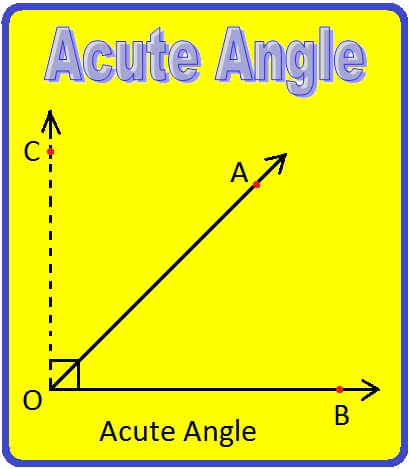
An angle whose measure is more than 0° but less than 90° is called an acute angle.
Definition of Acute Angle:
An angle measuring less than 90" is called an acute angle.
Angles having magnitudes 30°, 40°, 60° are all acute angles.
Examples of Acute Angle:
(i) Angles between two adjacent edges of scissors, etc.
(ii) Sun-rays make acute angle with the ground in the morning.
Right Angle:
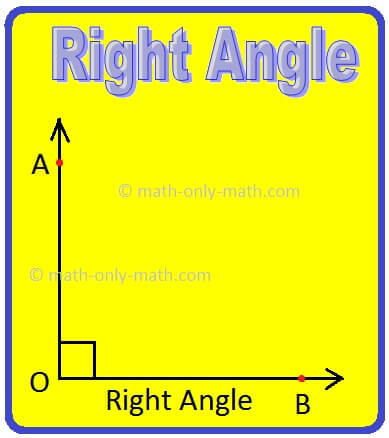
An angle whose measure is equal to 90° is called a right angle.
Definition of Right Angle:
An angle measuring 90° is called a right angle.
The arms of a right angle are perpendicular to each other.
In figure below, ∠AOB is a right angle.
Examples of Right Angle:
Corner of a room and Pillar on a ground form right angles.
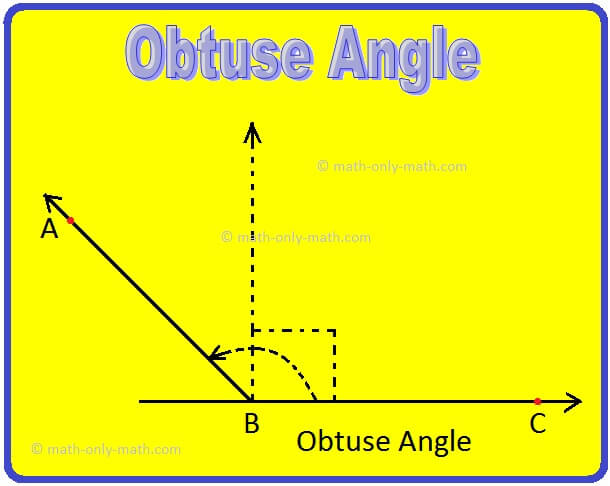
Obtuse Angle:
An angle whose measure is more than 90° but less than 180° is called an obtuse angle.
Definition of Obtuse Angle:
An angle greater than a right angle but less than two right angles is called an obtuse angle.
Its measure is more than 90° but less than 180°.
Examples of Right Angle:
Two adjacent sides of a microphone set, two edges of a book reading desk and two edges of the roof of a house form obtuse angles.
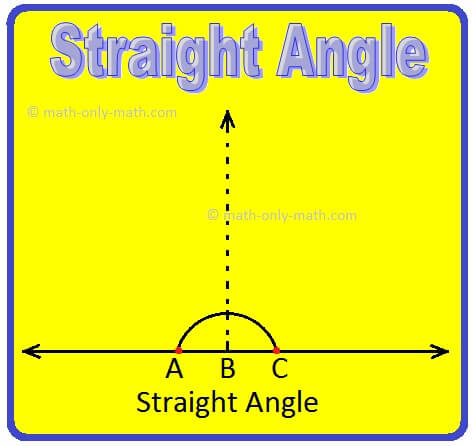
Straight Angle:
An angle whose measure is equal to 180° is called a straight angle.
Definition of Straight Angle:
An angle whose measure is 180° is called a straight angle.
Examples of Straight Angle:
Tubelight, pencil, a line segment form straight angles.
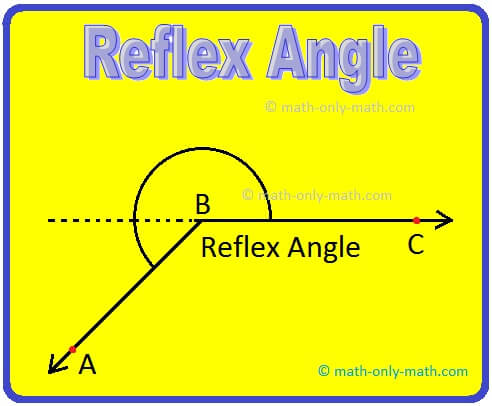
Reflex Angle:
A reflex angle is an angle which is larger than a straight angle. Its measure is more than 180º, but less than 360°.
Definition of Reflex Angle:
An angle whose measure is more than 180° but less than 360° is called a reflex angle.
Angles having magnitudes 220°, 250°, 310° are all reflex angles.
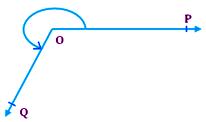
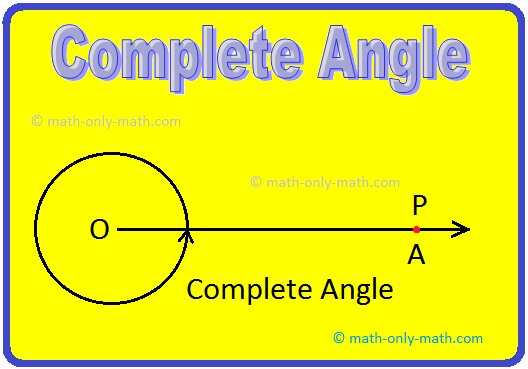
Complete Angle:
A complete angle is formed when the revolving ray OP (say) has made one complete revolution around the fixed point O after starting from the fixed initial position OA. The measure of a complete angle is 360°.
Definition of Complete Angle:
An angle whose measure is equal to 360° is called a complete angle.
Examples of Complete Angle:
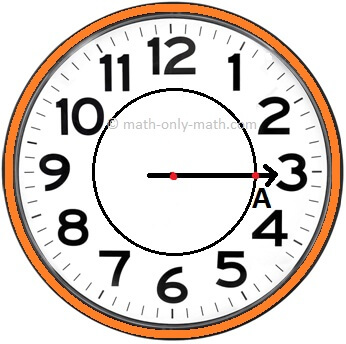
If the minute hand of a clock starts from point A (say) and returns back to this point after one complete revolution, then a complete angle of 360° is formed.
60 minutes = 1 revolution = 1 complete angle.
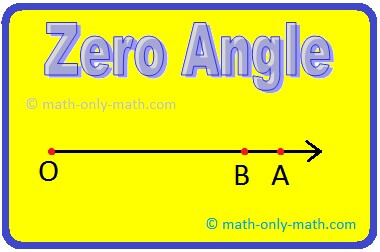
Zero Angle:
Definition of Zero Angle:
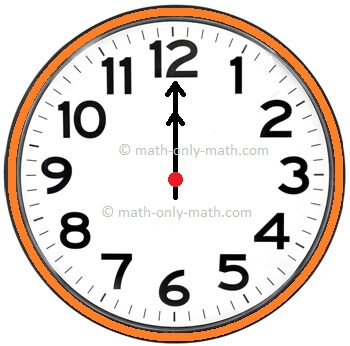
An angle of measure 0° is called a zero angle.
Example of Zero Angle:
The two hands of a clock in the 12 O' clock position before the start of any movement form zero angle.
The above explanation will help us to understand the classification of angles on the basis of their degree measures.
REMEMBER:
The magnitude of an angle does not depend upon the length of its arms.
Worksheet on Classification of Angles:
1. Multiple Choice Questions (MCQ) on Classification of Angles:
Tick (✔) the correct option.
(i) Which of the following angles is acute?
(a) 45°; (b) 180°; (c) 135°; (d) 90°
(ii) Which of the following is reflex angle?
(a) 195°; (b) 25°; (c) 135°; (d) 180°
Answer:
1. (i) (a) 45°
(ii) (a) 195°
2. What is the magnitude of the complete angle?
Answer:
2. 360°
3. State the angle whose magnitude is 0°.
Answer:
3. Zero angle
You might like these
Different Types of Polygons | Triangle, Quadrilateral|Pentagon|Hexagon
The different types of polygons are discussed here. In any polygon a pair of sides that are inclined to each other meet at a point. This point is called a vertex of the polygon. In the polygon there
Line Symmetry | Vertical & Horizontal Lines of Symmetry | Symmetrical
Line symmetry is discussed here. We know that any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical and the line which divides the shape in two equal halves is called the line of symmetry.
Simple Closed Curves | Types of Closed Curves | Collection of Curves
In simple closed curves the shapes are closed by line-segments or by a curved line. Triangle, quadrilateral, circle, etc., are examples of closed curves.
What is a Quadrilateral? | Symbol of a Quadrilateral □ | Rectangle
What is a quadrilateral? A simple closed curve or a polygon formed by four line-segments is called a quadrilateral.
Worksheet on Line Symmetry | Geometry Worksheet | Line of Symmetry
Worksheet on line symmetry we will solve different types of questions. 4th grade students can practice this geometry worksheet to get the basic ideas on line symmetry. Fill in the blanks: (i) A square has …... lines of symmetry. (ii) An equilateral triangle has
What is a Triangle? | Types of Triangle | Scalene Triangle | Isosceles
A simple closed curve or a polygon formed by three line-segments (sides) is called a triangle. The above shown shapes are triangles. The symbol of a triangle is ∆. A triangle is a polygon with three sides. In the given figure ABC is a triangle. AB, BC and CA are its sides.
Circle Math | Parts of a Circle | Terms Related to the Circle | Symbol
In circle math the terms related to the circle are discussed here. A circle is such a closed curve whose every point is equidistant from a fixed point called its centre. The symbol of circle is O. We have learned to draw a circle, by tracing the outlines of objects like a
What is a Polygon? | Simple Closed Curve | Triangle | Quadrilateral
What is a polygon? A simple closed curve made of three or more line-segments is called a polygon. A polygon has at least three line-segments.
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line which divides the shape is called the symmetry. So, if we place a mirror
Measuring the Line Segment | Comparing Line Segments
We will discuss here about measuring the line segment i.e. how to draw and measure a line segment using scale or ruler. We can measure a line segment by two ways. (i) With the help of scale
Comparing Different Line Segments | Difference of two line segments
We will discuss here about comparing different line segments. Different line segments can be of different lengths. We can compare the lengths of the different line segments
Constructing a Line Segment |Construction of Line Segment|Constructing
We will discuss here about constructing a line segment. We know how to draw a line segment of a certain length. Suppose we want to draw a line segment of 4.5 cm length.
Measuring an Angle | Using Protractor | Comparison of Angles | Example
We will discuss here about measuring an angle with the help of a protractor. You can find it in your Geometry Box. It has the semi-circular shape. Its semi-circular edge is divided
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of lengths of its three sides. The perimeter of a triangle ABC Perimeter
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opposite sides of a rectangle are equal. AB = CD = 5 cm and BC = AD = 3 cm
● Lines and Angles
Fundamental Geometrical Concepts
Some Geometric Terms and Results
Complementary and Supplementary Angles
Parallel and Transversal Lines
8th Grade Math Practice
From Classification of Angles to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Average Word Problems | Worksheet on Average Questions with Answers
May 20, 25 05:40 PM
In average word problems we will solve different types of problems on basic concept of average. 1. Richard scored 80, 53, 19, 77, 29 and 96 runs in 6 innings in a series. Find the average runs scored… -
Worksheet on Average | Word Problem on Average | Questions on Average
May 19, 25 02:53 PM
In worksheet on average we will solve different types of questions on the concept of average, calculating the average of the given quantities and application of average in different problems. -
8 Times Table | Multiplication Table of 8 | Read Eight Times Table
May 18, 25 04:33 PM
In 8 times table we will memorize the multiplication table. Printable multiplication table is also available for the homeschoolers. 8 × 0 = 0 8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 -
How to Find the Average in Math? | What Does Average Mean? |Definition
May 17, 25 04:04 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Problems Based on Average | Word Problems |Calculating Arithmetic Mean
May 17, 25 03:47 PM
Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.