Simple Closed Curves

In simple closed curves the shapes are closed by line-segments or by a curved line.

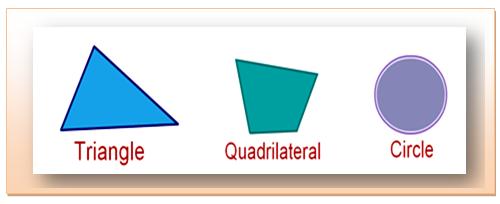
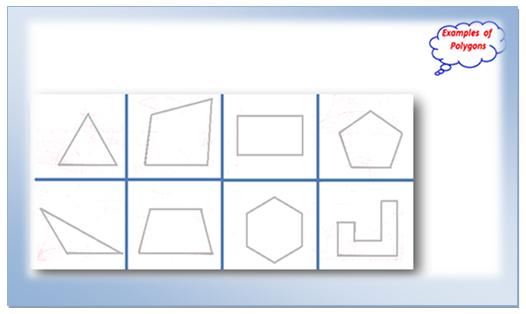
Triangle, quadrilateral, circle, etc., are examples of closed curves.

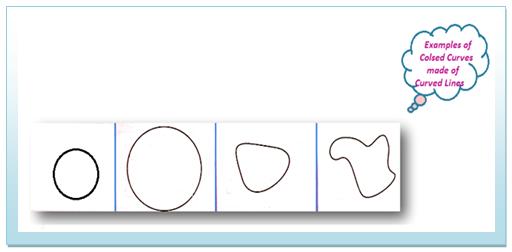
A curve which starts and ends at the same point without crossing itself is called a simple closed curve. A circle is a simple closed curve. 

Some more examples of simple closed curves are given below.

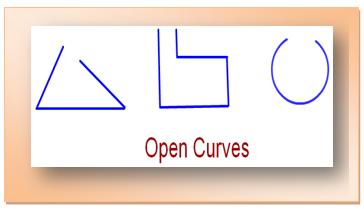
The shape which is not closed by line-segments or a curve is called an open curve.

The curves which do not have same starting and end points are called open curves.

Some examples of open curves are given below.

A closed curve which does not cross itself is called a simple open curve.

In the above figures, we can see the starting point and the end point are not the same Such figures are known as open curves.

The curve which crosses itself is not a simple closed curve.

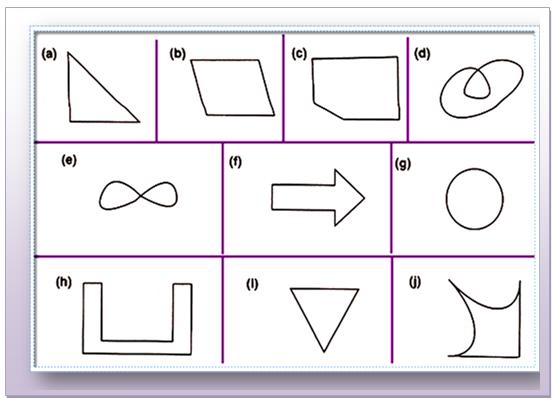
Here is a collection of closed curves. Except curve (d) and (e), the remaining shapes are simple closed curves.

There are three types of simple closed curves.

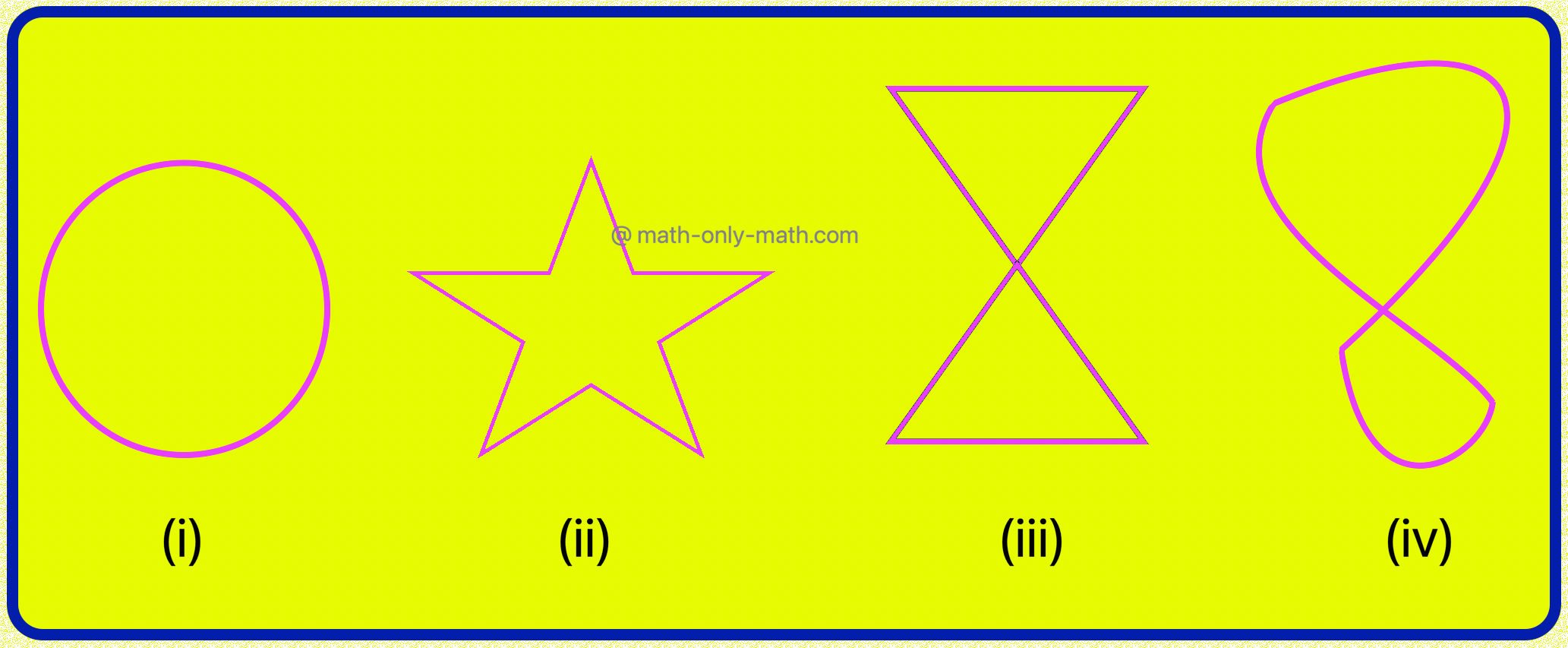
Observe the following curves:

In the above curves, (i) and (ii) are simple closed curves because they do not cross themselves as in the case of (iii) and (iv).

A closed curve which does not cross itself is called a simple closed curve.

Each of the following curves is a simple closed curve.

(i) Some simple closed curves are made of line-segments only. These curves are known as polygons. Triangle, quadrilateral, pentagon etc., are polygons.

The figures which have the same starting and the end-points are called closed curves.

(ii) Some simple closed curves are made by curved lines only. A circle is an example of such a closed curve.

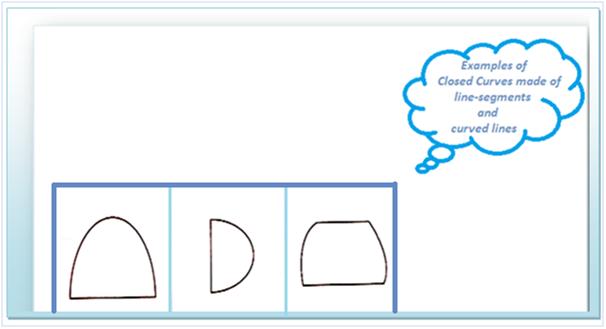
(iii) Some simple closed curves are made of both line-segments and curved lines.

Position in a Closed Curve:

In a closed curve, there are three disjointed parts:

(i) the interior or inside of the curve

(ii) boundary (on) of the curve

(iii) the exterior (outside) of the curve

In the given figure, A is the interior, B is the exterior and C is on the curve.

The interior of a curve together with its boundary is called its region.

Frequently asked questions:

1. What are a Curves?

Answer:

The pictures that are the results of doodling are called curves.

Generally, the word 'curve' cab be straight.

In mathematics, a curve can be straight.

2. What is Simple Curve?

Answer:

If a curve does not cross itself, it is called a simple curve.

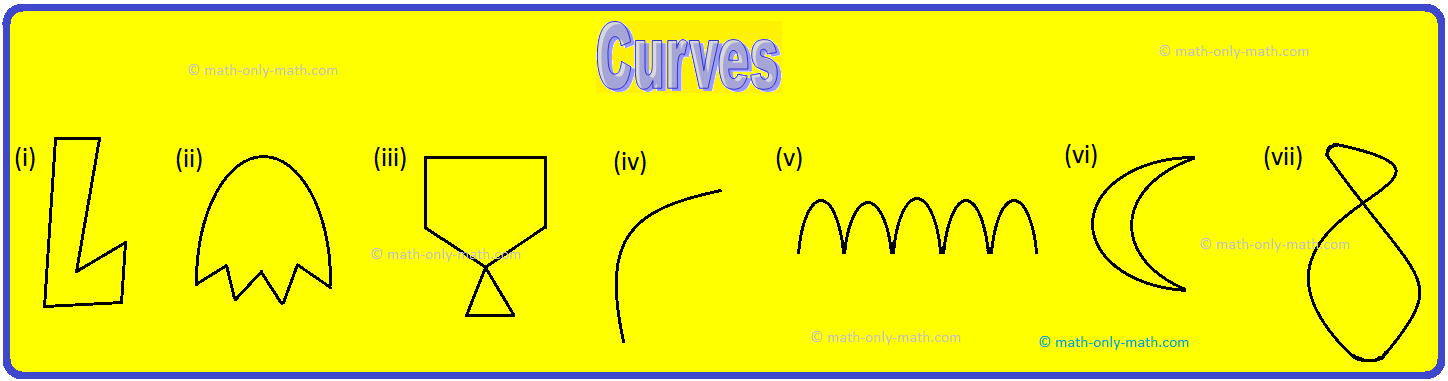
Observe that the curves (iii) and (vii) cross themselves, whereas the curves (i), (ii), (iv), (v) and (vi) do not cross.

The curves (i), (ii) (iv) (v) and (vi) do not cross themselves, hence are the examples of simple curves.

3. What are Open Curves?

The curves that do not begin and end at the same point are called open curves. The figures given below are the examples of the open curves.

4. What are Closed Curves?

The curves which begin and end at the same point are called closed curves.

The above figures are the examples of the closed curves.

Open and Closed Figures

Look at the following figures. All these shapes are made by lines in which a set of points change their direction. They have the same starting and end points. So, they are closed figures.

The figures given below have different starting and end points. So, they are called open figures.

Related Concepts on Geometry - Simple Shapes & Circle

● Simple Closed Curves

● Polygon

● Different Types of Polygons

● Angle

● Triangle

● Quadrilateral

● Circle Math

● Line Symmetry

● Symmetrical Shapes

4th Grade Math Worksheets

Math Homework Sheets

From Simple Closed Curves to HOME PAGE