Comparing Different Line Segments

We will discuss here about comparing different line segments.

A line segment is a part of a line. It has two end points and has a definite length, no breadth and no thickness. The length of a line segment is a distance that can be measured in metres, centimetres, millimetres etc.

10 mm (millimetres) = 1 cm (centimetre)

10 cm (centimetre) = 1 dm (decimetre)

10 dm (decimetres) = 1 m (metre)

10 m (metre) = 1 dam (decametre)

10 dam (decametres) = 1 hm (hectometre)

10 hm (hectometres) = 1 kilometre (km)

Comparing Two Line Segments:

Comparing two line segments implies establishing a relationship between their lengths whether one line segment is greater than or equal to or less than the other line segment. Comparison of line segment can be done in several ways.

(i) Comparison by Observation.

Line segments can be compared easily by observation by placing a line segment below another segment and judging the length visually.

Working Rules for Comparison of Two Line Segments by Observation:

Step I: Draw two line segments of different lengths.

Step II: Label them. Place one line segment below another line segment.

Step III: By observation compare the two line segments.

Example:

Compare the following two line segments by observation:

Solution:

\(\overline{PQ}\) is longer than \(\overline{AB}\) , as PQ extends farther to the right of \(\overline{AB}\).

(ii) Comparison by Tracing.

One cannot always be sure about visual judgement. By looking at the segment, the difference in length of two line segments may not be obvious. We require better methods of comparing line segments. One such method is comparison by tracing and superimposing.

Working Rules for Comparison of Two line Segments by Tracing:

Step I: Use a tracing paper to trace the line segment, say overline \(\overline{PQ}\).

Step II: Place the traced line segment \(\overline{PQ}\) the other line segment, say \(\overline{AB}\).

Step III: If \(\overline{PQ}\) on the tracing paper covers \(\overline{AB}\) behind it, then \(\overline{PQ}\) is longer than \(\overline{AB}\), otherwise \(\overline{AB}\) is longer than \(\overline{PQ}\).

Example:

Compare \(\overline{PQ}\) and \(\overline{AB}\) by tracing.

Solution:

To compare \(\overline{PQ}\) and \(\overline{AB}\), use a tracing paper. Trace \(\overline{AB}\) and place it on the line segment \(\overline{PQ}\). On tracing, it is known that \(\overline{PQ}\) is greater than \(\overline{AB}\).

(iii) Comparison Using a Divider.

Different line segments can be of different lengths. We can compare the lengths of the different line segments with the help of a divider.

In geometry-box, there is an instrument called divider. A divider has two arms hinged together. Each arm has a pointed metallic end. The distance between the two ends can be increased or decreased as required.

1. Let us now compare any two line segments, say \(\overline{PQ}\) and \(\overline{AB}\) using a divider.

Working Rules for Comparison of Two line Segments Using Divider:

Step I: Place the end-point of one arm of the divider at A.

Step II: Open the divider in such a way that the end-point of the other arm reaches at the other point B.

Step III: Lift the divider and without disturbing its opening, place the end-point of one arm at P.

Now, the three following cases may arise:

Case (i): The second arm of the divider falls on Q. In this case, we can say that lengths of the line segments AB and PQ are equal and write AB = PQ.

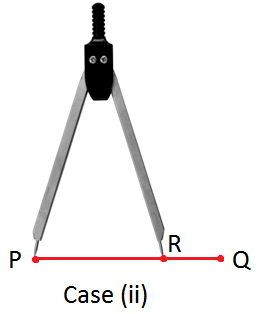
Case (ii): The second arm falls at a point R between P and Q. In this case, we conclude that the line segment AB is shorter than the line segment PQ and write AB < PQ.

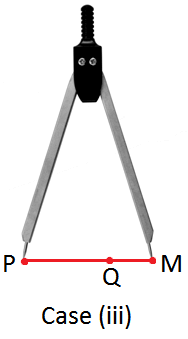
Case (iii): The second arm falls at a point M outside PQ. In this case, we conclude that the line segment AB is longer than the line segment PQ and write AB > PQ.

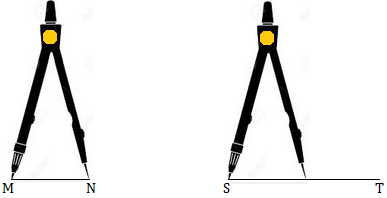
2. Let us compare two line segments MN and ST.

I. First, place one point of the divider on the end point M of the line segment MN. Now we open the pair of divider in such a way that the other point of divider falls on the other end point N.

II. Then we lift the divider very carefully so that its arms are not disturbed.

III. Now place one end point of the pair of divider on the end point S of the other line segment ST and let the other end point of the pair of divider rest on the line segment ST as shown in figure.

We see that this end point falls before the other end point T of the line segment ST. This shows that the line segment MN is shorter than the line segment ST. If the end point of the divider falls beyond the point T, MN is longer than ST.

Example:

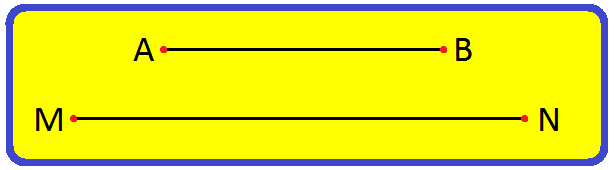
1. Compare the two line segments AB and MN using a divider.

Solution:

Place the end-point of one arm of the divider at A. Open the divider in such a way that the end-point of the other arm reaches at the other point B. Lift the divider and without disturbing its opening, place the end-point of one arm at M and the other at N.

On comparing, it is being noticed that AB < MN.

4th Grade Math Activities

From Comparing Different Line Segments to HOME PAGE