Quadrilateral

What is a quadrilateral?

A simple closed curve or a polygon formed by four line-segments or sides is called a quadrilateral.

The four line-segments forming a quadrilateral are called its sides.

For example - squares, rectangles, rhombuses, trapeziums and parallelograms are quadrilaterals.

A quadrilateral has four sides and four angles.

The symbol of a quadrilateral is □.

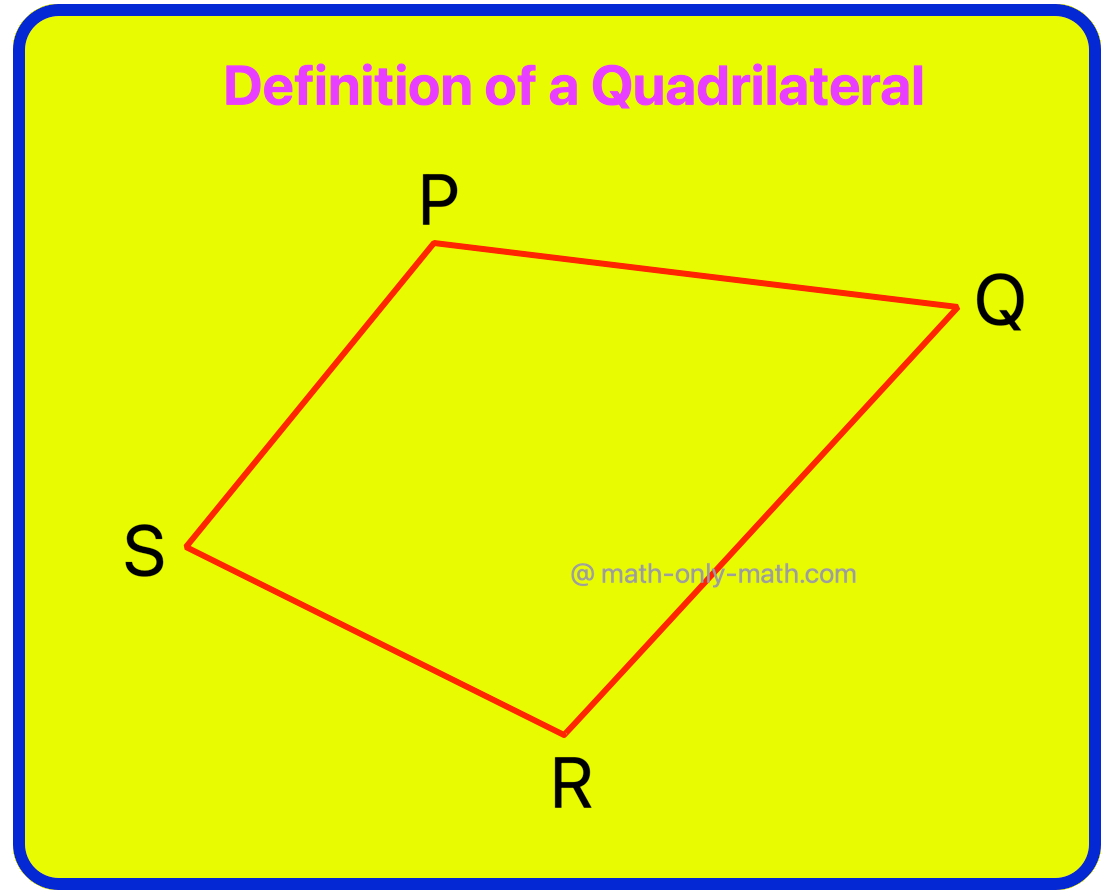
Definition of a Quadrilateral:

A closed figure bounded by four line segments on a plane is called quadrilateral.

If P, Q, R, S are four points in a plane such that no three of them are collinear and the line segments PQ, QR, RS and SP do not intersect except at their end-points, the figure formed by these four line segments is called a quadrilateral.

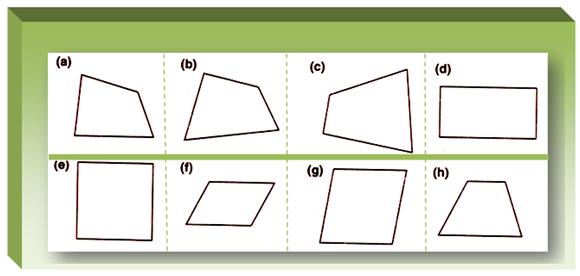
Each shape shown below is a quadrilateral.

(i) Shape (d) is a special type of quadrilateral. Its opposite sides are equal. Each angle of it is a right angle. Its name is rectangle.

AB = CD, AD = BC and ∠DAB = ∠ABC = ∠BCD = ∠CDA = 90°.

(ii) The quadrilateral (e) is named as square. All the sides of it are of equal measure and each angle is a right angle.

In the above figure, AB = BC = CD = DA and ∠ABC = ∠BCD = ∠DAB = ∠CDA = 90°.

(iii) Shape (f) is a quadrilateral having the special name parallelogram and with opposite sides equal and parallel.

It has also its opposite angles equal.

In the above figure, AB and CD are equal and parallel. Similarly, AD and BC are equal and parallel.

∠DAB = ∠DCB and ∠CDA = ∠CBA.

(iv) Shape (g) is the shape of a rhombus whose all sides are equal.

A rhombus is a parallelogram with all its sides equal.

Its two opposite angles are equal and greater than 90°. Its other two opposite angles are equal and less than 90°.

Note: A rhombus cannot have any right angle.

In the above figure, AB = BC = CD = DA. AB is parallel to CD and AD is parallel to BC.

∠DAB = ∠DCB and ∠CDA = ∠CBA

No angle is right angle.

(v) The quadrilateral (h) is the shape of a trapezium.

A trapezium is a quadrilateral which has a pair of opposite sides parallel.

In the above figure, opposite sides AB and CD are parallel.

A polygon covers a plane space whose area may be calculated. The length of the covering sides is called its perimeter.

Note: The sum of angles of a quadrilateral is always 360°.

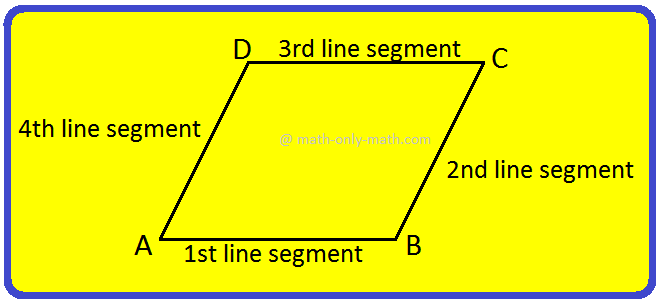
Working Rules to Form a Quadrilateral:

Step I: Take four line segments. Join two line segments end to end. By joining them one angle if formed.

Step II: Now, join the third line segment to the second line segment at its free end.

Step III: Fix the fourth line segment such that it joins the first and A third line segments.

Step IV: On joining the fourth line segment, it gives a particular shape.

Step V: We have taken four line segments and joined them in definite pattern to form four angles.

We call it a quadrilateral; quadri = four, lateral = sides

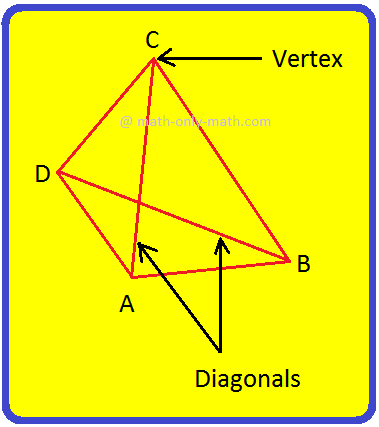
Sides, Angles and Diagonals of a Quadrilateral:

(i) The four line segments AB, BC, CD and DA are called its sides. (ii) The four angles ∠DAB, ∠ABC, ∠BCD and ∠CDA are called its angles. (iii) A line segment joining two non-consecutive (opposite) vertices is called a diagonal.

AC and BD are the two diagonals of the quadrilateral ABCD.

Adjacent Sides and Opposite Sides of a Quadrilateral:

Adjacent Sides of a Quadrilateral: Two sides of a quadrilateral are said to be adjacent sides, if they have a common end point.

Opposite Sides of a Quadrilateral: Two sides of a quadrilateral are said to be opposite sides, if they are not adjacent sides.

Thus, in the quadrilateral ABCD shown above, (AB, AD) is a pair of adjacent sides. So also are the pairs of sides (AB, BC) and (BC, CD). Again, in the same figure, (AB, DC) is a pair of opposite sides and (BC, AD) is the other pair of opposite sides.

Adjacent Angles and Opposite Angles of a Quadrilateral:

Adjacent Angles of a Quadrilateral: Two angles of a quadrilateral are said to be adjacent angles, if they have a common side.

Opposite Angles of a Quadrilateral: Two angles of a quadrilateral are said to be opposite angles, if they are not adjacent angles.

Thus, in the above figure, (∠A, ∠B) is a pair of adjacent angles of the quadrilateral ABCD, as they have common side AB.

Similarly, (∠B, ∠C); (∠C, ∠D); and (∠D, ∠A) are the other pairs of adjacent angles.

Again, in the same figure, (∠A, ∠C) is a pair of opposite angles; so also is the pair of angles (∠B, ∠D).

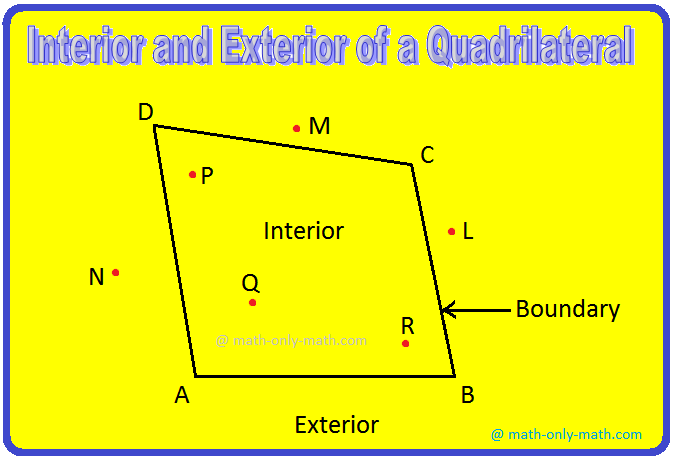
Interior and Exterior of a Quadrilateral:

Look at the above figure.

Do you observe that the quadrilateral ABCD divides all the points in the plane into three parts?

(i) The part of the plane which consists of the points P, Q, R lies inside the quadrilateral. This part is called the interior of the quadrilateral. The points P, Q, R lies inside the quadrilateral. The point P, Q, R are called the interior points of the quadrilateral.

(ii) The part of the plane which consists of the points L, M, N lies outside the quadrilateral. This part is called the exterior of the quadrilateral. The points like L, M, N are called exterior points of the quadrilateral.

(iii) The quadrilateral itself consists of its sides. It is the boundary of its interior.

Quadrilateral Region:

The interior of the quadrilateral ABCD together with the quadrilateral itself is called the quadrilateral region.

Math Questions and Answers on Quadrilaterals:

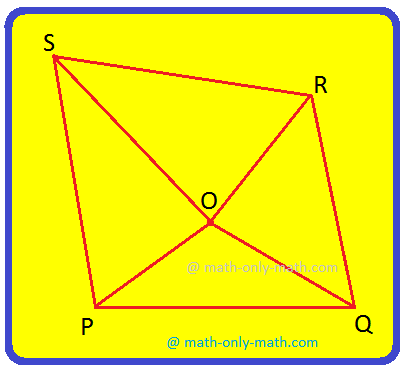
1. Take a point O inside a given quadrilateral PQRS. Join the point O to the vertices P, Q, R and S. In what figures will the quadrilateral be divided into? Name the figures.

Solution:

Quadrilateral PQRS is divided into four triangles i.e., ΔΡΟS, ΔROS, ΔPOQ and ΔQOR.

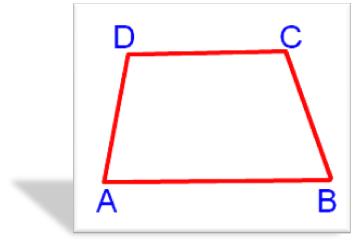
2. In the figure, ABCD is a quadrilateral.

(i) How many pairs of adjacent sides are there? Name them.

(ii) How many pairs of opposite sides are there? Name them.

(iii) How many pairs of adjacent angles are there? Name them.

(iv) How many pairs of opposite angles are there? Name them.

Solution:

(i) There are four pairs of adjacent sides i.e., (AB, BC); (BC, CD); (CD, DA); (DA, AB).

(ii) There are 2 pairs of opposite sides i.e., (AB, CD); (AD, BC).

(iii) There are four pairs of adjacent angles i.e., (∠A, ∠D); (∠D, ∠C); (∠C, ∠B); (∠B, ∠A).

(iv) There are 2 pairs of opposite angles i.e., (∠A, ∠C) and (∠B, ∠D).

Related Concepts on Geometry - Simple Shapes & Circle

● Simple Closed Curves

● Polygon

● Different Types of Polygons

● Angle

● Triangle

● Quadrilateral

● Circle Math

● Line Symmetry

● Symmetrical Shapes

4th Grade Math Activities

From Quadrilateral to HOME PAGE