Circle Math

In circle math the terms related to the circle are discussed here.

A circle is a closed figure that has a curvilinear boundary. A circle is a simple closed curve, all the points of which are at the same distance from a given interior fixed point. They remain constant.

For Example: Wheels of a car, bus, cycle, truck, the sun, the moon, one rupee coin, etc.

We have learned to draw a circle, by tracing or moving a pencil around the outlines of objects like a bangle or a bottle cap.

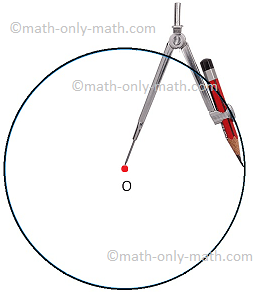
We shall learn now how to draw a circle using a compass.

Compass is a handy drawing tool available in the geometry box. A compass has two arms which can be pulled apart easily to adjust to the size of the circle we want to draw.

Fix a sharp pencil into the holder on the compass.

Fix the needle of the compass on the point where the center of the circle would be.

Open and adjust the other arm which is holding the pencil and rotate the compass to draw a circle.

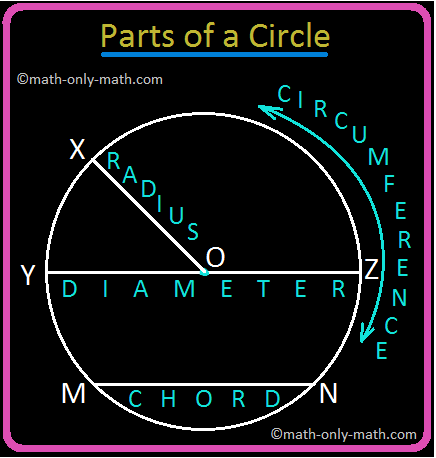
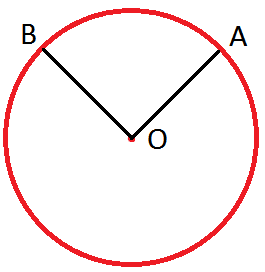
The point O where the needle of the compass is placed in the centre of the circle. The distance of any point on the circle from the centre O is the radius of the circle. In the given figure OX is the radius.

A line segment which joins any two points on the circle is called a chord. MN is a chord in the given figure.

The line passing through the centre which joins two points on the circle is the diameter. Diameter of the circle is twice its radius. YZ is the diameter of the circle in the given figure.

The length of the circle is called its circumference.

A circle is such a closed curve whose every point is equidistant from a fixed point called its center.

The symbol of circle is O.

Parts of a Circle:

What are the terms related to the circle?

The terms related to the circle math are:

(i) Center:

The center of a circle is a fixed point within the circle from which all the points of the closing curve are equidistant. 

Definition of Center of a Circle:

The fixed point in the plane which is equidistant from every point on the boundary of a circle is called centre. In the figure below, O is the centre of the circle.

The point O inside the circle is the center of the circle.

(ii) Circumference:

The curve which closes a circle is called its circumference. The length of the circumference is called the length of the circle.

Definition of Circumference of a Circle: The boundary around a circle is called the circumference.

Circumference of a circle is the perimeter of that circle.

The length of a circle (distance around) is called the circumference of the circle.

(iii) Radius:

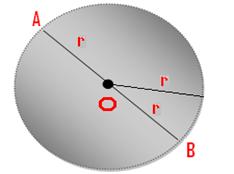
The distance from the centre to any point on the circumference of a circle is called the radius of the circle. The symbol of the radius is r.

Definition of Radius of a Circle:

The fixed distance between the centre and any point boundary of on the boundary of a circle is called radius. 

A line segment drawn from the center to any point on the circle is called a radius of the circle. In the figure, the line segment OA is a radius of the circle. Line segment OB is also a radius of the circle.

(iv) Diameter:

A chord that passes through the centre of a circle is called diameter of the circle. In the figure below, AB is a diameter.

Length of a diameter = 2 x radius.

In a circle, diameter is the longest chord.

Definition of Diameter of a Circle:

The line-segment passing through the centre and meeting the points on the circumference is called the diameter of the circle. Diameter is denoted by 'D'.

The line segment drawn through the center that joins two points on the circle is called a diameter of the circle. In the figure above, line segment AB is a diameter of the circle.

AB is a diameter of the circle.

Diameter is twice the length of the radius concerned.

Thus, D = 2r [Diameter = 2 radius]

or

r = D/2 [Radius = Diameter/2]

(v) Arc:

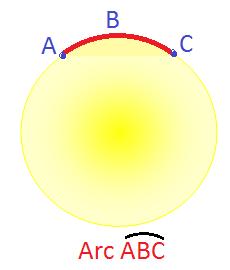
Any part of the circumference is called an arc of the circle.

Definition of an Arc of a Circle:

A part of a circumference of a circle is called an arc.

In the above figure, the curve line ABC is an arc of the circle.

It is written as

(vi) Chord:

The line-segment joining the two ends of an arc is known as a chord. A diameter is the longest chord of a circle.

or,

Definition of Chord of a Circle:

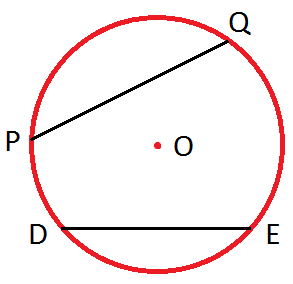
A line segment joining any two points on the boundary of on the boundary circle is called a chord of the circle.

A line segment that joins two points on a circle is called a chord of the circle. In the figure, line segment PQ and DE are chords of the circle.

REMEMBER: Diameter id the longest chord of a circle.

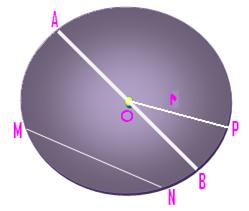
Now observe the figure below:

Here,

O is the centre.

OP is one radius.

AB is a diameter.

MN is a chord. (line-segment)

OA and OB are also radii.

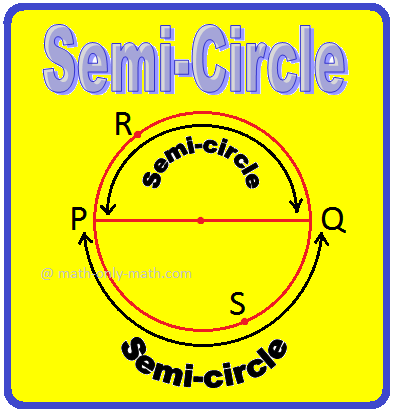
(vii) Semi-Circle:

The end-points of a diameter of a circle divide the circle into two equal parts; each part is called a semi-circle.

In the above figure, PRQ and PSQ are semi-circles.

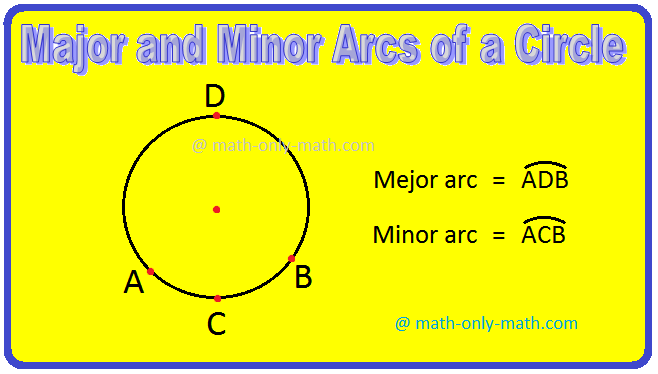
(viii) Major and Minor Arcs of a Circle:

Major Arc: If the arc of a circle is greater than the half or the circumference of a circle, it is called a major arc.

Minor Arc: If the arc of a circle is less than the half or the circumference of a circle, it is called a minor arc.

In the above figure, ADB is the major arc and ACB is the minor arc.

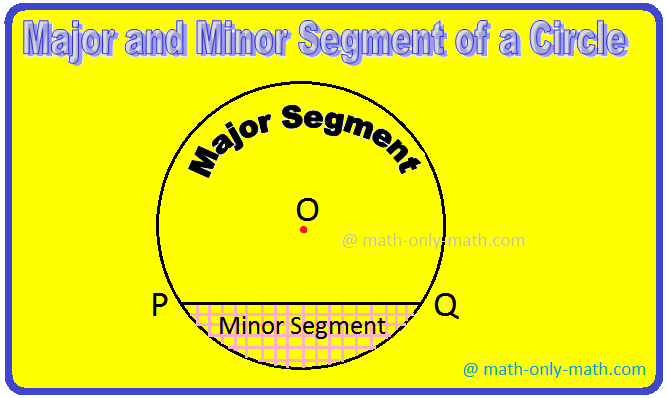
(ix) Segment of a Circle:

When a chord of a circle divides the circular region into two parts, each part is called a segment of the circle.

Major and Minor Segment of a Circle: The segment containing the centre of the circle is called the major segment, while the segment not containing the centre is called the minor segment of the circle.

In the above figure, the unshaded region is the major segment and shaded region is the minor segment of the circle.

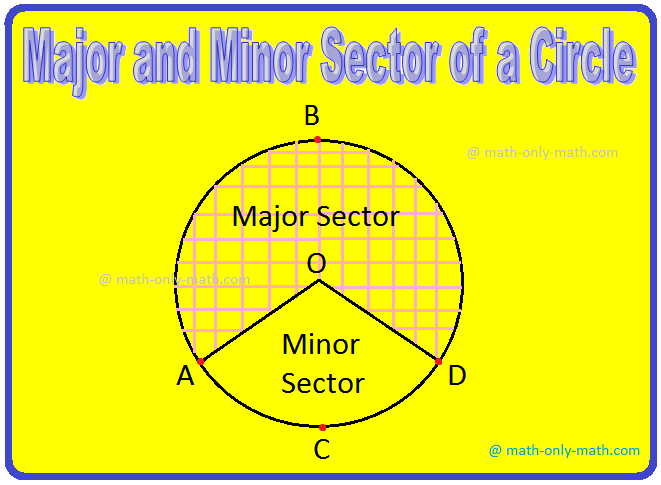
(x) Sector of a Circle:

The area bounded by an arc and two radii joining the centre to the end points of the arc is called a sector of the circle.

Major and Minor Sector of a Circle: 

The sector formed by a major arc is called major sector and the sector formed by a minor arc is called minor sector.

In the above figure, OABD (shaded region) is the major sector and OACD (unshaded region) is the minor sector of the circle with centre O.

Drawing a Circle:

We can also draw a circle using a pair of compasses. To do so, we proceed as follows:

Step I: Fix a sharpened pencil in the compass. Step II: Open the compasses to any suitable length. Step III: Make a point on a piece of paper. Step IV: Put the metal end of the compasses at the point O Step V: Let the pencil-point touch the paper. Step VI: Move the pencil around, keeping the metal point fixed at the point O. Remove the compasses. The figure you get is a circle.

Circle Math Questions and Answers:

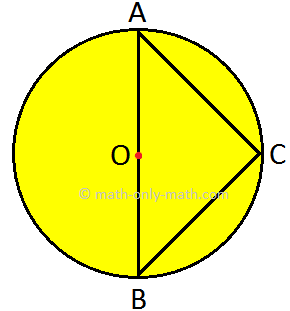
1. In the given circle, find the following: (i) three radii (ii) three chords (iii) a diameter (iv) a triangle that has the centre of the circle as vertex.

Solution:

(i) Three radii: \(\overline{OA}\), \(\overline{OB}\) and \(\overline{OC}\).

(ii) Three chords: \(\overline{AC}\), \(\overline{BC}\) and \(\overline{AB}\)

(iii) Diameter: \(\overline{AB}\)

(iv) A triangle that has the centre of the circle as vertex is ∆AOC or ∆BOC

2. The diameter of the circle of radius 7 cm is __________. 

Solution:

Diameter = 2 × radius = 2 × 7 cm = 14 cm.

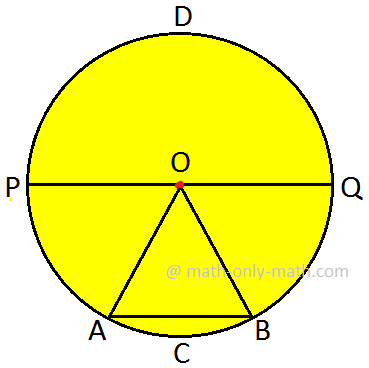
3. In the following circle, name: (i) major segment. (ii) minor arc. (iii) major sector (iv) semi-circle.

Solution:

(i) APDQB

(ii) arc ACB

(iii) OAPDQB

(iv) PCQ and PDQ are two semi-circles.

Worksheet on Circle Math:

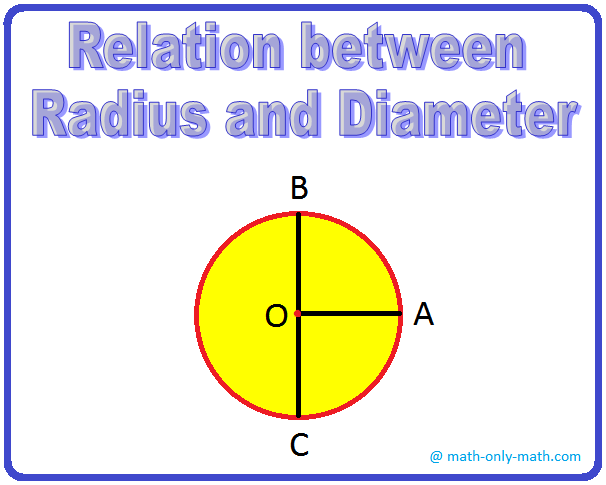
1. Look at the adjoining figure of a circle. Measure its radius OA and diameter BC. Find the relation between radius and diameter.

OA = __________ cm BC = __________ cm BC = __________ OA

2. Complete the following table regarding circles:

Answer:

2. 

Related Concepts on Geometry - Simple Shapes & Circle

● Simple Closed Curves

● Polygon

● Different Types of Polygons

● Angle

● Triangle

● Quadrilateral

● Circle Math

● Line Symmetry

● Symmetrical Shapes

4th Grade Math Activities

From Circle Math to HOME PAGE