Vertically Opposite Angles



What is vertically opposite angles?

When two straight lines intersect each other four angles are formed.



The pair of angles which lie on the opposite sides of the point of intersection are called vertically opposite angles.

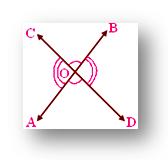
In the given figure, two straight lines AB and CD intersect each other at point O. Angles AOD and BOC form one pair of vertically opposite angles; whereas angles AOC and BOD form another pair of vertically opposite angles.

vertically opposite angles diagram, vertically opposite angles



Vertically opposite angles are always equal.
i.e., ∠AOD = ∠BOC
and ∠AOC = ∠BOD


Note:

opposite angles, vertically opposite angles



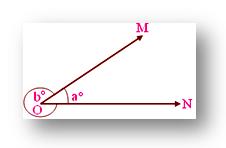
In the given figure; rays OM and ON meet at O to form ∠MON (i.e. ∠a) and reflex ∠MON (i.e. ∠b). It must be noted that ∠MON means the smaller angle only unless it is mentioned to take otherwise.


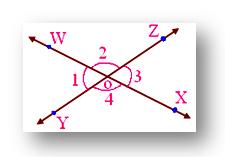
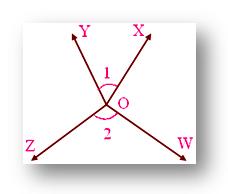
For example; in the given figure, two lines WX and YZ are intersecting at a point O.

vertically opposite angles image, vertically opposite angles



We observe that with the intersection of these lines, four angles have been formed. Angles ∠1 and ∠3 form a pair of vertically opposite angles; while angles ∠2 and ∠4 form another pair of vertically opposite angles.

Clearly, angles ∠1 and ∠2 form a linear pair.
Therefore, ∠1 + ∠2 = 180°
or, ∠1 = 180° - ∠2 …………(i)

again similarly, ∠2 and ∠3 form a linear pair.
Therefore, ∠2 + ∠3 = 180°
or, ∠3 = 180° - ∠2 …………(ii)

From (i) and (ii) we get;
∠1 = ∠3
Similarly, we can prove that ∠2 = ∠4
Thus, if two lines intersect then vertically opposite angles are always equal.

In the below figure, ∠1 and ∠2 are not vertically opposite angles, because their arms do not form two pairs of opposite rays.

vertically opposite angles picture, vertically opposite angles



Now, we will solve various examples on vertically opposite angles.



Worked-out problems on vertically opposite angles:

1. In the given figure, find the measure of unknown angles.

vertically opposite angles problems, vertically opposite angles



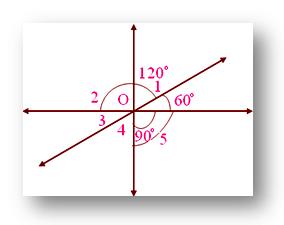
Solution:

(i) ∠3= 60° vertically opposite angles

(ii) ∠2 = 90° vertically opposite angles

(iii) ∠2 + ∠1 + 60° = 180° (straight angle)
90° + ∠ 1 + 60° = 180°
150° + ∠ 1 = 180°
Therefore, ∠1 = 180° — 150° = 30°

(iv) ∠1 = ∠4 vertically opposite angles
Therefore, ∠4 = 30°


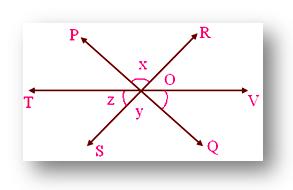
2. In the given figure, lines PQ, RS, TV intersect at O. If x : y : z = 1 : 2 : 3, then find the values of x, y, z.

problems on vertically opposite angles, vertically opposite angles



Solution:

The sum of all the angles at a point is 360°.

∠POR = ∠SOQ = x° (Pair of vertically opposite angles are equal.)

∠VOQ = ∠POT = y° (Pair of vertically opposite angles are equal.)

∠TOS = ∠ROV = z° (Pair of vertically opposite angles are equal.)

Therefore, ∠POT + ∠POR + ∠ROV + ∠VOQ + ∠QOS + ∠SOT = 360°

y + x + z + y + x + z = 360°
⟹ 2x + 2y + 2z = 360°
⟹ 2(x + y + z) = 360°
⟹ x + y + z = 360°/2
⟹ x + y + z = 180° --------- (i)

Let the common ratio be a.
Therefore, x = a, y = 2a, z = 3a

Therefore, from the equation (i) we get;
a + 2a + 3a = 180°
⟹ 6a = 180°
⟹ a = 180°/6
⟹ a = 30°

Therefore, x = a, means x = 30°
y = 2a, means y = 2 × 30 = 60°
z = 3a, means z = 3 × 30 = 90°
Therefore, the measures of the angles are 30°, 60°, 90°.



● Lines and Angles

  • Fundamental Geometrical Concepts
  • Basic Geometrical Concepts
  • Angles
  • Classification of Angles
  • Related Angles
  • Some Geometric Terms and Results
  • Complementary Angles
  • Supplementary Angles
  • Complementary and Supplementary Angles
  • Adjacent Angles
  • Linear Pair of Angles
  • Vertically Opposite Angles
  • Parallel Lines
  • Transversal Line
  • Parallel and Transversal Lines

    • 7th Grade Math Problems

    8th Grade Math Practice

    From Vertically Opposite Angles to HOME PAGE

    © and ™ math-only-math.com. All Rights Reserved. 2010 - 2012.