Worksheet on Volume
In worksheet on volume we will solve 10 different types of question in volume.
1. The amount of space occupied by a solid is ………..
2. Find the volume of a cube of side 14 cm.
3. Find the volume of a cube of side 17 mm.
4. Find the volume of a cube of side 27 m.
5. Find the volume of a cuboid of dimension 18 cm × 120 mm × 150 mm in cu. cm.
6. Find the volume of a cuboid of dimensions 15 cm × 12 cm × 3 cm.
7. How many cubes of 5 cm are equivalent in volume to a 15 cm cube?
8. Find the volume of a cuboid of dimensions 12 m × 14 m × 3.5 m.
9. How many more cubes are required in Object ’A’ to make the volume equal to Object ‘B’?
10. Find the volume of a cuboid of dimensions 89 mm × 71 mm × 60.5 mm.
11. Find the volume of oil that can be poured into a container of dimensions 13 cm × 8 cm × 11 cm.
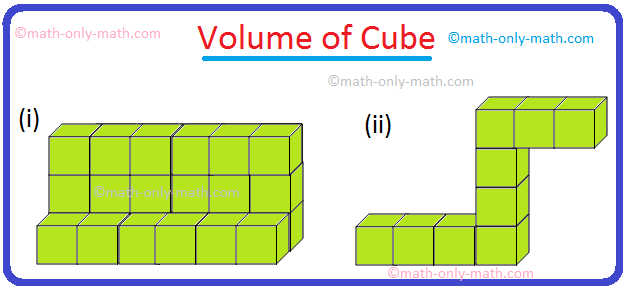
12. Find the volume of the given figures. Take the volume of each small cube as 1 cu cm.
13. A cubical of wood was cut into 8 equal cubes of sides 4 cm. What is the volume of the block of wood?
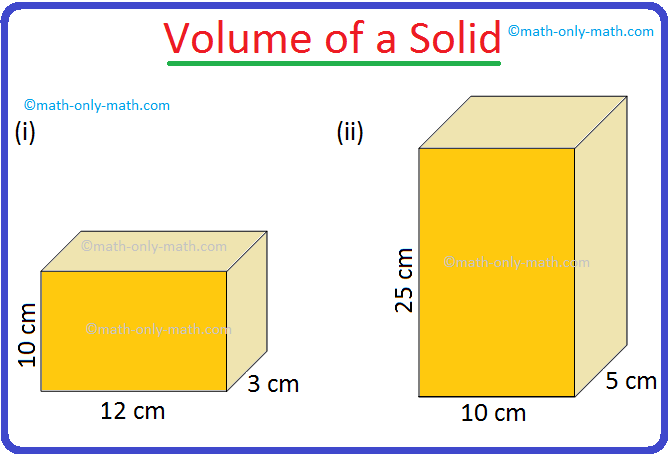
14. Find the volume of the given solid.
15. Find the volume of a cuboid of dimensions 8500 cm × 950 mm × 15 m.
Answers:
1. Volume
2. 2744 cu. cm.
3. 4913 cu. mm.
4. 19683 cu.m.
5. 3240 cu. cm.
6. 540 cu. cm.
7. 27
8. 588 cu. m.
9. 36 cubes
10. 382299.5 cu. mm.
11. 1144 cu. cm.
12. (i) 24 cu cm
(ii) 9 cu cm
13. 512 cu. m.
14. (i) 360 cu cm
(ii) 1250 cu cm
15. 1211.25 cu. m.
● Volume.
Worksheet on Volume of a Cube and Cuboid
5th Grade Math Problems
5th Grade Math Worksheets
From Worksheet on Volume to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on 10 Times Table | Printable Multiplication Table | Video
Mar 21, 25 03:46 PM
Worksheet on 10 times table can be printed out. Homeschoolers can also use these multiplication table sheets to practice at home. -
5th Grade Prime and Composite Numbers | Definitions | Examples | Math
Mar 21, 25 12:18 AM
5th grade prime and composite numbers -
14 Times Table | Read and Write Multiplication Table of 14| Video
Mar 20, 25 04:03 PM
In 14 times table we will learn how to read and write multiplication table of 14. We read fourteen times table as:One time fourteen is 14 Two times fourteen are 28 Three times fourteen are 42 -
5th Grade Test of Divisibility Rules | Divisibility Rules From 2 to 12
Mar 20, 25 04:00 PM
In 5th grade test of divisibility rules we will learn about the exact divisibility of a number by the numbers from 2 to 12. The digit in the ones place should be 2, 4, 6, 8 or 0. -
5th Grade Even and Odd Numbers | Definitions | Examples
Mar 20, 25 02:45 AM
Numbers which are exactly divisible by 2 are even numbers. For example. 2,4,6,8,20,48,88, etc. are even numbers. They are multiples of 2. Numbers which are not exactly divisible by 2 are odd numbers…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.