Subscribe to our YouTube channel for the latest videos, updates, and tips.
Division of Four-Digit by a One-Digit Numbers
In division of four-digit by a one-digit numbers are discussed here step by step.
How to divide 4-digit numbers by single-digit numbers?
Let us follow the examples to learn to divide 4-digit numbers by one-digit numbers.
Divide and find the quotient:
(i) 3408 ÷ 3
(ii) 6585 ÷ 5
(iii) 4107 ÷ 6
(iv) 7608 ÷ 8
Solution:
The same procedure will be adopted to divide a 4-digit number by a single digit number.
(i) 3408 ÷ 3
3 x 1Th = 3Th, 1Th is the quotient
3 x 1H = 3H, 3 x 2H = 6H, 1H is the quotient
3 × 3T = 9T, 3 x 4T = 12T, 3T is the quotient
3 × 6 = 18, 6 is the quotient
Verification
3 × 1136 + 0 = 3408 + 0 = 3408
So, result is verified.
Quotient = 1136
or,
Instead of 3000, we put 3
Instead of 300, we put 3
Instead of 90 we put 9
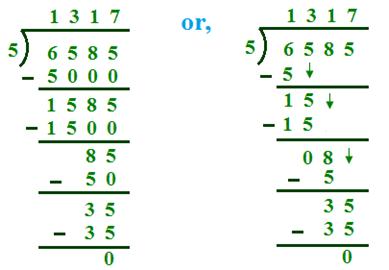
(ii) 6585 ÷ 5
(i) 5 × 1Th = 5Th. 1Th is quotient
6Th - 5Th = 1Th
(ii) 5 × 3H = 15H, 3 H is quotient
(iii) 5 × 1T = 5T, 1T is quotient
(iv) 8T - 5T = 3T, 5 is carried down
5 × 7 = 35, 7 will be quotient
Quotient = 1317
Verification = 5 × 1317 + 0 = 6585 + 0 = 6585.
Result is verified.
(iii) 4107 ÷ 6
Quotient = 684 Remainder = 3
(i) 4 < 6, So, 41 is taken for division
6 × 6 = 36, 6 × 7 = 42,
6H will be quotient.
(ii) 50 is taken for division
6 × 8 = 48, 6 x 9 = 54,
8T is the quotient.
(iii) 27 is taken for division
6 × 4 = 24, 6 × 5 = 30
Therefore, 4 is the quotient.
Verification = 6 × 684 + 3 = 4104 + 3 = 4107.
So, result is verified.
(iv) 7608 ÷ 8
Quotient = 951 Remainder = 0
(i) 7 < 8, So 76 is taken for division
8 × 9 = 72, 8 × 10 = 80
9H is quotient.
(ii) 76 - 72 = 4,
40 T is taken for division, 8 × 5 = 40
5T is quotient.
(iii) 08 is taken for division
8 × 1 = 8, 8 × 2 = 16,
1 is quotient.
Verification = 8 × 951 + 0 = 7608 + 0 = 7608.
Result is verified.
(v) 9575 ÷ 5
Check:
quotient × divisor = dividend
1915 × 5 = 9575
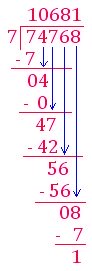
(vi) 74768 ÷ 7
Check:
quotient × divisor + remainder = dividend
1681 × 7 + 1 = 74768
4-Digit by 1-Digit Long Division Video
Subscribe to our YouTube channel for the latest videos, updates, and tips.
Worksheet on Division of 4-Digit by a 1-Digit Numbers:
1. Divide and find the quotient.
(i) 3,561 ÷ 2
(ii) 4,123 ÷ 3
(iii) 8,303 ÷ 5
(iv) 1,954 ÷ 7
(v) 7,050 ÷ 8
(vi) 8,754 ÷ 9
(vii) 4,327 ÷ 5
(viii) 3,510 ÷ 4
(ix) 4,160 ÷ 8
(x) 8,004 ÷ 6
(xi) 4,716 ÷ 9
(xii) 5,520 ÷ 4
Answer:
1. (i) Quotient: 1780 ; Remainder: 1
(ii) Quotient: 1374 ; Remainder: 1
(iii) Quotient: 1660 ; Remainder: 3
(iv) Quotient: 279 ; Remainder: 1
(v) Quotient: 881 ; Remainder: 2
(vi) Quotient: 972 ; Remainder: 6
(vii) Quotient: 865 ; Remainder: 2
(viii) Quotient: 877 ; Remainder: 2
(ix) Quotient: 520 ; Remainder: 0
(x) Quotient: 1334 ; Remainder: 0
(xi) Quotient: 520 ; Remainder: 0
(xii) Quotient: 1380 ; Remainder: 0
2. Find the quotient and the remainder. Also, check your answer.
(i) 3,504 ÷ 2
(ii) 1,352 ÷ 8
(iii) 2,316 ÷ 6
(iv) 7,626 ÷ 6
(v) 2,742 ÷ 6
(vi) 8,676 ÷ 4
(vii) 5,448 ÷ 8
(viii) 5,600 ÷ 7
Answer:
2. (i) Quotient: 1752 ; Remainder: 0
(ii) Quotient: 169 ; Remainder: 0
(iii) Quotient: 386 ; Remainder: 0
(iv) Quotient: 1271 ; Remainder: 0
(v) Quotient: 457 ; Remainder: 0
(vi) Quotient: 2169 ; Remainder: 0
(vii) Quotient: 681 ; Remainder: 0
(viii) Quotient: 800 ; Remainder: 0
You might like these
Terms Used in Division | Dividend | Divisor | Quotient | Remainder
The terms used in division are dividend, divisor, quotient and remainder. Division is repeated subtraction. For example: 24 ÷ 6 How many times would you subtract 6 from 24 to reach 0?
Successor and Predecessor | Successor of a Whole Number | Predecessor
The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number. For example, 9,99,99,999 is predecessor of 10,00,00,000 or we can also
Worksheets on Comparison of Numbers | Find the Greatest Number
In worksheets on comparison of numbers students can practice the questions for fourth grade to compare numbers. This worksheet contains questions on numbers like to find the greatest number, arranging the numbers etc…. Find the greatest number:
Number Worksheets | Practice Different Questions on Numbers | Answers
In number worksheets, students can practice different questions on numbers from printable free worksheets for grade 4 math on numbers. Write the number which is 1 more than 9? Write the number which
Comparison of Numbers | Compare Numbers Rules | Examples of Comparison
Rule I: We know that a number with more digits is always greater than the number with less number of digits. Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits. To learn
Formation of Numbers | Smallest and Greatest Number| Number Formation
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,
Formation of Numbers with the Given Digits |Making Numbers with Digits
In formation of numbers with the given digits we may say that a number is an arranged group of digits. Numbers may be formed with or without the repetition of digits.
Formation of Greatest and Smallest Numbers | Arranging the Numbers
the greatest number is formed by arranging the given digits in descending order and the smallest number by arranging them in ascending order. The position of the digit at the extreme left of a number increases its place value. So the greatest digit should be placed at the
Place Value and Face Value | Place and Face Value of Larger Number
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know that the position of a digit in a number determines its corresponding value
Expanded Form of a Number | Writing Numbers in Expanded Form | Values
We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its digits. This is shown here: In 2385, the place values of the digits are
Worksheet on Place Value | Place Value of a Digit in a Number | Math
Worksheet on place value for fourth grade math questions to practice the place value of a digit in a number. 1. Find the place value of 7 in the following numbers: (i) 7531 (ii) 5731 (iii) 5371
Worksheet on Expanded form of a Number | Expanded Form of a Number
Worksheet on expanded form of a number for fourth grade math questions to practice the expanded form according to the place values of its digit. 1. Write the expanded form of the following numbers
Examples on the Formation of Greatest and the Smallest Number |Example
In examples on the formation of greatest and the smallest number we know that the procedure of arranging the numbers in ascending and descending order.
Worksheet on Formation of Numbers | Questions on Formation of Numbers
In worksheet on formation of numbers, four grade students can practice the questions on formation of numbers without the repetition of the given digits. This sheet can be practiced by students
Rounding off Numbers | Nearest Multiple of 10 | Nearest Whole Number
Rounding off numbers are discussed here, where we need to round a number. (i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left. (ii) If we purchase another thing and its cost is $15.78. The cost is rounded up
Related Concept
● Addition
● Check for Subtraction and Addition
● Word Problems Involving Addition and Subtraction
● Estimating Sums and Differences
● Multiply a Number by a 2-Digit Number
● Multiplication of a Number by a 3-Digit Number
● Word Problems on Multiplication
● Division of Two-Digit by a One-Digit Numbers
● Division of Four-Digit by a One-Digit Numbers
● Division by 10 and 100 and 1000
● Division by Two-Digit Numbers
4th Grade Math Activities
From Division of Four-Digit by a One-Digit Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
5th Grade Temperature | Fahrenheit Scale | Celsius Scale | Thermometer
Jun 20, 25 12:58 PM
We will discuss here about the concept of temperature. We have already learned about various types of measurements like length, mass capacity and time. But if we have fever, non of these measurements -
Converting the Temperature from Fahrenheit to Celsius | Examples
Jun 20, 25 12:53 PM
In converting the temperature from Fahrenheit to Celsius the formula is, C = (5/9)(F - 32); The steps of converting from Fahrenheit to Celsius are reversed here. -
Converting the Temperature from Celsius to Fahrenheit | Examples
Jun 20, 25 12:01 PM
In converting the temperature from Celsius to Fahrenheit the formula is F = (9/5)C + 32. Steps of converting from Celsius (°C) to Fahrenheit (°F) -
Word Problems on Simple Interest | Simple Interest Formula | Worksheet
Jun 20, 25 01:12 AM
Word Problems on Simple Interest are solved here: 1. Robert deposits $ 3000 in State Bank of India for 3 year which earn him an interest of 8%.What is the amount -
Worksheet on Simple Interest | Word problem on Simple Interest | Free
Jun 19, 25 02:54 AM
In worksheet on simple interest we will get different types of question on calculating the simple interest, the principal amount, the rate of interest and the word problems on simple interest.
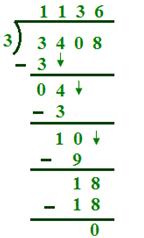
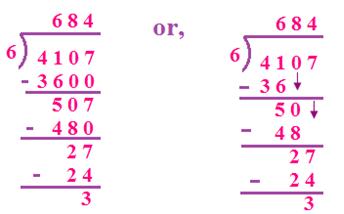
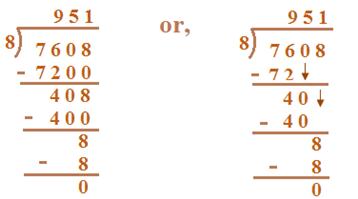
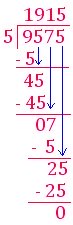
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.