Subscribe to our YouTube channel for the latest videos, updates, and tips.
Estimating the Quotient
We will learn estimating the quotient.
To estimate the quotient, we first round off the divisor and the dividend to the nearest tens, hundreds, or thousands and then divide the rounded numbers.
In a division sum, when the divisor is made up of 2 digits or more than 2 digits, it helps if we first estimate the quotient and then try to find the actual number.
(i) Divide 84 by 21
Round the number to the nearest ten
84 ÷ 21 → 80 ÷ 20
Calculate mentally.
8 ÷ 2 = 4
Estimated quotient = 4
(ii) 242 ÷ 22
Round to the nearest ten
240 ÷ 20
Calculate mentally
24 ÷ 2 = 12
Estimated quotient = 12
In
the process of division, the estimation of quotient plays a great role
in its solution. Let us see this in the following questions on division.
1. 74 ÷ 35
2. 627 ÷ 23
3. 694 ÷ 56
4. 975 ÷ 48
1. 74 ÷ 35 is approximately the same as 70 ÷ 40, i.e., 7 ÷ 4 (74 → 70 & 35 → 40)
7 ÷ 4 is approximately 2.
So, estimated quotient is 2.
2. 627 ÷ 23 is approximately the same as 600 ÷ 20 = 60 ÷ 2 = 30
(627 → 600 & 23 → 20)
So, the estimated quotient is 30.
3. 694 ÷ 56 is approximately the same as 700 ÷ 60 or 70 ÷ 6
70 ÷ 6 is approximately = 12.
So, the estimated quotient =12
4. 975 ÷ 48 is approximately 1000 ÷ 50 = 100 ÷ 5 = 20
So, estimated quotient = 20
Question and Answers on Estimation in Division:
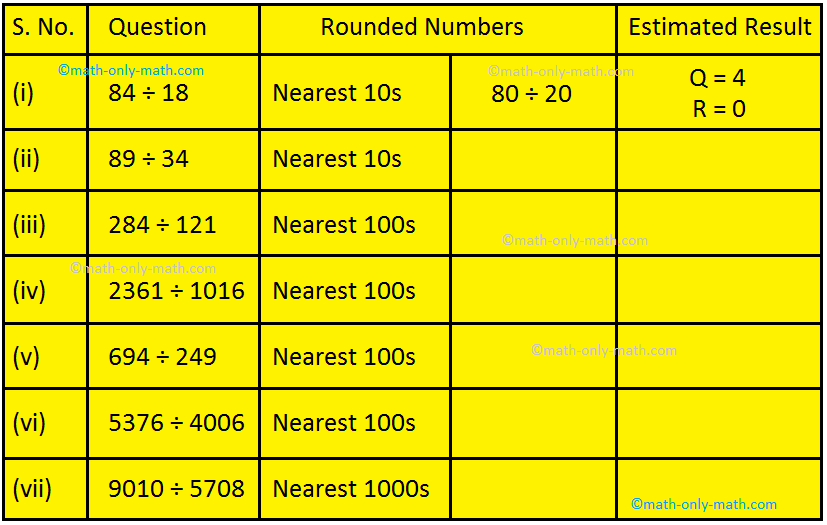
1. Estimate by rounding each number and then divide. One is done for you.
Answers:
(ii) 90 ÷ 30; Q = 3, R = 0
(iii) 300 ÷ 100; Q = 3, R = 0
(iv) 2400 ÷ 1000; Q = 2, R = 400
(v) 700 ÷ 200; Q = 3, R = 100
(vi) 5400 ÷ 4000; Q = 1, R = 1400
(vii) 9000 ÷ 6000; Q = 1, R = 3000
Related Concept
● Addition
● Check for Subtraction and Addition
● Word Problems Involving Addition and Subtraction
● Estimating Sums and Differences
● Multiply a Number by a 2-Digit Number
● Multiplication of a Number by a 3-Digit Number
● Word Problems on Multiplication
● Division of Two-Digit by a One-Digit Numbers
● Division of Four-Digit by a One-Digit Numbers
● Division by 10 and 100 and 1000
● Division by Two-Digit Numbers
4th Grade Math Activities
From Estimating the Quotient to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Expanded form of Decimal Fractions |How to Write a Decimal in Expanded
May 07, 25 01:48 AM
Decimal numbers can be expressed in expanded form using the place-value chart. In expanded form of decimal fractions we will learn how to read and write the decimal numbers. Note: When a decimal is mi… -
Dividing Decimals Word Problems Worksheet | Answers |Decimals Division
May 07, 25 01:33 AM
In dividing decimals word problems worksheet we will get different types of problems on decimals division word problems, dividing a decimal by a whole number, dividing a decimals and dividing a decima… -
How to Divide Decimals? | Dividing Decimals by Decimals | Examples
May 06, 25 01:23 AM
Dividing Decimals by Decimals I. Dividing a Decimal by a Whole Number: II. Dividing a Decimal by another Decimal: If the dividend and divisor are both decimal numbers, we multiply both the numbers by… -
Multiplying Decimal by a Whole Number | Step-by-step Explanation|Video
May 06, 25 12:01 AM
Multiplying decimal by a whole number is just same like multiply as usual. How to multiply a decimal by a whole number? To multiply a decimal by a whole number follow the below steps -
Word Problems on Decimals | Decimal Word Problems | Decimal Home Work
May 05, 25 01:27 AM
Word problems on decimals are solved here step by step. The product of two numbers is 42.63. If one number is 2.1, find the other. Solution: Product of two numbers = 42.63 One number = 2.1
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.