Terms Used in Division
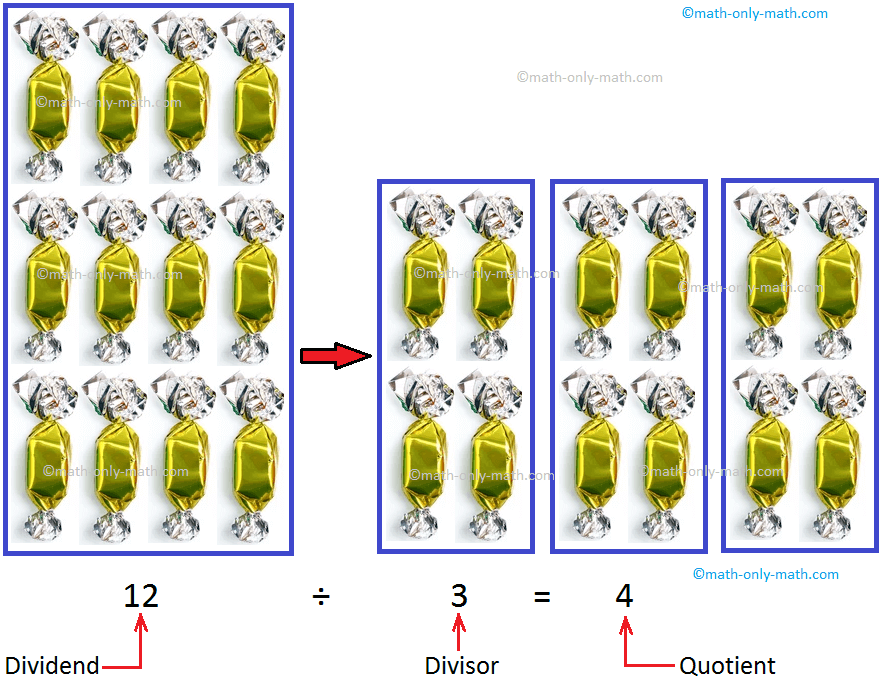
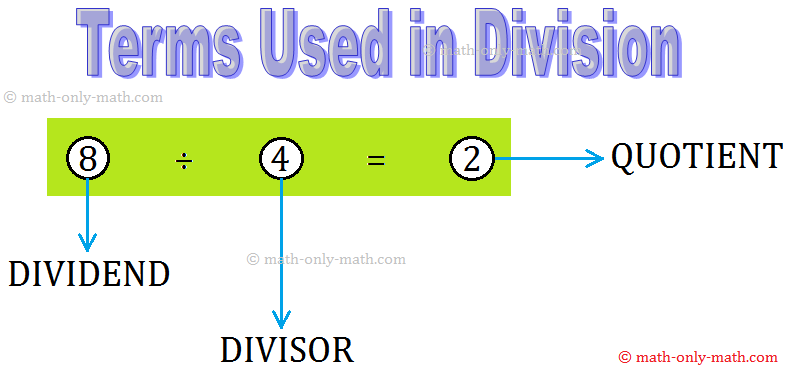
The terms used in division are dividend, divisor, quotient and remainder.
We know that divisor means to split a large group of objects into smaller equal groups. The larger group is called the dividend. The number of smaller equal groups is called the divisor and the number of objects in each smaller group is called the quotient.
Let us divide 12 candies among 3 children.
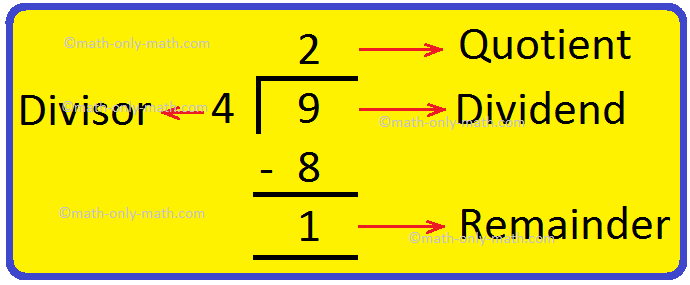
Now, let us divide 9 flowers into 2 equal groups.
When we cannot make equal groups or share equally all the objects, the number which is left undivided is called the remainder. Remainder is always less than the divisor.
Division is repeated subtraction.
For example:
24 ÷ 6
How many times would you subtract 6 from 24 to reach 0?
24 - 6 = 18 one time
18 - 6 = 12 two times
12 - 6 = 6 three times
6 - 6 = 0 four times
For every multiplication fact, there are two division facts.
For example:
(i) 5 × 7 = 35
35 ÷ 5 = 7; 35 ÷ 7 = 5
(ii) 8 × 6 = 48
48 ÷ 8 = 6; 48 ÷ 6 = 8
(iii) 9 × 5 = 45 is the same as 45 ÷ 9 = 5
7 × 9 = 63 is the same as 63 ÷ 7 = 9
Each of the terms used in division are explained below:
The number which is divided is called the dividend.
The number which divides is called the divisor.
The number which is the result of the division is called the quotient.
If there is any number left over, it is called the remainder.
The answer of a division operation can be verified in the following manner:
Quotient × Divisor + Remainder = Dividend
Consider the following examples to understand the terms showing in the division:
(i) 54 divided by 6
Dividend = Divisor × Quotient + Remainder
54 = 6 × 9 + 0
(ii) 81 divided by 9.
Dividend = Divisor × Quotient + Remainder
81 = 9 × 9 + 0
Properties of Division:
Let us recall the properties of division:
I: When the dividend is 0 and the divisor is a non-zero number, the quotient is 0.
(i) 0 ÷ 9 = 0
(ii) 0 ÷ 45 = 0
(iii) 0 ÷ 4524 = 0
II. When the divisor is 1, the quotient is the same number as the dividend.
(i) 8 ÷ 1 = 8
(ii) 77 ÷ 1 = 77
(iii) 4254 ÷ 1 = 4254
III. When the dividend and the divisor are the same non-zero number, the quotient is 1.
(i) 7 ÷ 7 = 1
(ii) 16 ÷ 16 = 1
(iii) 250 ÷ 250 = 1
SUMMERY
Terms Related to Division
In a division sum,
1. The number which is to be divided is called the dividend.
2. The number by which we divide is called the divisor.
3. The answer of division is called the quotient.
The above terms are interrelated as follows:
Dividend = Divisor × Quotient
The above relation is used to check the correctness of division problems.
The number being divided is called the dividend, the number dividing it is called the divisor and the result is called the quotient.
There is another way of showing this division.
This is called the long division method.
Worksheet on Terms Used in Division:
1. Now, complete the following table. One has been done for you:
|
Equation |
Dividend |
Divisor |
Quotient | |
|
(i) |
9 2)\(\overline{1 8}\) |
18 |
2 |
9 |
|
(ii) |
6 3)\(\overline{1 8}\) |
_____ |
_____ |
_____ |
|
(iii) |
3 5)\(\overline{1 5}\) |
_____ |
_____ |
_____ |
|
(iv) |
5 4)\(\overline{2 0}\) |
_____ |
_____ |
_____ |
|
(v) |
2 9)\(\overline{1 8}\) |
_____ |
_____ |
_____ |
Answer:
1. (ii) Dividend: 18; Divisor: 3; Quotient: 6
(iii) Dividend: 15; Divisor: 5; Quotient: 3
(iv) Dividend: 20; Divisor: 4; Quotient: 5
(v) Dividend: 18; Divisor: 9; Quotient: 2
2. Match the columns: Terms Used in Division
|
Quotient |
Question |
Remainder | |
|
(i) |
6 |
4|\(\overline{36}\) |
1 |
|
(ii) |
5 |
8|\(\overline{65}\) |
3 |
|
(iii) |
9 |
7|\(\overline{45}\) |
4 |
|
(iv) |
4 |
6|\(\overline{26}\) |
0 |
|
(v) |
8 |
9|\(\overline{49}\) |
2 |
Answer:
2. (i) 6 → 7|\(\overline{45}\) → 3
(ii) 5 → 9|\(\overline{49}\) → 4
(iii) 9 → 4|\(\overline{36}\) → 0
(iv) 4 → 6|\(\overline{26}\) → 2
(v) 8 → 8|\(\overline{65}\) → 1
3. Fill in the blanks:
(i) 15 ÷ 1 = _____
(ii) 21 ÷ _____ = 21
(iii) 12 ÷ _____ = 1
(iv) 0 ÷ 7 = _____
(v) 7 ÷ 1 = _____
(vi) 0 ÷ 20 = _____
(vii) 18 ÷ 18 = _____
(viii) 9 ÷ 0 = _____
(ix) 42 ÷ 42 = _____
Answer:
3. (i) 15
(ii) 1
(iii) 12
(iv) 0
(v) 7
(vi) 0
(vii) 1
(viii) undefined / meaningless
(ix) 1
1. What are the terms in division for class 4?
1. What are the terms in division for class 4?
Answer:
In the division sum,
• The number to be divided is called the dividend.
• The number with which we divide is called the divisor.
• The answer we get after division is called the quotient.
In a division sum, we write these term as:
Quotient
Divisor ) Dividend
You might like these
Successor and Predecessor | Successor of a Whole Number | Predecessor
The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number. For example, 9,99,99,999 is predecessor of 10,00,00,000 or we can also
Worksheets on Comparison of Numbers | Find the Greatest Number
In worksheets on comparison of numbers students can practice the questions for fourth grade to compare numbers. This worksheet contains questions on numbers like to find the greatest number, arranging the numbers etc…. Find the greatest number:
Number Worksheets | Practice Different Questions on Numbers | Answers
In number worksheets, students can practice different questions on numbers from printable free worksheets for grade 4 math on numbers. Write the number which is 1 more than 9? Write the number which
Comparison of Numbers | Compare Numbers Rules | Examples of Comparison
Rule I: We know that a number with more digits is always greater than the number with less number of digits. Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits. To learn
Formation of Numbers | Smallest and Greatest Number| Number Formation
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,
Formation of Numbers with the Given Digits |Making Numbers with Digits
In formation of numbers with the given digits we may say that a number is an arranged group of digits. Numbers may be formed with or without the repetition of digits.
Formation of Greatest and Smallest Numbers | Arranging the Numbers
the greatest number is formed by arranging the given digits in descending order and the smallest number by arranging them in ascending order. The position of the digit at the extreme left of a number increases its place value. So the greatest digit should be placed at the
Place Value and Face Value | Place and Face Value of Larger Number
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know that the position of a digit in a number determines its corresponding value
Expanded Form of a Number | Writing Numbers in Expanded Form | Values
We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its digits. This is shown here: In 2385, the place values of the digits are
Worksheet on Place Value | Place Value of a Digit in a Number | Math
Worksheet on place value for fourth grade math questions to practice the place value of a digit in a number. 1. Find the place value of 7 in the following numbers: (i) 7531 (ii) 5731 (iii) 5371
Worksheet on Expanded form of a Number | Expanded Form of a Number
Worksheet on expanded form of a number for fourth grade math questions to practice the expanded form according to the place values of its digit. 1. Write the expanded form of the following numbers
Examples on the Formation of Greatest and the Smallest Number |Example
In examples on the formation of greatest and the smallest number we know that the procedure of arranging the numbers in ascending and descending order.
Worksheet on Formation of Numbers | Questions on Formation of Numbers
In worksheet on formation of numbers, four grade students can practice the questions on formation of numbers without the repetition of the given digits. This sheet can be practiced by students
Rounding off Numbers | Nearest Multiple of 10 | Nearest Whole Number
Rounding off numbers are discussed here, where we need to round a number. (i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left. (ii) If we purchase another thing and its cost is $15.78. The cost is rounded up
Properties of Multiples | With Examples | Multiple of each Factor
The properties of multiples are discussed step by step according to its property. Every number is a multiple of 1. Every number is the multiple of itself. Zero (0) is a multiple of every number. Every multiple except zero is either equal to or greater than any of its factors
Related Concept
● Addition
● Check for Subtraction and Addition
● Word Problems Involving Addition and Subtraction
● Estimating Sums and Differences
● Multiply a Number by a 2-Digit Number
● Multiplication of a Number by a 3-Digit Number
● Word Problems on Multiplication
● Division of Two-Digit by a One-Digit Numbers
● Division of Four-Digit by a One-Digit Numbers
● Division by 10 and 100 and 1000
● Division by Two-Digit Numbers
From Terms Used in Division to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Fundamental Operations on Large Numbers Worksheet | 5th Grade Numbers
Mar 14, 25 05:31 PM
fundamental operations on large numbers worksheet -
Word Problems on Division | Examples on Word Problems on Division
Mar 13, 25 01:01 PM
Word problems on division for fourth grade students are solved here step by step. Consider the following examples on word problems involving division: 1. $5,876 are distributed equally among 26 men. H… -
Division of Whole Numbers |Relation between Dividend, Divisor Quotient
Mar 13, 25 12:41 PM
Relation between Dividend, Divisor, Quotient and Remainder is. Dividend = Divisor × Quotient + Remainder. To understand the relation between dividend, divisor, quotient and remainder let us follow the… -
Adding 1-Digit Number | Understand the Concept one Digit Number |Video
Mar 07, 25 03:55 PM
Understand the concept of adding 1-digit number with the help of objects as well as numbers. -
Vertical Addition | How to Add 1-Digit Number Vertically? | Problems
Mar 07, 25 02:35 PM
Now we will learn simple Vertical Addition of 1-digit number by arranging them one number under the other number. How to add 1-digit number vertically?
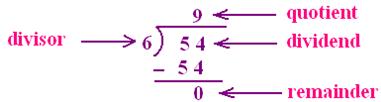
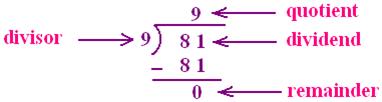
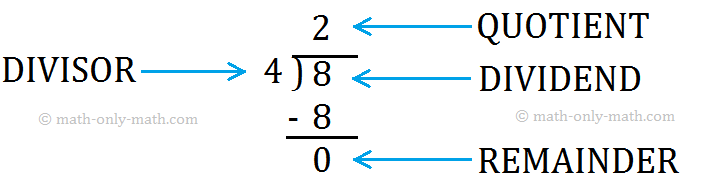
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.