Long Division
As we know that the division is to distribute a given value or quantity into groups having equal values. In long division, values at the individual place (Thousands, Hundreds, Tens, Ones) are dividend one at a time starting with the highest place.
We know, to divide 24 by 4, we write 24 ÷ 4.
We can also arrange these numbers as shown
Divisor (4) \(\overline{) Dividend (24)}\)
Then we use the multiplication table of 4 to find the quotient.
4 × 6 = 24
The above form of finding quotient is called long division method.
Remember:
Long division method helps to divide bigger numbers easily.
Long Division of 2 Digit Number by 1 Digit Number:
Division can be shown in two ways. e.g. Short form and Long form.
LONG DIVISION METHOD
|
Division fact 24 ÷ 8 = 3 can also be written as |
 |
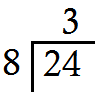This is called long form of division.
Some more examples of writing division facts in long form are given below:
Terms Related to Division:
There are mainly three terms related to long division method.These are divisor, dividend and quotient.
For example, 32 ÷ 4 = 8 is written in long form as:
Dividend = Divisor x Quotient
This equation can be used to check whether we have carried out division correctly or not.
For example, in the above example:
Dividend = 4 × 8 = 32.
Hence, the division is correct.
A. Division by One-Digit Divisor
1. Divide 27 by 9
Solution:
Let us divide.
|
Step I: Write 27 inside the bracket and 9 on the left side of the bracket. Step II: Start division from left to right, that is, divide 2 by 9. Since, we cannot divide 2 by 9 so, we will divide 27 by 9. Step III: Recall the table of 9. 9 × 3 = 27 Now, write 3 in the quotient and subtract 27 from 27. The result is 0. Thus, 27 ÷ 9 = 3 |
2. Divide 92 by 4
Solution:
Let us divide.
|
Step I: Write 92 inside the bracket and 4 on the left side of the bracket. Step II: Start division from left to right, that is, divide 9 tens by 4. 4 × 2 = 8 4 × 3 = 12 12 tens is bigger than 9 tens, so we take 4 × 2 = 8 tens. Step III: Write 2 in the quotient. Step IV: Subtract 8 from 9 and get 1 as remainder. Step V: Bring down 2 from ones place and write it to the right of 1. 12 is the new dividend. Step VI: Write 3 in the quotient and subtract 12 from 12. The result is 0. Thus, 92÷4 = 23 |
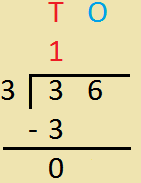
3. Divide 36 by 3.
|
3 × 1 = 3 Write 1 as a quotient write 3 under 3 and subtract | |
|
Bring down 6 ones. Now divide 6 by 3 3 × 2 = 6 Write 2 as a quotient and write 6 under the new dividend and subtract Now, 36 divided by 3 is 12. |
4. Divide 30 by 5.
Notes:
I. Divide the Tens.
II. Then, divide the Ones.
B. Division of 3-Digit Number by One-Digit Number:
1. Divide 324 by 2.
First Divide the Hundreds
|
Dividing Hundreds Divide 6 H by 2 = 3H write 3 in place of quotient and 6 under 6 and subtract 6 - 6=0 |
Then, Divide the Tens.
|
Dividing Tens Now, bring down 4 T. Divide 4 T by 2 = 2T write 2 in tens place of the quotient and 4 under 4 then subtract 4 - 4 = 0 |
Finally, Divide the Ones.
|
Dividing Ones Bring down 8 Ones. Divide 8 ones by 2 = 4 ones write 4 in the ones place of the quotient. write 8 under 8 and subtract 8 - 8 = 0 |
D. Division of 4-Digits Number by 1-Digit Number:
To divide 4-Digit numbers follow these steps -
(i) Divide the Thousands.
(ii) Divide the Hundreds.
(iii) Divide the Tens.
(iv) Divide the Ones.
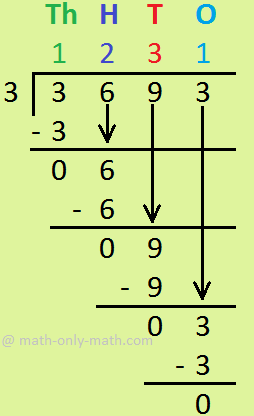
1. Divide 3693 by 3.
|
Step I: Dividing Thousands Divide 3 Th by 3 = 1Th write 1 in place of quotient and 3 under 3 and subtract 3 - 3 =0 Step II: Dividing Hundreds Bring down 6 H. Divide 6 H by 3 = 2H write 2 in place of quotient and 6 under 6 and subtract 6 - 6=0 Step III: Dividing Tens Now, bring down 9 T. Divide 9 T by 3 = 3T write 3 in tens place of the quotient and 9 under 9 then subtract 9 - 9 = 0 Step IV: Dividing Ones Bring down 3 Ones. Divide 3 ones by 3 = 1 ones write 1 in the ones place of the quotient. write 3 under 3 and subtract 3 - 3 = 0 |
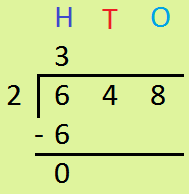
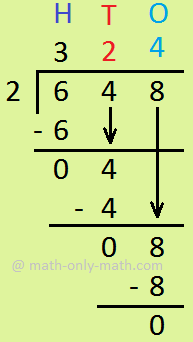
2. Divide 6428 by 2.
|
Step I: Dividing Thousands Divide 6 Th by 2 = 3Th write 3 in place of quotient and 6 under 6 and subtract 6 - 6 =0 Step II: Dividing Hundreds Bring down 4 H. Divide 4 H by 2 = 2H write 2 in place of quotient and 4 under 4 and subtract 4 - 4=0 Step III: Dividing Tens Now, bring down 2 T. Divide 2 T by 2 = 1T write 1 in tens place of the quotient and 2 under 2 then subtract 2 - 2 = 0 Step IV: Dividing Ones Bring down 8 Ones. Divide 8 ones by 2 = 4 ones write 4 in the ones place of the quotient. write 8 under 8 and subtract 8 - 8 = 0 |
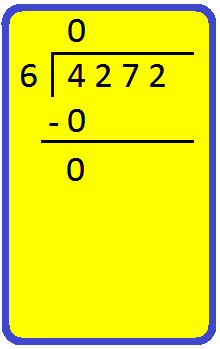
2. Divide 4,272 by 6.
Step I: Arrange the numbers as shown.
|
Step II: We begin from left. i.e., with thousands. Divide 4 thousands by 6. Also, 6 × 1 = 6. But, 6 > 4. So, we take 6 × 0 = 0. Write 0 in the thousands place of the quotient and 0 below 4. Subtract 0 from 4. |
|
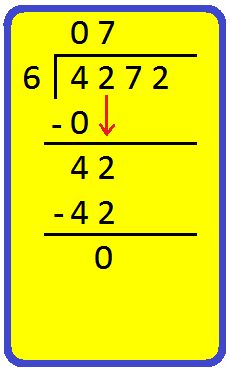
Step III: Bring down 2 and divide 42 by 6. Also, 6 × 7 = 42. So, wine 7 in the hundreds place of the quotient and 42 below 42. Subtract 42 from 42. |
|
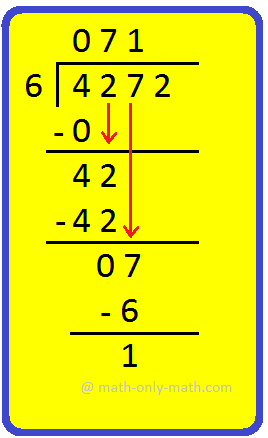
Step IV: Bring down 7 and divide it by 6. Also 6 × 1 = 6. So, write 1 in the tens place of the quotient and 6 below 7. Subtract 6 from 7. |
Step V: Bring down 2 and divide 12 by 6.
Also 6 × 2 = 12.
So, write 2 in the ones place of the quotient and 12 below 12.
Subtract 12 from 12
Thus 4,272 ÷ 6 = 712 and remainder = 0
Division with Remainder:
1. Divide 49 by 4.
|
T: 4 ÷ 4 = 1. Quotient = 1 O: 9 ÷ 4= ? 4 × 2 = 8 (nearest number) 9 - 8 = 1 So, Quotient = 2 Remainder = 1 |
Divisor - 4, Quotient - 12, Remainder - 1.
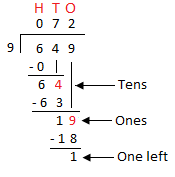
2. Find the quotient and remainder of 649 ÷ 9.
Solution:
|
Step I: We start dividing the hundreds first. Since 6 hundreds cannot be divided into 9 groups of hundreds, the quotient at hundreds column is zero. Step II: 6 Hundreds are now changed into 60 tens and added to 4 tens, making 64 tens. Step III: 64 tens give 9 groups of 7 tens each and 1 ten is left over. Step IV: 1 ten give 10 ones, 10 ones + 9 ones = 19 ones Step V: 19 ones can be put into 2 groups of 9 and 1 one is left over. |
 q = 72; r = 1 |
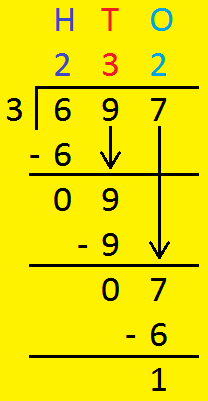
3. Divide 697 by 3.
|
H: 6 ÷ 3 = 2. T: 9 ÷ 3 = 3. O: 7 ÷ 3 = ? 3 × 2 = 6 (nearest number) 7 - 6 = 1 So, in O Quotient = 2 Remainder = 1 |
Divisor - 3, Quotient - 232, Remainder 1.
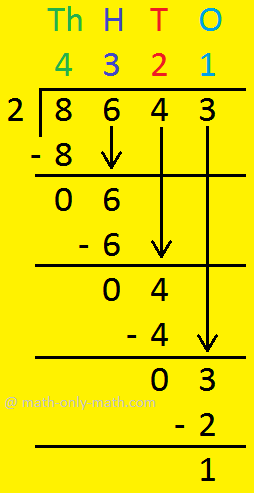
4. Divide 8643 by 2.
|
Th: 8 ÷ 2 = 4 H: 6 ÷ 2 = 3 T: 4 ÷ 2 = 2 O: 3 ÷ 2 = ? 2 × 1 = 2 3 - 2 = 1 So. in O Quotient = 2 Remainder = 1 |
Divisor - 2, Quotient - 4321, Remainder 1.
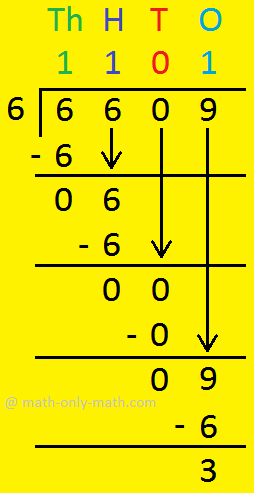
5. Divide 6609 by 6.
|
Th: 6 ÷ 6 = 1 H: 6 ÷ 6 = 1 T: 0 ÷ 6 = 0 O: 9 ÷ 6 = ? 6 × 1 = 6 9 - 6 = 3 So, in Quotient = 1 Remainder = 3 |
Divisor - 6, Quotient - 1101, Remainder 3.
E. Division with Regrouping:
1. Divide 96 by 4.
|
Step I: Dividing Tens Divide 9 ÷ 4 = ? 4 × 2 = 8 8 < 9 4 × 3 = 12 12 > 9 we use 4 × 2 = 8. write 2 in tens place of the quotient and 8 below 9 then subtract 9 - 8 = 1 |
|
Step II: Dividing Ones Bring down 6 Ones, we have 16 ones 1 ten+ 6 ones. Divide 16 ones ÷ 4 4 × 4 = 16 write 4 in ones place of the quotient and 16 below 16 Now, 16 - 16 = 0 |
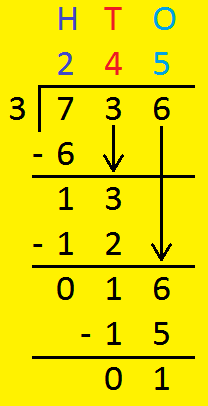
2. Divide 736 by 3.
|
H: 7 ÷ 3 = ?. So, 3 × 2 =6 Q: 2; R: 7 - 6 = 1 or 1 hundreds Regroup - 1 hundreds and 3 tens = 13 tens T: 13 + 3 = ?. So, 3 × 4 = 12 Q: 4; R: 13 - 12 = 1 or 1 tens Regroup - 1 tens and 5 ones = 15 ones O: 16 ÷ 3 = ?. So, 3 × 5 = 15 Q: 5; R: 16 - 15 = 1 Remainder - 1 |
Here 3 is divisor, 736 is dividend, 245 is quotient and 1 is remainder.
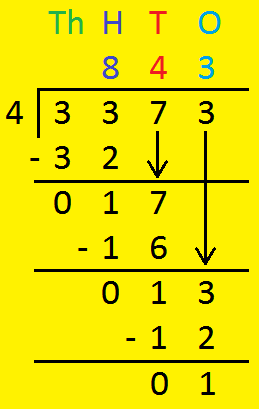
3. Divide 3373 by 4.
|
Th: 3 < 4 so 3 + 4 is not possible. Regroup - 3 thousands and 3 hundreds = 33 hundreds H:33 ÷ 4 = ? Q: 8; R: 33 - 32 = 1 Remainder - 1 hundreds Regroup - 1 hundreds and 7 tens = 17 tens T: 17 ÷ 4 = 4 Q: 4 R: 17 - 16 = 1 Remainder - 1 tens Regroup - 1 tens and 3 ones = 13 ones O:13 ÷ 4 = 3 Q: 3 R: 13 - 12 = 1 Remainder - 1 |
Here 4 is divisor, 3373 is dividend, 845 is quotient and 1 is remainder.
Keep in Mind
- First, divide the Thousands.
- Then, divide the Hundreds. Then, divide the Tens.
- Finally, divide the Ones.
Division by Two-Digit Divisors
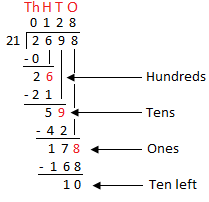
1. Divide 2698 by 21.
Solution:
Recall the process of long division.
|
Step I: 2 thousands cannot be divided into 21 groups of thousand. So, 0 is placed as quotient in the thousands column. Step II: 2 thousands give 20 hundreds. 20 hundreds + 6 hundreds give 26 hundreds. 26 hundreds make 1 group of 21 hundreds. 5 hundreds are left. Step III: 5 hundreds give 50 tens. |
 q = 128; r = 10 |
So, 50 tens + 9 tens = 59 tens
59 tens are to be divided into 21 groups of tens
59 tens ÷ 21 makes 2 groups with 17 tens left.
2 is placed in the quotient in the tens column.
Step IV: 17 tens = 170 ones
170 ones + 8 ones = 178 ones
178 ones ÷ 21 makes 8 groups with 10 ones left.
Thus, in division of 2,698 by 21, we get 128 as quotient and 10 as remainder.
Word Problems on Long Division:
To solve any word problem, we need to read each word carefully and select numbers carefully from the question to solve it.
1. If 60 cookies to be put in 5 packets, how many cookies will be packed in one packet?
|
Solution: Number of cookies = 60 cookies Equally distributed in 5 packets Number of cookies in one packet = 60 ÷ 5 |
Thus, 12 cookies will be packed in one packet.
2. A bottle of coke costs $ 8. How many bottles of coke can be bought for $ 96?
|
Solution: Total cost of bottles purchased = $ 96 Cost of one bottle = $ 8 Number of bottles purchased = 96 ÷ 8 = 12 Hence, 12 bottles can be bought for $ 96. |
Questions and Answers on Long Division:
A. Division of 2 Digit Number by 1 Digit Number:
I. Divide and find the quotient:
(i) 85 ÷ 5 = _____
(ii) 54 ÷ 3 = _____
(iii) 63 ÷ 7 = _____
(iv) 60 ÷ 3 = _____
(v) 42 ÷6 = _____
(vi) 32 ÷ 8 = _____
(vii) 88 ÷ 8 = _____
(viii) 69 ÷ 3 = _____
(ix) 48 ÷ 3 = _____
(x) 42 ÷ 6 = _____
(xi) 68 ÷ 4 = _____
(xii) 96 ÷ 6 = _____
(xiii) 86 ÷ 2 = _____
(xiv) 36 ÷ 9 = _____
(xv) 77 ÷ 7 = _____
(xvi) 63 ÷ 3 = _____
(xvii) 22 ÷ 2 = _____
(xviii) 72 ÷ 9 = _____
(xix) 33 ÷ 3 = _____
(xx) 68 ÷ 2 = _____
Answer:
I. (i) 17
(ii) 18
(iii) 9
(iv) 20
(v) 7
(vi) 4
(vii) 11
(viii) 23
(ix) 16
(x) 7
(xi) 17
(xii) 16
(xiii) 43
(xiv) 4
(xv) 11
(xvi) 21
(xvii) 11
(xviii) 8
(xix) 11
(xx) 34
II. Find the quotient:
|
(i) |
3 |\(\overline{2 7}\) |
(ii) |
7 |\(\overline{4 2}\) |
|
(iii) |
8 |\(\overline{6 4}\) |
(iv) |
2 |\(\overline{1 8}\) |
|
(v) |
3 |\(\overline{2 1}\) |
(vi) |
9 |\(\overline{8 1}\) |
|
(vii) |
5 |\(\overline{3 5}\) |
(viii) |
6 |\(\overline{4 8}\) |
|
(ix) |
4 |\(\overline{3 6}\) |
(x) |
7 |\(\overline{6 3}\) |
|
(xi) |
3 |\(\overline{9 3}\) |
(xii) |
2 |\(\overline{8 2}\) |
|
(xiii) |
2 |\(\overline{2 6}\) |
(xiv) |
2 |\(\overline{1 0}\) |
|
(xv) |
3 |\(\overline{3 0}\) |
(xvi) |
7 |\(\overline{4 9}\) |
|
(xvii) |
2 |\(\overline{6 4}\) |
(xviii) |
8 |\(\overline{7 2}\) |
|
(xix) |
7 |\(\overline{7 7}\) |
(xx) |
8 |\(\overline{4 8}\) |
Answer:
II. (i) 9
(ii) 6
(iii) 8
(iv) 9
(v) 7
(vi) 9
(vii) 7
(viii) 8
(ix) 9
(x) 9
(xi) 31
(xii) 41
(xiii) 13
(xiv) 5
(xv) 10
(xvi) 7
(xvii) 32
(xviii) 9
(xix) 11
(xx) 6
B. Long Division of 3-Digit Number by 1-Digit Number:
III. Divide and find the quotients -
(i) 246 ÷ 2 = _____
(ii) 666 ÷ 6 = _____
(iii) 339 ÷ 3 = _____
(iv) 936 ÷ 3 = _____
(v) 648 ÷ 2 = _____
(vi) 222 ÷ 2 = _____
(vii) 242 ÷ 2 = _____
(viii) 777 ÷ 7 = _____
(ix) 480 ÷ 2 = _____
(x) 420 ÷ 2 = _____
(xi) 848 ÷ 2 = _____
(xii) 399 ÷ 3 = _____
(xiii) 448 ÷ 4 = _____
(xiv) 224 ÷ 2 = _____
(xv) 960 ÷ 3 = _____
(xvi) 848 ÷ 4 = _____
(xvii) 402 ÷ 2 = _____
(xviii) 636 ÷ 3 = _____
(xix) 939 ÷ 3 = _____
(xx) 444 ÷ 4 = _____
Answer:
III. (i) 123
(ii) 111
(iii) 113
(iv) 312
(v) 324
(vi) 111
(vii) 121
(viii) 111
(ix) 240
(x) 210
(xi) 424
(xii) 133
(xiii) 112
(xiv) 112
(xv) 320
(xvi) 212
(xvii) 201
(xviii) 212
(xix) 313
(xx) 111
IV. Find the quotient:
|
(i) |
4 |\(\overline{804}\) |
(ii) |
3 |\(\overline{363}\) |
|
(iii) |
4 |\(\overline{408}\) |
(iv) |
2 |\(\overline{826}\) |
|
(v) |
2 |\(\overline{604}\) |
(vi) |
3 |\(\overline{336}\) |
|
(vii) |
8 |\(\overline{888}\) |
(viii) |
4 |\(\overline{484}\) |
|
(ix) |
3 |\(\overline{993}\) |
(x) |
4 |\(\overline{884}\) |
|
(xi) |
5 |\(\overline{555}\) |
(xii) |
2 |\(\overline{484}\) |
|
(xiii) |
3 |\(\overline{366}\) |
(xiv) |
2 |\(\overline{442}\) |
|
(xv) |
2 |\(\overline{882}\) |
(xvi) |
3 |\(\overline{663}\) |
|
(xvii) |
2 |\(\overline{866}\) |
(xviii) |
9 |\(\overline{999}\) |
|
(xix) |
2 |\(\overline{224}\) |
(xx) |
3 |\(\overline{333}\) |
Answer:
IV. (i) 201
(ii) 121
(iii) 102
(iv) 413
(v) 302
(vi) 112
(vii) 111
(viii) 121
(ix) 331
(x) 221
(xi) 111
(xii) 242
(xiii) 122
(xiv) 221
(xv) 441
(xvi) 221
(xvii) 433
(xviii) 111
(xix) 112
(xx) 111
C. Long Division of 4-Digit Number by 1-Digit Number:
V. Divide and find the quotients -
(i) 7777 ÷ 7 = _____
(ii) 4884 ÷ 2 = _____
(iii) 6699 ÷ 3 = _____
(iv) 9999 ÷ 3 = _____
(v) 6666 ÷ 2 = _____
(vi) 9969 ÷ 3 = _____
(vii) 4002 ÷ 2 = _____
(viii) 2468 ÷ 2 = _____
(ix) 4884 ÷ 4 = _____
(x) 6844 ÷ 2 = _____
(xi) 2244 ÷ 2 = _____
(xii) 6969 ÷ 3 = _____
(xiii) 8844 ÷ 2 = _____
(xiv) 8084 ÷ 4 = _____
(xv) 6060 ÷ 3 = _____
(xvi) 4444 ÷ 2 = _____
(xvii) 6448 ÷ 2 = _____
(xviii) 9060 ÷ 3 = _____
(xix) 4488 ÷ 2 = _____
(xx) 6666 ÷ 3 = _____
(xxi) 8888 ÷ 4 = _____
(xxii) 8888 ÷ 2 = _____
(xxiii) 9966 ÷ 3 = _____
(xxiv) 4488 ÷ 4 = _____
Answer:
V. (i) 1111
(ii) 2442
(iii) 2233
(iv) 3333
(v) 3333
(vi) 3323
(vii) 2001
(viii) 1234
(ix) 1221
(x) 3422
(xi) 1122
(xii) 2323
(xiii) 4422
(xiv) 2021
(xv) 2020
(xvi) 2222
(xvii) 3224
(xviii) 3020
(xix) 2244
(xx) 2222
(xxi) 2222
(xxii) 4444
(xxiii) 3322
(xxiv) 1122
VI. Find the Quotient:
|
(i) |
2 |\(\overline{2424}\) |
(ii) |
3 |\(\overline{3939}\) |
|
(iii) |
4 |\(\overline{8484}\) |
(iv) |
2 |\(\overline{4242}\) |
|
(v) |
5 |\(\overline{5505}\) |
(vi) |
8 |\(\overline{4848}\) |
|
(vii) |
7 |\(\overline{4956}\) |
(viii) |
9 |\(\overline{8136}\) |
|
(ix) |
2 |\(\overline{2826}\) |
(x) |
3 |\(\overline{3639}\) |
|
(xi) |
2 |\(\overline{8448}\) |
(xii) |
3 |\(\overline{3036}\) |
|
(xiii) |
2 |\(\overline{8468}\) |
(xiv) |
4 |\(\overline{8448}\) |
|
(xv) |
3 |\(\overline{3363}\) |
(xvi) |
6 |\(\overline{6636}\) |
Answer:
VI. (i) 1212
(ii) 1313
(iii) 2121
(iv) 2121
(v) 1101
(vi) 606
(vii) 708
(viii) 904
(ix) 1413
(x) 1213
(xi) 4224
(xii) 1012
(xiii) 4234
(xiv) 2112
(xv) 1121
(xvi) 1106
D. Long Division with Remainder:
VII. Divide and find the quotients and remainders -
(i) 96 ÷ 3 = _____
(ii) 89 ÷ 4 = _____
(iii) 45 ÷ 4 = _____
(iv) 65 ÷ 2 = _____
(v) 37 ÷ 3 = _____
(vi) 63 ÷ 2 = _____
(vii) 27 ÷ 4 = _____
(viii) 95 ÷ 3 = _____
(ix) 849 ÷ 4 = _____
(x) 807 ÷ 4 = _____
(xi) 847 ÷ 4 = _____
(xii) 638 ÷ 3 = _____
(xiii) 4849 ÷ 2 = _____
(xiv) 2427 ÷ 2 = _____
(xv) 9634 ÷ 3 = _____
(xvi) 4846 ÷ 4 = _____
(xvii) 8485 ÷ 4 = _____
(xviii) 6937 ÷ 3 = _____
(xix) 5556 ÷ 5 = _____
(xx) 9695 ÷ 3 = _____
Answer:
VII. (i) Quotient: 32; Remainder: 0
(ii) Quotient: 22; Remainder: 1
(iii) Quotient: 11; Remainder: 1
(iv) Quotient: 32; Remainder: 1
(v) Quotient: 12; Remainder: 1
(vi) Quotient: 31; Remainder: 1
(vii) Quotient: 6; Remainder: 3
(viii) Quotient: 31; Remainder: 2
(ix) Quotient: 212; Remainder: 1
(x) Quotient: 201; Remainder: 3
(xi) Quotient: 211; Remainder: 3
(xii) Quotient: 212; Remainder: 2
(xiii) Quotient: 2424; Remainder: 1
(xiv) Quotient: 1213; Remainder: 1
(xv) Quotient: 3211; Remainder: 1
(xvi) Quotient: 1211; Remainder: 2
(xvii) Quotient: 2121; Remainder: 1
(xviii) Quotient: 2312; Remainder: 1
(xix) Quotient: 1111; Remainder: 1
(xx) Quotient: 3231; Remainder: 2
VIII. Find the Quotients and remainders:
|
(i) |
2 |\(\overline{25}\) |
(ii) |
4 |\(\overline{87}\) |
|
(iii) |
6 |\(\overline{669}\) |
(iv) |
2 |\(\overline{889}\) |
|
(v) |
3 |\(\overline{965}\) |
(vi) |
3 |\(\overline{397}\) |
|
(vii) |
4 |\(\overline{849}\) |
(viii) |
5 |\(\overline{556}\) |
|
(ix) |
2 |\(\overline{245}\) |
(x) |
3 |\(\overline{668}\) |
|
(xi) |
2 |\(\overline{667}\) |
(xii) |
2 |\(\overline{887}\) |
|
(xiii) |
3 |\(\overline{6968}\) |
(xiv) |
2 |\(\overline{4829}\) |
|
(xv) |
4 |\(\overline{4889}\) |
(xvi) |
2 |\(\overline{8267}\) |
Answer:
VIII. (i) Quotient: 12; Remainder: 1
(ii) Quotient: 21; Remainder: 3
(iii) Quotient: 111; Remainder: 3
(iv) Quotient: 444; Remainder: 1
(v) Quotient: 321; Remainder: 2
(vi) Quotient: 132; Remainder: 1
(vii) Quotient: 212; Remainder: 1
(viii) Quotient: 111; Remainder: 1
(ix) Quotient: 122; Remainder: 1
(x) Quotient: 222; Remainder: 2
(xi) Quotient: 333; Remainder: 1
(xii) Quotient: 443; Remainder: 1
(xiii) Quotient: 2322; Remainder: 2
(xiv) Quotient: 4214; Remainder: 1
(xv) Quotient: 1222; Remainder: 1
(xvi) Quotient: 4133; Remainder: 1
D. Long Division with Regrouping:
IX. Find the quotients and remainders of these sums -
(i) 84 ÷ 7 = _____
(ii) 96 ÷ 5 = _____
(iii) 99 ÷ 8 = _____
(iv) 81 ÷ 3 = _____
(v) 76 ÷ 4 = _____
(vi) 53 ÷ 2 = _____
(vii) 95 ÷ 4 = _____
(viii) 67 ÷ 5 = _____
(ix) 711 ÷ 9 = _____
(x) 207 ÷ 3 = _____
(xi) 776 ÷ 8 = _____
(xii) 441 ÷ 7 = _____
(xiii) 920 ÷ 8 = _____
(xiv) 607 ÷ 5 = _____
(xv) 534 ÷ 5 = _____
(xvi) 7284 ÷ 3 = _____
(xvii) 2389 ÷ 4 = _____
(xviii) 6700 ÷ 9 = _____
(xix) 8489 ÷ 7 = _____
(xx) 9900 ÷ 8 = _____
Answer:
IX. (i) Quotient: 12; Remainder: 0
(ii) Quotient: 19; Remainder: 1
(iii) Quotient: 12; Remainder: 3
(iv) Quotient: 27; Remainder: 0
(v) Quotient: 19; Remainder: 0
(vi) Quotient: 26; Remainder: 1
(vii) Quotient: 23; Remainder: 3
(viii) Quotient: 13; Remainder: 2
(ix) Quotient: 79; Remainder: 0
(x) Quotient: 69; Remainder: 0
(xi) Quotient: 97; Remainder: 0
(xii) Quotient: 63; Remainder: 0
(xiii) Quotient: 115; Remainder: 0
(xiv) Quotient: 121; Remainder: 2
(xv) Quotient: 106; Remainder: 4
(xvi) Quotient: 2428; Remainder: 0
(xvii) Quotient: 597; Remainder: 1
(xviii) Quotient: 744; Remainder: 4
(xix) Quotient: 1212; Remainder: 5
(xx) Quotient: 1237; Remainder: 4
X. Find the Quotients and remainders:
|
(i) |
3 |\(\overline{57}\) |
(ii) |
4 |\(\overline{62}\) |
|
(iii) |
5 |\(\overline{77}\) |
(iv) |
4 |\(\overline{68}\) |
|
(v) |
7 |\(\overline{85}\) |
(vi) |
2 |\(\overline{314}\) |
|
(vii) |
4 |\(\overline{973}\) |
(viii) |
5 |\(\overline{630}\) |
|
(ix) |
6 |\(\overline{746}\) |
(x) |
5 |\(\overline{6795}\) |
|
(xi) |
7 |\(\overline{9395}\) |
(xii) |
8 |\(\overline{9985}\) |
Answer:
X. (i) Quotient: 19; Remainder: 0
(ii) Quotient: 15; Remainder: 2
(iii) Quotient: 15; Remainder: 2
(iv) Quotient: 17; Remainder: 0
(v) Quotient: 12; Remainder: 1
(vi) Quotient: 157; Remainder: 0
(vii) Quotient: 243; Remainder: 1
(viii) Quotient: 126; Remainder: 0
(ix) Quotient: 124; Remainder: 2
(x) Quotient: 1359; Remainder: 0
(xi) Quotient: 1342; Remainder: 1
(xii) Quotient: 1248; Remainder: 1
XI. Solve the given word problems on long division.
1. Shelly has 75 pencils. She shares them between her 5 friends. How many pencils will each of her friend get?
2. In class III, there are total 70 children. If there are 5 sections in class III, how many children are there in each section?
3. There are 68 birds in a zoo in 4 cages. How many birds are there in each cage?
4. Jack, the clown has 99 balloons which he needs to share between 9 children at the fair. How many balloons does each child get?
5. Nancy has 96 pieces of candy. She has 8 bags. She wants to put the same amount of candies in each bag. How many will she put in each bag?
6. Mike organised 24 chairs in 4 rows for a party. How many chairs are there in each row?
7. You have 60 gum balls that you need to share equally in five containers. How many gum balls will be in each container?
8. There are 96 books on the shelf. If the books are to be shared equally amongst 4 table groups in the class, how many books will be there on each table?
9. Amit walks 4 km. in one hour. How long will he take to cover 48 kilometers?
10. 3 toy-guns cost $ 369. What is the cost of one toy-gun?
11. The rent of a house for 6 months is $ 6666. What is the rent for one month?
12. 68 players were divided equally into 6 teams. How many players were there in each team and how many were left without any team?
13. 609 flowers were divided to make 6 garlands. How many flowers were used in each garland and how many flowers are left now?
14. 441 sheets were divided equally to make 2 books. How many sheets were used for each book and how many sheets were left?
15. 4 pens cost $ 56. What is the cost of one pen?
16. 750 students were divided into 5 equal houses. How many students are there in each house?
17. A housing society, consisting of 4 towers, has 1016 sparking lights for decoration in Diwali. How many lights will be used in each tower?
18. Rohit has 79 marbles with him. He groups them into sets of 5 each. How many sets of marbles did he make and how many marbles are left?
19. A fruit-seller has 364 oranges. He puts them equally into 5 boxes. How many oranges does he put into each box and how many are left?
20. 9 cans of milk can be carried in one van. If there are 1360 cans, how many vans are required and how many cans will be left behind?
21. Ten trucks carry 9000 crates of coke. How many crates does each truck carry?
Answer:
XI. 1. 15
2. 14
3. 17
4. 11
5. 12
6. 6
7. 12
8. 24
9. 12
10. $123
11. $ 1111
12. 11; 2
13. 101; 3
14. 220; 1
15. $ 14
16. 150
17. 254
18. 15; 4
19. 72; 4
20. 151; 1
21. 900
You might like these
Facts about Division | Basic Division Facts | Learn Long Division
We have already learned division by repeated subtraction, equal sharing/distribution and by short division method. Now, we will read some facts about division to learn long division. 1. If the dividend is ‘zero’ then any number as a divisor will give the quotient as ‘zero’.
Multiplying 3-Digit Number by 1-Digit Number | Three-Digit Multiplicat
Here we will learn multiplying 3-digit number by 1-digit number. In two different ways we will learn to multiply a two-digit number by a one-digit number. 1. Multiply 201 by 3 Step I: Arrange the numbers vertically. Step II: Multiply the digit at the ones place by 3.
Worksheet on Subtraction Word Problems | Subtraction Word Problems
The activity provided in the third grade math worksheet on subtraction word problems is very important for the kids. Students need to read the questions carefully and then translate the information
Subtraction of 3-Digit Numbers with Regrouping | Step-by-Step Explanat
Subtraction of 3-digit numbers with regrouping are explained here with examples. As you borrow from the tens column, you can borrow from the hundreds column also. 1 ten = 10 ones 1 hundred = 10 tens
Addition of Three 3-Digit Numbers | With and With out Regrouping |Math
Without regrouping: Adding three 3-digit numbers is same as adding two 3-digit numbers.
From Long Division to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
Dec 13, 24 08:43 AM
We see so many patterns around us in our daily life. We know that a pattern is an arrangement of objects, colors, or numbers placed in a certain order. Some patterns neither grow nor reduce but only r… -
Patterns in Math | Missing Number | Counting Numbers | Worksheets
Dec 13, 24 12:31 AM
Finding patterns in math is very important to understand the sequence in the series. We need to find the exact missing number that from the group of numbers. The counting numbers may be counting -
Concept of Pattern | Similar Patterns in Mathematics | Similar Pattern
Dec 12, 24 11:22 PM
Concept of pattern will help us to learn the basic number patterns and table patterns. Animals such as all cows, all lions, all dogs and all other animals have dissimilar features. All mangoes have si… -
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 12, 24 10:31 PM
2nd grade geometry worksheet -
Types of Lines |Straight Lines|Curved Lines|Horizontal Lines| Vertical
Dec 09, 24 10:39 PM
What are the different types of lines? There are two different kinds of lines. (i) Straight line and (ii) Curved line. There are three different types of straight lines. (i) Horizontal lines, (ii) Ver…
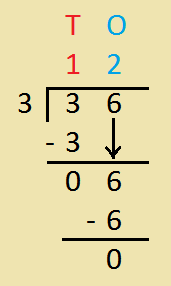
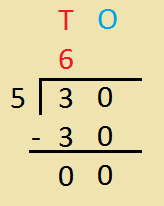
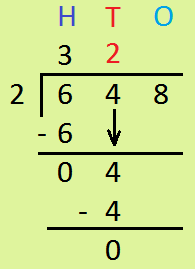
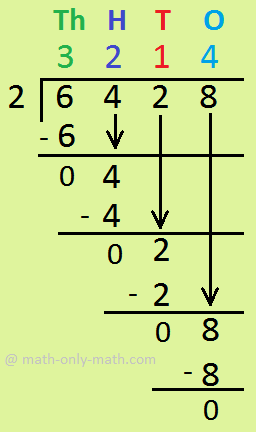
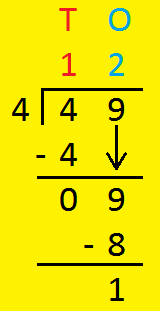
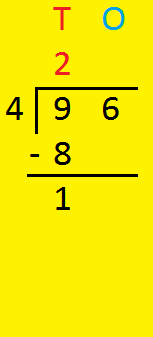
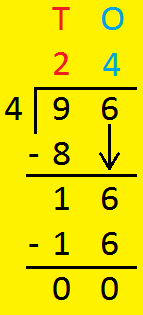
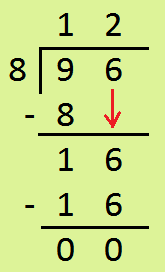
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.