Comparison of Numbers

In comparison of numbers we will learn to compare 4-digit numbers. The same rules are applied to compare numbers having more than 4 digits.

How to learn and understand comparison of numbers?

In everyday life, we always come across numbers and we often have to compare them and make a decision.

It would be depending on two things:

(a) Number of digits

(b) Place value of digits

Now, Let us learn how we can compare numbers.

Rules for Comparison of Numbers:

Rule I: We know that a number with more digits is always greater than the number with less number of digits.

Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits.

To learn and understand comparison of numbers the rules are generalized here:

Rule (1): The number/numeral having more digits is greater.

We know that a number with more digits is always greater than the number with less number of digits.

(i) The number of 2 digits is greater than the number of one digit.

(ii) The number of 3 digits is greater than the number having 2 or 1 digit.

(iii) The number of 4 digits is greater than 3 or 2 or 1 digit number.

(iv) 5-digit number > 4-digit number > 3-digit number ………… etc.

(v) 6-digit number > 5-digit number > 4-digit number ………… etc.

As:

     10 > 9;

     35 > 8;

     100 > 99 > 9;

     124 > 35;

     239 > 98;

     1250 > 998;

     1291 > 948;

     23051 > 8735;

     24,692 > 4,600

     351246 > 92835 > 5298 > 376 > 93.

Example:

Which is greater?

(i) 20,36,15,589 or 6,59,76,456

(ii) 40,201 or 4,999

(iii) 1,29,081 or 90,281

Solution:

(i) 20,36,15,589 or 6,59,76,456

The number 20,36,15,589 has 9-digits and 6,59,76,456 has 8-digits.

So, 20,36,15,589 > 6,59,76,456

(ii) 40,201 or 4,999

40,201 has 5 digits and 4,999 has 4 digits.

So, 40,201 > 4,999

(iii) 1,29,081 or 90,281

1,29,081 has 6 digits and 90,281 has 5 digits.

So, 1,29,081 > 90,281

Rule (2): (a) If two numbers have the same number of digits, we compare them on the basis of their extreme left digits. The number with the greater extreme left digit is greater.

As:

(i) 514 > 298, because 5 > 2

(ii) 6138 > 5978, because 6 > 5

(iii) 32516 > 19768, because 3 > 1

(iv) 451926 > 351658, because 4 > 3

(b) If the extreme left digits of two numbers are the same, we compare them on the basis of the next digits towards their right and so on.

As:

(i) 64283 > 63198, because 6 = 6, but 4 > 3

(ii) 24567 > 22381, because 2 = 2, but 4 > 2

(iii) 83,643 > 83,449, because 83 = 83, but 6 > 4

(iv) 367825 > 367543, because 367 = 367, but 8 > 5

In other words;

When the two numbers have the same number of digits, we start comparing the digits from the left most place until we come across unequal digits.

For example:

Compare 29,384 and 20,364

Both numbers are 5-digit numbers.

Let us compare the digits in left most place, we find that both numbers have same digit. Next, we compare the digits in the second most left place, we find that 9> 0.

So, 29,384 > 20,364

These are the rules to teach comparison of numbers. Parents and teachers can also follow these rules to teach the students how to compare  numbers.

Follow the below link to understand the examples on comparison of numbers.

Solved Examples of Comparison of Numbers:

A number having the greater number of digits is the greater number.

1. Compare 69,56,16,430 and 69,37,82,890

Solution:

Both numbers have same numbers of digits.

Let us compare the digits in the left most place, we find the both numbers have same digits in ten-crores and crores place. Next, we compare the digits at ten-lakhs place. Here 5 > 3.

Thus, 69,56,16,430 > 69,37,82,890.

2. Compare: 

(a) 8 and 12. 

8 is a single digit number. 12 has two digits. 

8 < 12

(b) 1342 and 342

The number of digits in 1342 is greater than the number of digits in 342.

1342 > 342

If two numbers have the same number of digits, then line up the digits according to place value. Compare the digits beginning with the greatest place. 

3. Compare: 

(a) 5869 and 4369

5 > 4

So, 5869 > 4369

(b) 74186 and 74586

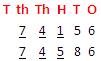
7 = 7

4 = 4

1 < 5

So, 74586 > 74186

When two numbers have different numbers of digits the number with the greater number of digits will be the greater:

4. Which is the greater?

(i) 5,12,964 or 291 (ii) 1,56,201 or 27,193

Solution:

(i) 5,12,964 has 6 digits and 291 has 3 digits.

So, 5,12,964 is greater than 291 or ,12,964 > 291

(ii) 1,56,201 has 6 digits and 27,193 has 5 digits.

So, 1,56,201 is greater than 27,193 or 1,56,201 > 27,193

When the two numbers have the same number of digits: In this case, we proceed as follows:

Step I: First compare the digits at the left-most place in both the numbers. If they are not equal then the number which has the greater digit at this place is greater than the other.

Step II: If they are equal, then compare the second digits from left in both the numbers. If they are not equal then the number which has the greater digit at this place is greater than the other.

Step III: If they are equal in value, we compare their third digits from the left. Continue this process until we come across unequal digits at the corresponding places.

5. Compare:

(i) 35,306 and 35,419

(ii) 7,34,510 and 7,34,578

(i) Consider 35,306 and 35,419. Both are 5-digit numbers.

We start from the left-most digits. Here, 3 = 3.

Next, we compare the second digits from the left. Here, 5 = 5.

Next, we compare the third digits from the left. Here, 3 < 4

Thus, 35,306 < 35,419 or 35,419 > 35,306.

(ii) Consider 7,34,510 and 7,34,578. Both are 6-digit numbers.

Comparing the digits, we have

7 = 7 (left-most digits)

3 = 3 (second digits from the left)

4 = 4 (third digits from the left)

5 = 5 (fourth digits from the left)

1 < 7 (fifth digits from the left)

Thus, 7,34,510 < 7,34,578 or 7,34,578 > 7,34,510.

Ordering of Large Numbers

The numeral with more digits represents the greater number.

For example:

(i) 5,643 > 342

(ii) 11,896 < 121,543

To compare two numbers having the same number of digits we start comparing from the leftmost digit.

How we order the large numbers to compare one number with another number?

6. Compare 19,528 and 25,364

Compare the digits in the ten thousands place.

Since, 1 < 2

19528 < 25364

7. Compare 85,461 and 83,989

Both the numbers have 8 in the ten thousands place.

Therefore, compare the digits in the thousands place.

5 > 3

Therefore, 85,461 > 83,989

8. Compare 6,34,582 and 6,39,285

Both the numbers have 6 in the lakhs place and 3 in the ten thousands place.

So, compare the digits in the thousands place.

4 < 9

Therefore, 6,34,582 < 6,39,285

9. Form the smallest and biggest six digit numbers using the digits 3, 1, 5, 8, 7, 4

Arrange the digits in ascending order.

1, 3, 4, 5, 7, 8

Therefore, the smallest number is 1,34,578.

Arrange the digits in descending order.

8, 7, 5, 4, 3, 1

Therefore, the biggest number is 8,75,431.

Questions and Answers on Comparison of Numbers:

A. How to compare two different digits numbers?

Working Rules for compare two different digit numbers are:

Step I: Count the total number of digits in each number.

Step II: The number having more number of digits is the greater one.

Step III: The number having less number of digits is the smaller one

1. Which one is greater, 9752 or 25701?

Solution:

Step I: Number of digits in 9752 is 4. Number of digits in 25701 is 5.

Step II: Since the no. of digits in the number 25701 is more than that in 9732 therefore, 25701 is greater than 9752.

2. Which one is smaller, 257 or 2570?

Solution:

Step I: No. of digits in 257 is 3 and no. of digits in 2570 is 4.

Step II: Since the no, of digits in the number 257 is less than that in 2570, therefore, 257 is smaller than 2570.

3. Which one is the greatest, 657 or 2859 or 13992?

Solution:

Step I: Number of digits in 657 is 3. Number of digits in 2859 is 4 Number of digits in 13992 is 5.

Step II: Since the no. of digits in the number 13992 is more than that in 657 and 2859 therefore, 13992 is the greatest of all.

4. Compare 75083 and 134028.

Solution:

Here 75083 has five digits while 134028 has six digits.

We know that number having more digits is greater.

Therefore, 134028 > 75083

B. How to compare two numbers when number of digits are same?

Step I: Compare the leftmost digits in the two numbers.

Step II: The number with the greater leftmost digit is greater.

Step III: In case, the leftmost digits are the same, compare the next left digits in both the numbers.

Step IV: The number with the greater digit is greater.

Step V: In case these digits are also the same, repeat step 3 and step 4 till you get the answer.

1. Which one is greater, 9836 or 9859?

Solution: 

Step I: Leftmost digits are the same, i.e., 9 = 9

Step II: Next left digits are also the same. i.e., 8 = 8

Step III: The next left digit 3 in 9836 is less than the corresponding left digit Sin 9859.

Therefore, 9859 is greater than 9836.

2. Which one is smaller, 1482 or 1471 ?

Solution:

Since 8 is greater than 7, so 1471 is smaller than 1482.

3. Which is greater: 96428 or 96728 ?

Solution:

Here both the numbers have five digits.

Ten thousands place and thousands place both the numbers have same digits.

At hundred place the first number is 4 while the second number is 7.

We know that 7 > 4.

Hence, 96728 > 96428.

Worksheet on Comparing and Ordering Numbers:

I. Put the right sign (<, > or =)

(i) 6,397                …………              6,937

(ii) 27,839              …………            25,899

(iii) 32,590              …………            62,890

(iv) 4,15,296           …………          4,27,866

(v) 6,32,700            …………          6,32,200

(vi) 3,20,065            …………         3,20,065

Answers:

I. (i) <

(ii) >

(iii) <

(iv) <

(v) >

(vi) =

II. Compare the numbers given below. Put > or < in the box.

(i) 384926             ...........                 348962

(ii) 795642            ...........                 759642

(iii) 562186           ...........                 561286

(iv) 99909             ...........                 99990

Answer:

II. (i) >

(ii) >

(iii) >

(iv) <

III. Fill in the blank using >, = or <:

(i) 2,63,149 _____ 5,92,500

(ii) 6,54,738 _____ 6,54,295

(iii) 4,651 _____ 79,514

(iv) 2,506 _____ 289

(v) 7,53,693 _____ 1,23,009

(vi) 66,329 _____  9,51,780

(vii) 6,29,103 _____ 4,51,633

(viii) 1,520 _____ 624

(ix) 9,16,358 _____ 9,16,358

(x) 6,85,196 _____ 8,65,209

(xi) 95,163 _____ 6,510

(xii) 2,50,693 _____ 2,56,094

(xiii) 37,541 _____ 37,541

(xiv) 5,50,084 _____ 30,508

Answer:

III. (i) <

(ii) >

(iii) <

(iv) >

(v) >

(vi) <

(vii) >

(viii) >

(ix) =

(x) <

(xi) >

(xii) <

(xiii) =

(xiv) >

IV. Circle the right answer.

A. The greatest number among the given is:

(i) 89,306                    (ii) 8,09,306                    (iii) 8,09,606

B. The smallest number among the given is:

(i) 1,28,075                    (ii) 2,18,057                   (iii) 1,39,075

C. I want to buy a car with least price. Which one should I buy?

(i) $5,47,800                   (ii) $4,99,900                 (iii) 6,01,800

D. Given below is the population of 3 cities. The most populous city is:

(i) City A - 8,77,310        (ii) City B - 7,92,600       (iii) City C - 5,98,200

E. Given below is the distance of 3 towns from New York. The closest town is

(i) Town A - 8,65,015 m    (ii) Town B - 8,65,880 m   (iii) Town C - 8,70,009 m

Answers:

IV. A. (iii)

B. (i)

C. (ii)

D. (i)

E. (i)

V. Find the largest number in each group:

(i) 8,39,216; 8,93,162; 2,16,893; 6,89,312.

(ii) 3,70,621; 2,06,713; 6,30,271; 3,60,217.

(iii) 19,754; 45,791; 95,714; 71,459.

(iv) 5,320; 3,520; 2,530; 2,053.

Answer:

V. (i) 8,93,162

(ii) 6,30,271

(iii) 95,714

(iv) 5,320

VI. Find the smallest number in each group:

(i) 6,09,268; 6,90,286; 8,60,268; 6,90,624.

(ii) 2,51,673; 4,51,637; 3,51,768; 2,51,366.

(iii) 8,81,750; 8,91,750; 9,18,750; 8,18,570.

(iv) 47,30,172; 4,70,312; 4,07,312; 7,40,312.

Answer:

VI. (i) 6,09,268

(ii) 2,51,366

(iii) 8,18,570

(iv) 4,07,312

VII. Comparison of Large Number

      Insert >, < or = in the boxes as required.

(i) 4,020,000,000   ⯀  24,30,20,432

(ii) 17,36,21,209    ⯀  320,248,342

(iii) 17,120,136,104  ⯀  94,24,97,596

(iv) 40,32,17,546    ⯀  2,107,318,217

Answer:

VII. (i) >

(ii) <

(iii) >

(iv) <

Related Concept 

• Formation of Numbers.
• Finding Out the Numbers
• Names of the Numbers.
  
• Numbers Showing on Spike Abacus.
  
• 1 Digit Number on Spike Abacus.
  
• 2 Digits Number on Spike Abacus.
  
• 3 Digits Number on Spike Abacus.
  
• 4 Digits Number on Spike Abacus.
  
• 5 Digits Number on Spike Abacus.
  
• Large Number.
• Place Value Chart.
• Place Value.
• Problems Related to Place Value.
• Expanded form of a Number.
• Standard Form.
• Comparison of Numbers.
• Example on Comparison of Numbers.
• Successor and Predecessor of a Whole Number.
  
• Arranging Numbers.
  
• Formation of Numbers with the Given Digits.
• Formation of Greatest and Smallest Numbers.
• Examples on the Formation of Greatest and the Smallest Number.
• Rounding off Numbers.

4th Grade Math Activities

From Comparison of Numbers to HOME PAGE