Rounding off Numbers

Rounding off numbers are discussed here, where we need to round a number. Rounding can be done for every place value of a number.

(i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left.

(ii) If we purchase another thing and its cost is $15.78. The cost is rounded up to its nearest $16. 0.22 or 22¢ more is taken.

Similarly, any number is taken to its nearest convenient whole number. As 48 is nearer to 50 than 40, so 48 may be rounded up to 50. This is called rounding off the number. In the process of rounding of a number, it is taken to its closest whole number.

Rounding off a number makes it easier to estimate the answer in our daily life. It is also an easy way to check calculations mentally. Look at the number line below and observe how rounding of a number can be done using the number-line.

11 is closer to 10 than 20. Hence 11 is rounded down to 10. 28 is closer to 30 than 20. Hence 28 is rounded up to 30.

If the given number is between the two multiples of ten, it is rounded up to the higher multiple. So 5 is rounded up to 10.

Note: To round off a number to the nearest tens, we round off it to the nearest multiple of ten.

Let us understand the concept of estimations taking examples from our everyday life.

• How many students are there in class IV? There are around 2000 students in class IV

• What is the distance between your school and home? My school is about 5 km away from my home.

Both the answers above are not exact. In both the cases the answers are rounded off Rounding off a number doesn't give the exact value but a value close to the answer.

Michael, the stationer, had noted the number of pencils and erasers in his shop. But he had lost the note. He remembers that there were about 50 pencils and 60 erasers.

The numbers 50 and 60 are close to the exact numbers.

These numbers are said to be rounded off.

Later, Michael found the note.

There were exactly 47 pencils and 62 eraser in his shop.

1. 47 is between 40 and 50.

But 47 is more closer to 50 than 40.

So, 47 is rounded off to 50.

2. 62 is between 60 and 70.

But 62 is more closer to 60 than 70.

So, 62 is rounded off to 60.

Remember

• A number is rounded Down to the nearest ten if the ones digit is 4 or less.

• A number is rounded Up to the nearest ten if the ones digit is 5 or more.

Consider the following examples:

Round off a Number to the Nearest Tens:

1. Round 78 to the nearest multiple of 10.

Solution:

To round off a number to the nearest tens, we round off it to the nearest multiple of ten.

78 is situated between 70 and 80. The middle of 70 and 80 is 75. 78 is nearer to 80 and farther from 70. 

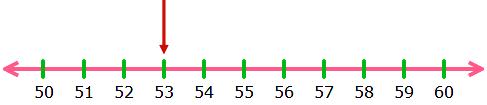
2. Round 53 to its nearest multiple of 10.

Solution:

53 is situated between 50 and 60. The middle number between 50 and 60 is 55.

53 is before 55, so it is rounded down to 50.

(When any number is situated half way or in the middle of two convenient whole numbers, it is rounded up to the higher whole number)

55 is rounded up to 60, 75 is rounded up to 80

54 is rounded down to 50, 74 is rounded down to 70

3. 37 is rounded up to 40 because 37 is closer to 40 than 30.

Round off a Number to the Nearest Hundreds:

To round off a number to the nearest hundreds, we round off it to the nearest multiple of hundred.

For Example:

225 is nearer to 200 than 300. So, 225 is rounded down to 200.

Round off Number to the Nearest Thousands:

To round off number to the nearest thousands, we round off it to the nearest multiple of thousand.

For example:

5431 is nearer to 5000 than 6000. So, 5431 is rounded down to 5000.

Solved Examples on Rounding off Numbers:

1. Round off 48 to the nearest 10.

Solution:

48 lies between 40 and 50.

48 is close to 50. so it can be rounded up to 50.

2. Round off 607 to the nearest 100.

Solution:

607 is close to 600, so it can be rounded down to 600.

3. Round off 1525 to this nearest 1000.

Solution:

1525 is close to 2000, so it can be rounded up to 2000.

4. Round off 42,873 to the nearest 10,000.

Solution:

42, 873 lies between 40,000 and 50,000, 42,873 is close to 40,000, so it can be rounded down to 40.000.

5. Round off 8741 to the nearest 100.

Solution:

8741 lies between 8700 and 8800.

8741 is close to 8700, so it can be rounded down to 8700.

6. Round off 72,519 to the nearest 1000.

Solution:

72,519 lies between 72,000 and 73,000.

72,519 is close to 73,000, so it can be rounded to 73,000.

Worksheet on Rounding off Numbers:

I. Round off the following numbers to nearest tens:

(i) 39

(ii) 183    

(iii) 102

(iv) 209

(v) 1268

(vi) 5186

(vii) 9549

(viii) 8911

Answers:

(i) 40

(ii) 180    

(iii) 100

(iv) 210

(v) 127068

(vi) 5190

(vii) 9550

(viii) 8910

II. Round off the following numbers to nearest hundreds:

(i) 3081

(ii) 5232

(iii) 4884

(iv) 6012

Answers:

(i) 3100

(ii) 5200

(iii) 4900

(iv) 6000

III. Round off the following numbers to nearest thousands:

(i) 4128

(ii) 2854

(iii) 14585

(iv) 27102

Answers:

(i) 4000

(ii) 3000

(iii) 15000

(iv) 27000

IV. Using number line, round off following numbers to the nearest tens:

(i) Round 72 to the nearest tens. 

72 is closer to _______. Hence it is rounded down to _______.

(ii) Round 39 to the nearest tens.

39 is closer to _______. Hence it is rounded down to _______.

Answer:

IV. (i) 72 is closer to 70. Hence it is rounded down to 70.

(ii) 39 is closer to 40. Hence it is rounded up to 40.

V. Round the given numbers to the nearest tens:

(i) 42

(ii) 67

(iii) 89

(iv) 47

(v) 56

(vi) 78

Answer:

V. (i) 40

(ii) 70

(iii) 90

(iv) 50

(v) 60

(vi) 80

VI. Round off the following numbers to the nearest 10.

(i) 73

(ii) 96

(iii) 28

(iv) 65

(v) 101

(vi) 234

(vii) 791

(viii) 552

(ix) 2,532

(x) 6,103

(xi) 8,354

(xii) 5161

(xiii) 50,217

(xiv) 63,482

(xv) 25,000

(xvi) 72,093

(xvii) 3,27,816

(xviii) 4,56,763

(xix) 4,51,760

(xx) 6,34,179

Answer:

VI. (i) 70

(ii) 100

(iii) 30

(iv) 70

(v) 100

(vi) 230

(vii) 790

(viii) 550

(ix) 2,530

(x) 6,100

(xi) 8,350

(xii) 5,160

(xiii) 50,220

(xiv) 63,480

(xv) 25,000

(xvi) 72,090

(xvii) 3,27,820

(xviii) 4,56,760

(xix) 4,51,760

(xx) 6,34,180

VII. Round off the following numbers to the nearest 100.

(i) 450

(ii) 580

(iii) 190

(iv) 630

(v) 2,413

(vi) 5,628

(vii) 9,810

(viii) 3,683

(ix) 62,018

(x) 74,560

(xi) 41,820

(xii) 28,316

(xiii) 8,22,210

(xiv) 9,30,000

(xv) 7,41,217

(xvi) 9,69,251

Answer:

VII. (i) 500

(ii) 600

(iii) 200

(iv) 600

(v) 2,400

(vi) 5,600

(vii) 9,800

(viii) 3,700

(ix) 62,000

(x) 74,600

(xi) 41,800

(xii) 28,300

(xiii) 8,22,200

(xiv) 9,30,000

(xv) 7,41,200

(xvi) 9,69,300

VIII. Round off the following numbers to the nearest 1000.

(i) 7,856

(ii) 1,520

(iii) 8,345

(iv) 2,138

(v) 12,340

(vi) 43,200

(vii) 71,272

(viii) 84,000

Answer:

VIII. (i) 8,000

(ii) 2,000

(iii) 8,000

(iv) 2,000

(v) 12,000

(vi) 43,000

(vii) 71,000

(viii) 84,000

IX. State true of false.

(i) 519 rounded off to the nearest 10 is 510.

(ii) 2,195 rounded off to the nearest 1000 is 3000.

(iii) 85,000 rounded off to the nearest 1000 is 85,000.

(iv) 76,715 rounded off to the nearest 100 is 77,000.

Answer:

IX. (i) False

(ii) False

(iii) True

(iv) False

X. Here are the attendance figures for 5 cricket matches. Round each figure the nearest 1000, 100 and 10.

Answer:

X. (i) 6000; 5700, 5720

(ii) 7000; 6900; 6910

(iii) 8000, 8000, 8000

(iv) 8000, 8500, 8500

Related Concept

● Formation of Numbers.

● Finding Out the Numbers

● Names of the Numbers.

● Numbers Showing on Spike Abacus.

● 1 Digit Number on Spike Abacus.

● 2 Digits Number on Spike Abacus.

● 3 Digits Number on Spike Abacus.

● 4 Digits Number on Spike Abacus.

● 5 Digits Number on Spike Abacus.

● Large Number.

● Place Value Chart.

● Place Value.

● Problems Related to Place Value.

● Expanded form of a Number.

● Standard Form.

● Comparison of Numbers.

● Example on Comparison of Numbers.

● Successor and Predecessor of a Whole Number.

● Arranging Numbers.

● Formation of Numbers with the Given Digits.

● Formation of Greatest and Smallest Numbers.

● Examples on the Formation of Greatest and the Smallest Number.

● Rounding off Numbers.

4th Grade Math Worksheets

From Rounding off Numbers to HOME PAGE