Multiply a Number by a
2-Digit Numbers
How to multiply a number by a 2-digit numbers?
We shall revise here to multiply 2-digit and 3-digit numbers by a
2-digit number (multiplier) as well as learn another procedure for the
multiplication of 3-digit, 4-digit, etc., numbers by a 2-digit
multiplier.
I. Example to multiply 2-digit numbers by a 2-digit numbers:
Multiply 63 by 14
Solution:
(i) First Method
63 x 14
= (60 + 3) × (10 + 4) 63 = 60 + 3 14 = 10 + 4
= (60 + 3) × 10 + (60 + 3) × 4
= (600 + 30) + (240 + 12)
= 630 + 252
= 882
or, 63 × 14 = (60 + 3) (10 + 4)
= (60 + 3) x 4 + (60 + 3) x l0
= (240 +12) + (600 + 30)
= 252 + 630
= 882
(ii) Second Method
|
|
(a) 4 × 3 ones = 12 ones
(b) 4 × 6 tens = 24 tens = 240 ones
(c) 1 ten × 3 ones = 3 tens = 30 ones
(d) 1 ten = 10 × 6 tens = 10 × 60 ones = 600 ones
|
(iii) Third Method
|
|
(a) 14 = (10 + 4)
(b) 63 × 4 = 252
(c) 63 × 10 = 630
|
(iv) Fourth Method
|
|
(a) 14 = 4 ones + 1 ten
(b) 63 × 4 ones = 252 ones
(c) 63 × 1 ten = 63 tens
(Generally the fourth method is adopted)
|
II. Example to multiply 3-digit numbers by a 2-digit numbers:
1. Multiply 456 x 43
Solution:
(i) First Method
|
|
(a) 43 = 3 + 40
(b) 456 × 3 = 1368
(c) 456 × 40 = 18240
|
Therefore, 456 × 43 = 19608
(ii) Second Method
|
|
(a) 43 = 3 ones + 4 tens
(b) 456 × 3 ones = 1368 ones
(c) 456 × 4 tens = 1824 tens
|
Hence, Product = 19608
2. Find the product of 165 and 45.
|
|
→ 40 + 5
Multiply by 5
Multiply by 40
Add the two products
|
Answer: 7290
3. Multiply 687 and 23.
Solution:
|
Step I: Arrange the numbers vertically.
Step II: Multiply 687 by 3 ones 687 × 3 = 2061 Step III: Multiply 687 by 2 tens 687 × 20 = 13740 Step IV: Add 2061 and 13740 2061 + 13740 = 15801
|
Hence, 687 × 23 = 15801
|
III. Example to multiply 4-digit numbers by a 2-digit numbers:
1. Multiply 3157 x 56
Solution:
(i) First Method
|
|
(a) 56 = 6 + 50
(b) 3157 × 6 = 18942
(c) 3157 × 50 = 157850
|
(ii) Second Method
|
|
(a) 56 = 6 ones + 5 tens
(b) 3157 × 6 ones = 18942 ones
(c) 3157 × 5 tens = 15785 tens
|
Hence, Product = 176792
2. Multiply: 1793 × 25
|
|
→ 20 + 5
Multiply by 5
Multiply by 20
|
Answer: 44825
Questions and Answers on Multiply a Number by a 2-Digit Number:
1. Multiplication of 2-Digit Numbers by 2-Digit Numbers by column method.
(i) 12 × 11 = __________
(ii) 24 × 35 = __________
(iii) 42 × 81 = __________
(iv) 17 × 46 = __________
(v) 44 × 59 = __________
(vi) 73 × 94 = __________
Answers:
(i) 132
(ii) 840
(iii) 3402
(iv) 782
(v) 2596
(vi) 6862
2. Multiplication of 3-Digit Numbers by 2-Digit Numbers by column method.
(i) 139 × 21 = __________
(ii) 256 × 33 = __________
(iii) 507 × 62 = __________
(iv) 780 × 53 = __________
(v) 864 × 74 = __________
(vi) 972 × 80 = __________
Answers:
(i) 2919
(ii) 8448
(iii) 31434
(iv) 41340
(v) 63936
(vi) 77760
3. Multiplication of 4-Digit Numbers by 2-Digit Numbers by column method.
(i) 1457 × 25 = __________
(ii) 1183 × 46 = __________
(iii) 3107 × 77 = __________
(iv) 4662 × 11 = __________
(v) 9381 × 36 = __________
(vi) 6500 × 25 = __________
Answers:
(i) 36425
(ii) 54418
(iii) 239239
(iv) 51282
(v) 337716
(vi) 162500
You might like these
-
The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number. For example, 9,99,99,999 is predecessor of 10,00,00,000 or we can also
-
In 4th grade division worksheet we will solve division by 2-digit numbers, division by 10 and 100, properties of division, estimation in division and word problems on division.
-
In worksheet on word problems on division, all grade students can practice the questions on word problems involving division. This exercise sheet on word problems on division can be practiced by the students to get more ideas to solve division problems.
-
In worksheet on estimating the quotient, all grade students can practice the questions on estimate the quotient. This exercise sheet on estimating quotient can be practiced by the students to get more ideas. Find the estimated quotient for the following divisions:
-
To estimate the quotient, we first round off the divisor and the dividend to the nearest tens, hundreds, or thousands and then divide the rounded numbers. In a division sum, when the divisor is made up of 2 digits or more than 2 digits, it helps if we first estimate the
-
Practice the questions given in the worksheet on divide by 10, 100 and 1000 divisors to find the quotient and remainder if any. Find the quotient and remainder (if any): I. Divide the given numbers by 10 and find the Quotient and Remainder. II. Divide the given numbers by
-
In worksheet on division by two-digit numbers, all grade students can practice the questions on dividing numbers by two digits numbers. This exercise sheet on dividing numbers can
-
In worksheet on division, all grade students can practice the questions to divide the numbers and find out the quotient and remainder. This exercise sheet on division can be practiced by the students to get more ideas to learn to divide and verify the results.
-
Division by 10 and 100 and 1000 are explained here step by step. when we divide a number by 10, the digit at ones place of the given number becomes the remainder and the digits at the remaining places of the number given the quotient.
-
In division by two-digit numbers we will practice dividing two, three, four and five digits by two-digit numbers. Consider the following examples on division by two-digit numbers: Let us use our knowledge of estimation to find the actual quotient. 1. Divide 94 by 12
-
In division we will see the relationship between the dividend, divisor, quotient and remainder. The number which we divide is called the dividend. The number by which we divide is called the divisor. The result obtained is called the quotient. The number left over is called
-
In 4th grade multiplication worksheet we will solve multiplication of 4-digit numbers, properties of multiplication, estimate the product and word problems on multiplication. I. Complete the given multiplication pyramids. First one is done for you. II. Fill in the blanks:
-
Word problems on multiplication for fourth grade students are solved here step by step. Problem Sums Involving Multiplication: 1. 24 folders each has 56 sheets of paper inside them. How many sheets of paper are there altogether? Solution: We can add 56 sheets 24 times
-
To estimate the product, we first round off the multiplier and the multiplicand to the nearest tens, hundreds, or thousands and then multiply the rounded numbers. Estimating products by rounding numbers to the nearest ten, hundred, thousand etc., we know how to estimate
-
In multiplication of a number by a 3-digit number are explained here step by step. Consider the following examples on multiplication of a number by a 3-digit number: 1. Find the product of 36 × 137
Related Concept
● Addition
● Word
Problems on Addition
● Subtraction
● Check
for Subtraction and Addition
● Word
Problems Involving Addition and Subtraction
● Estimating
Sums and Differences
● Find the
Missing Digits
● Multiplication
● Multiply
a Number by a 2-Digit Number
● Multiplication
of a Number by a 3-Digit Number
● Multiply a Number
● Estimating Products
● Word
Problems on Multiplication
● Multiplication
and Division
● Terms Used in
Division
● Division
of Two-Digit by a One-Digit Numbers
● Division
of Four-Digit by a One-Digit Numbers
● Division
by 10 and 100 and 1000
● Dividing Numbers
● Estimating
the Quotient
● Division
by Two-Digit Numbers
● Word
Problems on Division
4th Grade Math Activities
From Multiply a Number by a 2-Digit Number to HOME PAGE
Didn't find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
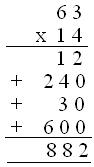
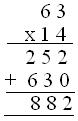
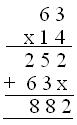
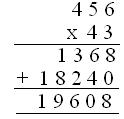
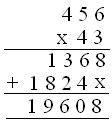
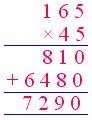
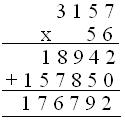
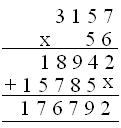
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.