4th Grade Addition Worksheet

In 4th grade addition worksheet we will solve addition of 4-digit numbers without regrouping, addition of 4-digit numbers with regrouping, addition of 5-digit numbers with regrouping and word problems on addition.

I. Add the given numbers:

(i) 3457 and 4522

(ii) 2583 and 6439

(iii) 1865 and 5131

(iv) 7008 and 2995

II. Arrange the following numbers in columns and add:

(i) 4,256; 1,543 and 3,098

(ii) 3,894; 4,093 and 1,954

III. What is 2805 more than 6412?

IV. Find the sum of the smallest 4-digit number and the smallest 3-digit number.

V. Choose the right answer:

1. When we add zero to any number, the answer is:

(i) 0

(ii) 10

(iii) Number itself

2. 3468 + 7856 is same as:

(i) 3468

(ii) 7856 + 3468

(iii) 7856

3. The successor of 7849 is:

(i) 7850

(ii) 7848

(iii) 7489

4. What is 1300 more than 5267?

(i) 7000

(ii) 6567

(iii) 6267

VI. Fill in the blanks:

(i) 1,350 + __________ = 8,754 + 1,350

(ii) 8,403 + __________ = 8,403 

(iii) 0 +  __________ = 9,351

VII. Choose the right answer and fill in the blank.

Adding 1 to a number gives ……………………… of the number.

(i) Predecessor

(ii) No change

(iii) Successor

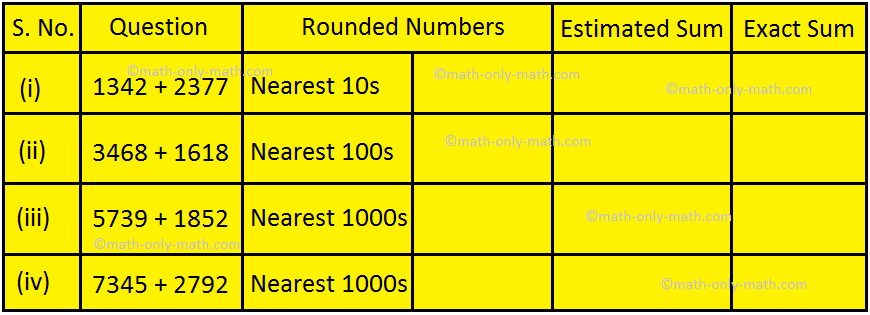
VIII. Estimate the given sums by rounding off the given numbers.

IX. In a week 3462 airplanes fly from the International airport in the morning and 2986 fly in the evening. How many total number of airplanes fly from the International airport in a week?

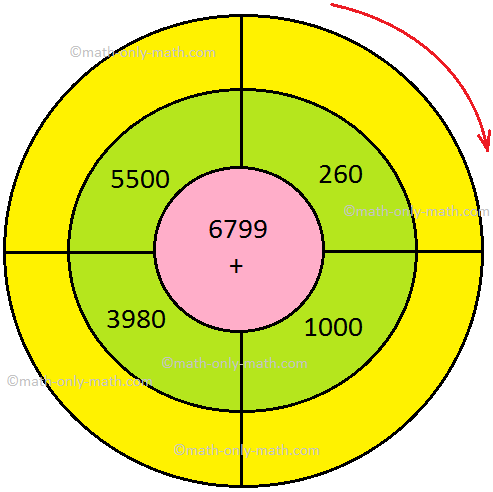
X. Given below is the addition wheel. Add the number of the inner circle with the number in the middle circle and write the answer in the outer circle.

XI. In a Marathon, Ron covered 3562 m and Shane is ahead of him by 628 m. How much distance has Shane covered?

XII. Choose the right answer:

1. 3988 + 4122 =

(i) 7000

(ii) 8110

(iii) 9000

2. The sum of smallest 4 digit number and largest 3 digit number is

(i) 9999

(ii) 1000

(iii) 1999

3. The successor of largest 4 digit number is

(i) 10000

(ii) 1000

(iii) 999

4. 348 + 1521 + 6131 =

(i) 7999

(ii) 8000

(iii) 8001

XIII. Write the next two numbers in the series:

(i) 2600, 3600, 4600, …………….., ……………..

(ii) 2450, 2500, 2550, …………….., ……………..

(iii) 35857, 36857, 378570, …………….., ……………..

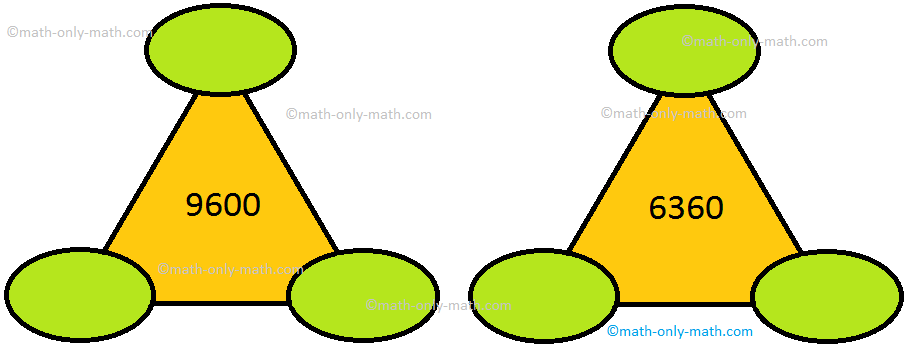
XIV. Write 3 same numbers in the circles of the triangle which add and give the sum equal to the number in the triangle.

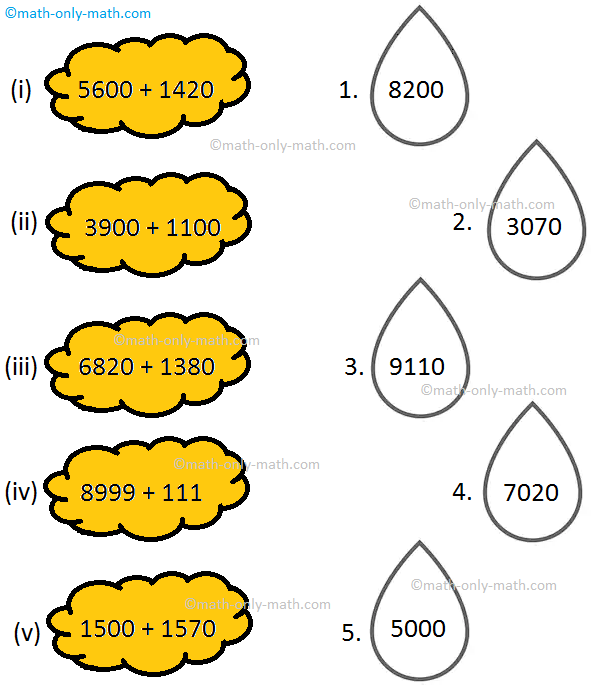
XV. Match the given sums to its solution by coloring the cloud and the rain drop with same color.

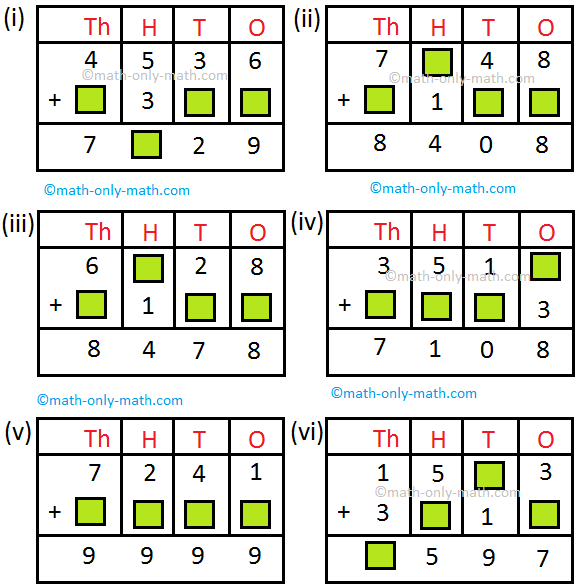
XVI. Find the missing numbers in the following:

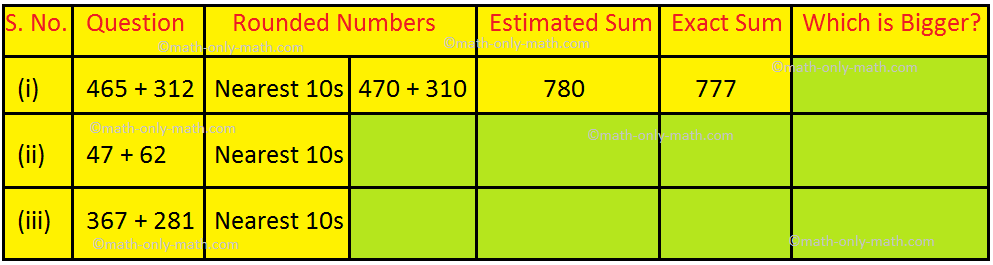
XVII. Find the estimated sum by rounding to the nearest 10s and compare with the exact sum.

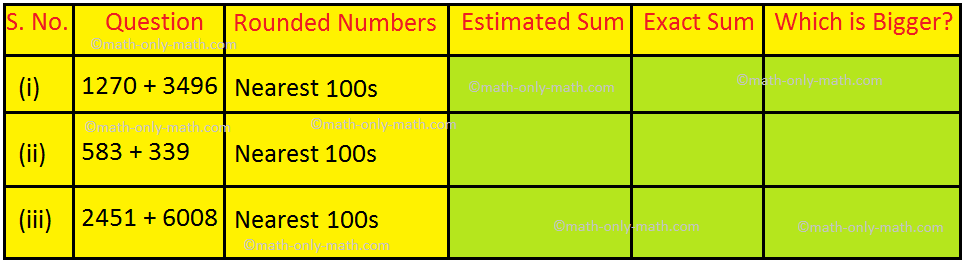
XVIII. Find the estimated sum by rounding to the nearest 100s and compare with the exact sum.

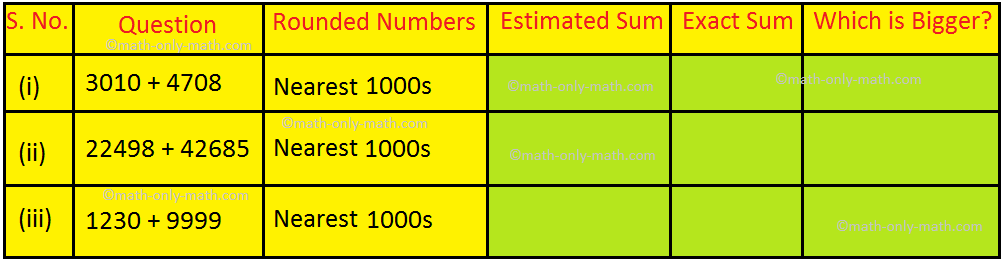
XIX. Find the estimated sum by rounding to the nearest 1000s and compare with the exact sum.

XX. In a school library, there are different types of books. Given below is the number of different types of books. Observe the data and answer the questions that follow.

(i) Arrange the books in the increasing order of their number.

(ii) What is the total number of books in the library. Give your answer to nearest 10 and 100.

(a) Nearest 10s

(b) Nearest 100s

(iii) If 1200 more Subject Reference Books are bought for the library, what will be the total number of reference books rounded to the nearest 10.

(iv) Compare the sum of Activity Books and Encyclopedia with the number of Subject Reference Books?

Word Problems on Addition:

XXI. Answer the following questions:

(i) At a meeting addressed by a leader, there were 3,285 men, 4,298 women and 1,275 children. How many people were present at the meeting?

(ii) Which number is 985 more than 6,732?

(iii) In an election, there were three candidates. The first candidate got 1975 votes, the second candidate got 4688 votes and the third candidate got 2149 votes. In all how many votes were polled?

(iv) In an examination 5,865 boys and 2,954 girls appeared. How many students in all appeared in the examination?

(v) A number is 468 more than 9268. Find the number.

XXII. The sum of 5 consecutive even members is 4520. What are the numbers?

Answers:

I. (i) 7979

(ii) 9022

(iii) 6996

(iv) 10003

II. (i) 8,897

(ii) 9,941

III. 9217

IV. 1100

V. 1. (iii) Number itself

2. (ii) 7856 + 3468

3. (i) 7850

4. (ii) 6567

VI. (iii) Successor

VII. (i) 8,754

(ii) 0

(iii) 9,351

VIII. (i) 1340 + 2380, 3720, 3719

(ii) 3500 + 1600, 5100, 5086

(iii) 6000 + 2000, 8000, 7591

(iv) 7000 + 3000, 10000, 10137

IX. 6448

X. 7059, 7799, 10779, 12299

XI. 4190 m

XII. 1. (ii)

2. (iii)

3. (i)

4. (ii)

XIII. (i) 5600, 6600

(ii) 2600, 2650

(iii) 38857, 39857

XIV. (i) 3200, 3200, 3200

(ii) 2120, 2120, 2120

XV. (i) 4

(ii) 5

(iii) 1

(iv) 3

(v) 2

XVI.

XVII. (i) estimated sum

(ii) 50 + 60, 110, 109, estimated sum

(iii) 370 + 280, 650, 648, estimated sum

XVIII. (i) 1300 + 3500 = 4800, 4767, estimated sum

(ii) 400 + 300 = 900, 922, Exact sum

(iii) 2500 + 6000 = 8500, 8459, estimated sum

XIX. (i) 3000 + 5000 = 8000, 7718, estimated sum

(ii) 22000 + 43000 = 65000, 65183, Exact sum

(iii) 1000 + 10000 = 11000, 11229, Exact sum

XX. (i) 2347, 3048, 6958, 8765

(ii) 21118, 21120, 21100

(iii) 22320

(iv) Number of subject reference books is greater

XXI. (i) 8858

(ii) 7717

(iii) 8812

(iv) 8819

(v) 9736

XXII. Let the 1st consecutive even member = 2x

Therefore, the 2nd consecutive even member = 2x + 2

The 3rd consecutive even member = 2x + 4

The 4th consecutive even member = 2x + 6

The 5th consecutive even member = 2x + 8

According to the problem, 

2x + (2x + 2) + (2x + 4) + (2x + 6) + (2x + 8) = 4520

⟹ 10x + 20 = 4520

⟹ 10x = 4520 - 20 

⟹ 10x = 4500

⟹ x = 4500/10

⟹ x = 450

Therefore, 1st consecutive even member = 2x = 2 × 450 = 900

The 2nd consecutive even member = 2x + 2 = 2 × 450 + 2 = 902

The 3rd consecutive even member = 2x + 4 = 2 × 450 + 4 = 904

The 4th consecutive even member = 2x + 6 = 2 × 450 + 6 = 906

The 5th consecutive even member = 2x + 8 = 2 × 450 + 2 = 908

Therefore, the numbers are 900, 902, 904, 906 and 908.

4th Grade Math Activities

4th Grade Math Worksheets

From 4th Grade Addition Worksheet to HOME PAGE