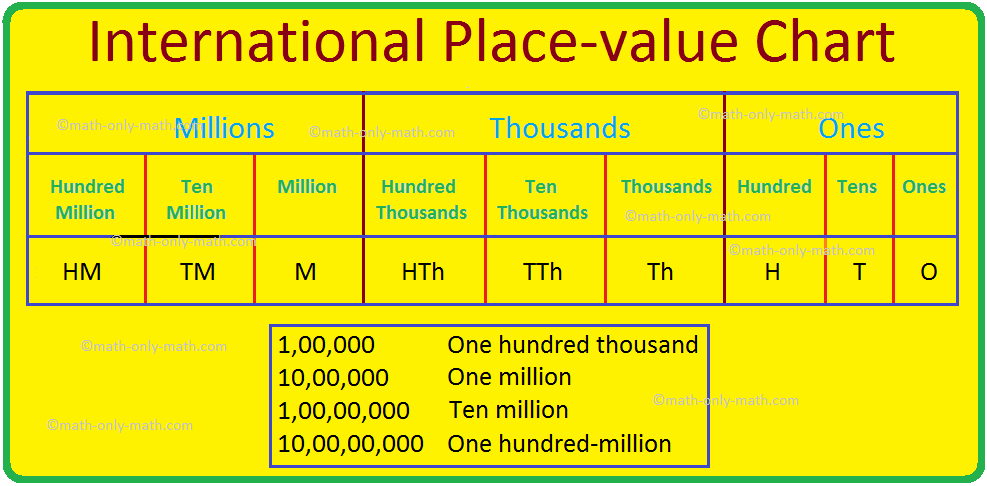
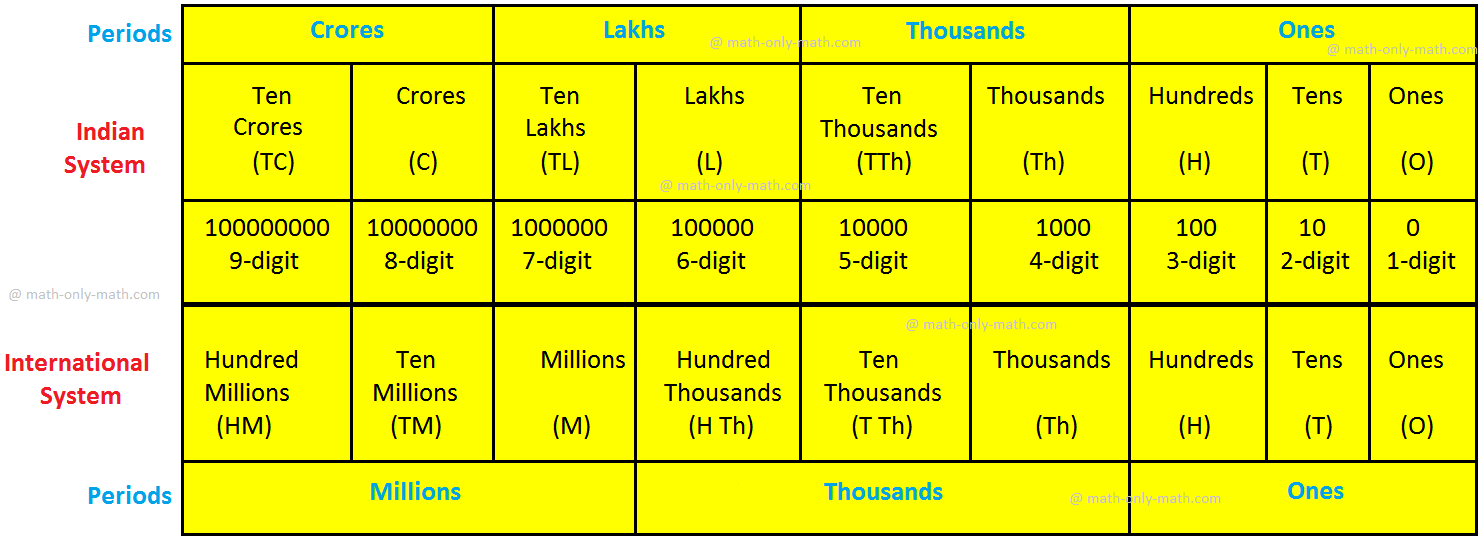
International Place-value Chart
In International place-value system, there are three periods namely Ones, thousands and millions for the nine places from right to left. Ones period is made up of three place-values. Ones, tens, and hundreds. The next period thousands is made up of one, ten and hundred-thousands. The next period thousands is made up of one, ten and hundred-thousands. The pattern continues and the next three places make millions period. So, writing a number in international place-value system, we insert commas after every three digits from the right.
To read the number, we read all the digits together in the same period followed by the name of the period from left to right.
|
Indian
Place-value Chart 1,00,000 One lakh 10,00,000 Ten lakh 1,00,00,000 One crore 10,00,00,000 Ten crore |
International Place-value Chart 1,00,000 One hundred thousand 10,00,000 One million 1,00,00,000 Ten million 10,00,00,000 One hundred-million |
Solved Examples on International Place-value Chart:
1. Place commas and name the following numbers using international place-value system.
(i) 62509842 (ii) 712984301
Solution:
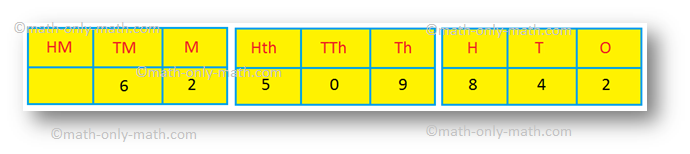
(i) 62509842
Let us arrange the digits in the place-value chart.
Sixty-two million, five hundred nine thousand, eight hundred forty-two.
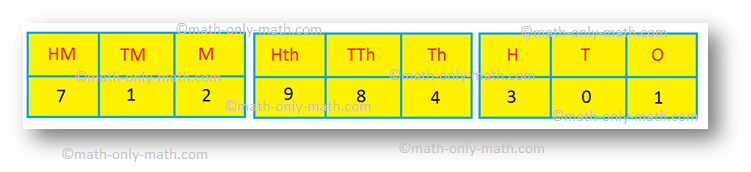
(ii) 712984301
Let us arrange the digits in the place-value chart.
Seven hundred twelve million, nine hundred eighty-four thousand, three hundred one.
2. Write the numeral 746504207 by inserting commas to separate periods in Indian and International system.
Solution:
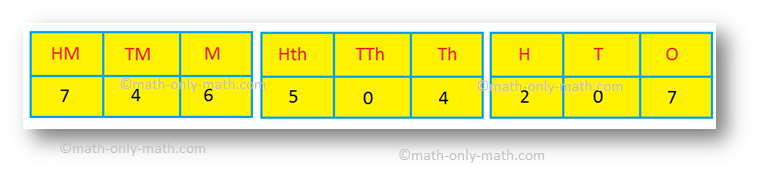
We enter each digit according to its place in the following Indian place-value chart.
The number is written as 74,65,04,207.
The number is read as seventy-four crore, sixty-five lakh, four thousand, two hundred seven.
We now enter each digit according to its place in the following International place-value chart.
The number is written as 746,504,207.
The number is read as seven hundred forty-six million, five hundred four thousand, two hundred seven.
3. Put the commas at the right place to change the numbers
given in Indian system to International system of numeration.
(i) 3,05,08,943
(ii) 2,28,86,073
(iii) 1,54,87,222
(iv) 7,75,92,000
(v) 81,80,32,622
Solution:
(i) 30,508,943
(ii) 22,886,073
(iii) 15,487,222
(iv) 77,592,000
(v) 818,032,622
4. Write the number for the given number names.
(i) Three million forty-five thousand six hundred fourteen: __________
(ii) Twenty-two million three hundred eighty-two thousand five hundred six: __________
(iii) Nine hundred four million five hundred twelve thousand six hundred forty: __________
(iv) Nine hundred ninety-nine million four hundred seventy-nine thousand three hundred ninety-two: __________
(v) One hundred million two thousand thirty: __________
Solution:
(i) 3,045,614
(ii) 22,382,506
(iii) 904,512,640
(iv) 999,479,392
(v) 100,002,030.
5. Complete the given table according to International system of numeration.
|
S.No. |
Numeral |
Number Name |
|
(i) |
37,824,500 | |
|
(ii) |
Two hundred thirty-six million four hundred fifty-two thousand seven hundred elevel. | |
|
(iii) |
585,893,057 | |
|
(iv) |
Two hundred twelve million two thousand twenty. | |
|
(v) |
980,089,090 |
Solution:
|
S.No. |
Numeral |
Number Name |
|
(i) |
37,824,500 |
Thirty seven million, eight hundred twenty-four thousand, five hundred. |
|
(ii) |
236,452,711 |
Two hundred thirty-six million four hundred fifty-two thousand seven hundred elevel. |
|
(iii) |
585,893,057 |
Five hundred eighty-five million, eight hundred ninety-three thousand, fifty-seven. |
|
(iv) |
212,002,020 |
Two hundred twelve million two thousand twenty. |
|
(v) |
980,089,090 |
Nine hundred eighty million, eighty-nine thousand, ninety. |
6. Form a number with:
2 at ten thousands place
0 at ten millions place
4 at thousands place
6 at ones place
7 at hundreds place
0 at tens place
8 at millions place
7 at hundred-millions place
7 at hundred-thousands place
Answer: 708,724,706
7. Form a number with:
5 at hundred-millions place
5 at ten-thousands place
6 at hundreds place
4 at ones place
0 at millions place
9 at tens place
1 at ten-millions place
2 at hundred-thousands place
0 at thousands place
Answer: 510,250,694
Indian System Vs. International System
There are two systems of place value chart, i.e., one is the Indian System of Numeration and the other is International System of Numeration.
Examples:
1. Compare the number names of 815253631, 925454723 and 533254328 by writing them in Indian System as well as International System of numeration.
Solution:
|
Indian System |
International System | |
|
(i) |
81,52,53,631 Eighty-one crore fifty-two lakh fifty-three thousand six hundred thirty-one |
815,253,631 Eight hundred fifteen million two hundred fifty-three thousand six hundred thirty-one. |
|
(ii) |
92,54,54,723 Ninety-two crore fifty-four lakh fifty-four thousand seven hundred twenty-three |
925,454,723 Nine hundred twenty five million four hundred fifty-four thousand seven hundred twenty-three |
|
(iii) |
53,32,54,328 Fifty-three crore thirty-two lakh fifty-four thousand three hundred twenty-eight |
533,254,328 Five hundred thirty-three million two hundred fifty-four thousand three hundred twenty-eight |
2. The difference between the place values of 8 in 718281579
(a) 8,000,000
(b) 7,920,000
(c) 80,000
(d) 800,000
Solution:
The given number is 718281579.
The place value of 8 in millions place = 8,000,000.
Place value of 8 in ten thousands place = 80,000.
Therefore, the difference between the place values of 8
= 8,000,000 - 80,000 = 7,920,000
Hence, the difference between the place values of 8 in 718281579 is 7,920,000.
So, the option (b) is correct, which is the required answer.
Worksheet on International Place-value Chart:
1. Convert the following International System into Indian System:
(1) 800,123,457
(ii) 73,254,263
(iii) 225,725,328
(iv) 620,917
(ν) 293,287,531
Answer:
1. (1) 80,01,23,457 →
Eighty crore one lakh twenty three thousand four hundred fifty seven.
(ii) 7,32,54,263 →
Seven crore thirty two lakh fifty four thousand two hundred sixty three.
(iii) 22,57,25,328 →
Twenty two crore fifty seven lakh twenty five thousand three hundred twenty eight.
(iv) 6,20,917 →
Six lakh twenty thousand nine hundred seventeen.
(ν) 29,32,87,531 →
Twenty nine crore thirty two lakh eighty seven thousand five hundred thirty one.
2. Find the difference between the place values of 9 in the following numbers:
(i) 90,469,881
(ii) 489,236,119
(iii) 3,949,562
(iv) 991,261,321
(ν) 580,986,912
Answer:
2. (i) 89,991,000
(ii) 8,999,991
(iii) 891,000
(iv) 810,000,000
(ν) 899,100
3. Write the following in the International System:
(i) 752003287
(ii) 12692852
(iii) 205008009
(iv) 92300813
(v) 150032872
Answer:
3. (i) 752,003,287 →
Seven hundred fifty two million three thousand two hundred eighty seven.
(ii) 12,692,852 →
Twelve million six hundred ninety two thousand eight hundred fifty two.
(iii) 205,008,009 →
Two hundred five million eight thousand nine
(iv) 92,300,813 →
Ninety two million three hundred thousand eight hundred thirteen.
(v) 150,032,872 →
One hundred fifty million thirty two thousand eight hundred seventy two.
4. Compare the number names of the following numbers by writing them in Indian System as well as International System of numeration:
(i) 315233729
(ii) 523549426
Answer:
4.
|
Indian System |
International System | |
|
(i) |
31,52,33,729 → Thirty one crore fifty two lakh thirty three thousand seven hundred twenty nine. |
315,233,729 → Three hundred fifteen million two hundred thirty three thousand seven hundred twenty nine. |
|
(ii) |
52,35,49,426 → Fifty two crore thirty five lakh forty nine thousand four hundred twenty six. |
523,549,426 → Five hundred twenty three million five hundred forty nine thousand four hundred twenty six. |
5. Choose the correct options.
The difference between the place values of 7 in 476,279,420 is
(a) 69,930,000
(b) 69,000,000
(c) 69,900,000
(d) 69,300,600
Answer:
5. (a) 69,930,000
You might like these
Roman Numerals | System of Numbers | Symbol of Roman Numerals |Numbers
How to read and write roman numerals? Hundreds of year ago, the Romans had a system of numbers which had only seven symbols. Each symbol had a different value and there was no symbol for 0. The symbol of Roman Numerals and their values are: Romans used different
Prime Triplet Numbers | Examples on Prime Triplet | Question Answer
A group of three consecutive prime numbers that differ by 2 is called a prime triplet. For example: (3,5,7) is the only prime triplet.
Find the Missing Digits | Missing Digits in Addition and Subtraction
How to find the missing digits in the blank spaces? Add the ONES: 5 + 9 = 14 Regroup as 1 Ten and 4 Ones Add the TENS: 2 + 1 carry over = 3 Write 2 in the box to make 3 + 2 = 5 Add the HUNDREDS: 4
Successor and Predecessor | Successor of a Whole Number | Predecessor
The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number. For example, 9,99,99,999 is predecessor of 10,00,00,000 or we can also
Formation of Greatest and Smallest Numbers | Arranging the Numbers
the greatest number is formed by arranging the given digits in descending order and the smallest number by arranging them in ascending order. The position of the digit at the extreme left of a number increases its place value. So the greatest digit should be placed at the
Arranging Numbers | Ascending Order | Descending Order |Compare Digits
We know, while arranging numbers from the smallest number to the largest number, then the numbers are arranged in ascending order. Vice-versa while arranging numbers from the largest number to the smallest number then the numbers are arranged in descending order.
Place Value | Place, Place Value and Face Value | Grouping the Digits
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know that the position of a digit in a number determines its corresponding value
Formation of Numbers with the Given Digits |Making Numbers with Digits
In formation of numbers with the given digits we may say that a number is an arranged group of digits. Numbers may be formed with or without the repetition of digits.
Addition & Subtraction Together |Combination of addition & subtraction
We will solve the different types of problems involving addition and subtraction together. To show the problem involving both addition and subtraction, we first group all the numbers with ‘+’ and ‘-‘ signs. We find the sum of the numbers with ‘+’ sign and similarly the sum
Worksheet on Roman Numerals |Roman Numerals|Symbols for Roman Numerals
Practice the worksheet on roman numerals or numbers. This sheet will encourage the students to practice about the symbols for roman numerals and their values. Write the number for the following: (a) VII (b) IX (c) XI (d) XIV (e) XIX (f) XXVII (g) XXIX (h) XII
Worksheet on Formation of Numbers | Questions on Formation of Numbers
In worksheet on formation of numbers, four grade students can practice the questions on formation of numbers without the repetition of the given digits. This sheet can be practiced by students
Comparison of Numbers | Compare Numbers Rules | Examples of Comparison
Rule I: We know that a number with more digits is always greater than the number with less number of digits. Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits. To learn
Worksheets on Comparison of Numbers | Find the Greatest Number
In worksheets on comparison of numbers students can practice the questions for fourth grade to compare numbers. This worksheet contains questions on numbers like to find the greatest number, arranging the numbers etc…. Find the greatest number:
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit number. I: Dividing 3-digit Number by 1-Digit Number without Remainder:
4th Grade Mental Math on Factors and Multiples |Worksheet with Answers
In 4th grade mental math on factors and multiples students can practice different questions on prime numbers, properties of prime numbers, factors, properties of factors, even numbers, odd numbers, prime numbers, composite numbers, tests for divisibility, prime factorization
Related Concept
- Formation of Numbers.
- Finding Out the Numbers
- Names of the Numbers.
- Numbers Showing on Spike Abacus.
- 1 Digit Number on Spike Abacus.
- 2 Digits Number on Spike Abacus.
- 3 Digits Number on Spike Abacus.
- 4 Digits Number on Spike Abacus.
- 5 Digits Number on Spike Abacus.
- Large Number.
- Place Value Chart.
- Place Value.
- Problems Related to Place Value.
- Expanded form of a Number.
- Standard Form.
- Comparison of Numbers.
- Example on Comparison of Numbers.
- Successor and Predecessor of a Whole Number.
- Arranging Numbers.
- Formation of Numbers with the Given Digits.
- Formation of Greatest and Smallest Numbers.
- Examples on the Formation of Greatest and the Smallest Number.
- Rounding off Numbers.
From International Place-value Chart to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Word Problems on Area and Perimeter | Free Worksheet with Answers
Jul 26, 24 04:58 PM
word problems on area and perimeter -
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 26, 24 04:37 PM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
Perimeter and Area of Irregular Figures | Solved Example Problems
Jul 26, 24 02:20 PM
Here we will get the ideas how to solve the problems on finding the perimeter and area of irregular figures. The figure PQRSTU is a hexagon. PS is a diagonal and QY, RO, TX and UZ are the respective d… -
Perimeter and Area of Plane Figures | Definition of Perimeter and Area
Jul 26, 24 11:50 AM
A plane figure is made of line segments or arcs of curves in a plane. It is a closed figure if the figure begins and ends at the same point. We are familiar with plane figures like squares, rectangles… -
5th Grade Math Problems | Table of Contents | Worksheets |Free Answers
Jul 26, 24 01:35 AM
In 5th grade math problems you will get all types of examples on different topics along with the solutions. Keeping in mind the mental level of child in Grade 5, every efforts has been made to introdu…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.