Subscribe to our YouTube channel for the latest videos, updates, and tips.
Expanded form of Decimal Fractions
We will discuss here about the expanded form of decimal fractions.
In expanded form of decimal fractions we will learn how to read and write the decimal numbers.
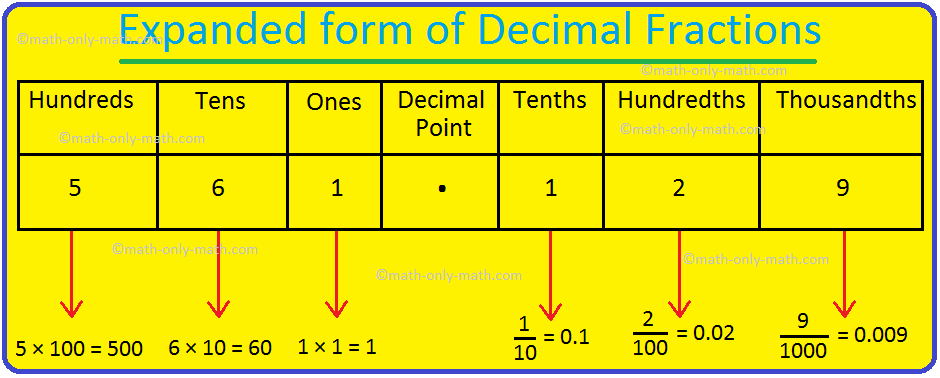
Decimal numbers can be expressed in expanded form using the place-value chart. Let us consider the number 561.129. Let us expand each of the digits using the place-value chart.
So, we can write 561.129 in the expanded form as follows.
561.129 = 500 + 60 + 1 + 0.1 + 0.02 + 0.009
= 5 hundreds + 6 tens + 1 ones + 1 tenths + 2 hundredths + 9 thousandths
= 500 + 60 + 1 + \(\frac{1}{10}\) + \(\frac{2}{100}\) + \(\frac{9}{1000}\)
Again,
493.2 = 4 hundreds + 9 tens + 3 ones + 2 tenths
= 400 + 90 + 3 + \(\frac{2}{10}\)
1436.74 = 1 thousands + 4 hundreds + 3 tens + 6 ones + 7 tenths + 4 hundredths
= 1000 + 400 + 30 + 6 + \(\frac{7}{10}\) + \(\frac{4}{100}\)
Note: When a decimal is missing either in the integral part or decimal part, substitute with 0.
Consider the number 123.437
Let us write the digits if this number as per their place value.
123.437 = 1 hundreds + 2 tens + 3 ones + 4 tenths + 3 hundredths + 7 thousandths
= 100 + 20 + 3 + 4/10 + 3/100 + 7/1000
= 100 + 20 + 3 + 0.4 + 0.03 + 0.007
Thus, 123.437 = 100 + 20 + 3 + 0.4 + 0.03 + 0.007
1. Write the decimal numbers in expanded
form:
(i) 3479.105
= 3 thousands + 4 hundreds + 7 tens + 9 ones + 1 tenths + 0 hundredths+ 5 thousandths
= 3000 + 400 + 70 + 9 + \(\frac{1}{10}\) + \(\frac{0}{100}\) + \(\frac{5}{1000}\)
(ii) 7833.45
= 7 thousands + 8 hundreds + 3 tens + 3 ones + 4 tenths + 5 hundredths
= 7000 + 800 + 30 + 3 + \(\frac{4}{10}\) + \(\frac{5}{100}\)
(iii) 21.1097
= 2 tens + 1 ones + 1 tenths + 0 hundredths + 9 thousandths + 7 ten thousandths
= 20 + 1 + \(\frac{1}{10}\) + \(\frac{0}{100}\) + \(\frac{9}{1000}\) + \(\frac{7}{10000}\)
(iv) 524.1
= 5 hundreds + 2 tens + 4 ones + 1 tenths
= 500 + 20 + 4 + \(\frac{1}{10}\)
(v) 143.011
= 1 hundreds + 4 tens + 3 ones + 0 tenths + 1 hundredths + 1 thousandths
= 100 + 40 + 3 + \(\frac{0}{10}\) + \(\frac{1}{100}\) + \(\frac{1}{1000}\)
(vi) 840.006
= 8 hundreds + 4 tens + 0 ones + 0 tenths + 0 hundredths + 6 thousandths
= 800 + 40 + 0 + \(\frac{0}{10}\) + \(\frac{0}{100}\) + \(\frac{6}{1000}\)
(vii) 64.21
= 6 tens + 4 ones + 2 tenths + 1 hundredths
= 60 + 4 + \(\frac{2}{10}\) + \(\frac{1}{100}\)
(viii) 4334.334
= 4 thousands + 3 hundreds + 3 tens + 4 ones + 3 tenths + 3 hundredths + 4 thousandths
= 4000 + 300 + 30 + 4 + \(\frac{3}{10}\) + \(\frac{3}{100}\) + \(\frac{4}{1000}\)
2. Write as decimal fractions:
(i) 8 thousands + 8 ones + 3 tenths + 9 hundredths
= 8008.39
(ii) 4000 + 7 + \(\frac{5}{10}\) + \(\frac{6}{100}\)
= 4007.56
(iii) 6 hundreds + 9 tens + 8 tenths + 4 thousandths
= 690.804
(iv) 3 tens + 7 ones + 6 hundredths + 8 thousandths
= 37.068
(v) 400 + 50 + 1 + \(\frac{9}{100}\)
= 451.09
(vi) 800 + 70 + 2 + \(\frac{8}{10}\) + \(\frac{5}{1000}\)
= 872.805
(vii) 6 tens + 5 tenths + 8 hundredths
= 60.58
(viii) 9 hundreds + 4 tens + 3 tenths + 4 hundredths
= 940.34
3. Write the following in short form.
(i) 100 + 0.5 + 0.06 + 0.008 (ii) 80 + 1 + 0.02 + 0.005
Solution:
(i) 100 + 0.5 + 0.06 + 0.008
= 100.568
(ii) 80 + 1 + 0.02 + 0.005
= 81.025
4. Write the place-value of the underlined digits.
(i) 2.47 (ii) 11.003 (iii) 5.175
Solution:
(i) 2.47
Place-value of 7 in 2.47 is 7 hundredths or 0.07.
(ii) 11.003
Place-value of 3 in 11.003 is 3 thousandths or 0.003.
(iii) 5.175
Place-value of 1 in 5.175 is 1 tenths or 0.1.
Expanded form of Decimals:
This is a form in which we add the place value of each digit forming the number.
Practice Problems on Expanded Form of Decimal Fractions:
I. Write each of the following decimals in expanded form:
(i) 38.54
(ii) 83.107
(iii) 627.074
Solution:
(i) 38.54 = 38 + \(\frac{5}{10}\) + \(\frac{4}{100}\) = 30 + 8 + 0.5 + 0.04
(ii) 83.107 = 83 + \(\frac{1}{10}\) + \(\frac{0}{100}\) + \(\frac{7}{1000}\)
= 80 + 3 + 0.1 + 0 + 0.007
= 80 + 3 + 0.1 + 0.007
(ii) 627.074 = 627 + \(\frac{0}{10}\) + \(\frac{7}{100}\) + \(\frac{4}{1000}\)
= 600 + 20 + 7 + 0 + 0.07 + 0.004
= 600 + 20 + 7 + 0.07 + 0.004
II. Write following in short form:
(i) 9 + \(\frac{3}{10}\) + \(\frac{4}{100}\)
(ii) 50 + 7 + \(\frac{6}{10}\) + \(\frac{2}{100}\) + \(\frac{4}{1000}\)
(iii) 100 + 4 + \(\frac{3}{10}\) + \(\frac{6}{1000}\)
Solution:
(i) 9 + \(\frac{3}{10}\) + \(\frac{4}{100}\) = 9.34
(β
±) 50 + 7 + \(\frac{6}{10}\) + \(\frac{2}{100}\) + \(\frac{4}{1000}\) = 57.624
(iii) 100 + 4 + \(\frac{3}{10}\) + \(\frac{6}{1000}\) = 104.306
Worksheet on Expanded form of Decimal Fractions
I. Write the given decimals in expanded form by fractional expansion.
One example has been done for you to get the idea how to do decimals in expanded form by fractional expansion.
1.73 = 1 + \(\frac{7}{10}\) + \(\frac{3}{100}\)
(i) 23.8
(ii) 60.27
(iii) 119.05
(iv) 276.207
Answers:
I. (i) 20 + 3 + \(\frac{8}{10}\)
(ii) 60 + 0 + \(\frac{2}{10}\) + \(\frac{7}{100}\)
(iii) 100 + 10 + 9 + 0 + \(\frac{5}{100}\)
(iv) 200 + 70 + 6 + \(\frac{2}{10}\) + 0 + \(\frac{7}{100}\)
II. Write the given decimals in expanded form by decimal expansion.
One example has been done for you to get the idea how to do decimals in expanded form by decimal expansion.
8.461 = 8 + 0.4 + 0.06 + 0.001
(i) 6.08
(ii) 36.505
(iii) 402.613
(iv) 700.037
Answers:
II. (i) 6 + 0.0 + 0.08
(ii) 30 + 6 + 0.5 + 0.00 + 0.005
(iii) 400 + 0 + 2 + 0.6 + 0.01 + 0.003
(iv) 700 + 0 + 0 + 0.0 + 0.03 + 0.007
III. Write the decimal number for the expansions given below.
(i) 10 + 6 + \(\frac{3}{10}\) + \(\frac{9}{1000}\)
(ii) 600 + 20 + 7 + \(\frac{1}{10}\) + \(\frac{3}{100}\) + \(\frac{7}{1000}\)
(iii) 2000 + 8 + \(\frac{3}{10}\) + \(\frac{9}{100}\)
(iv) 400 + 70 + 1 + 0.5 + 0.07 + 0.002
(v) 5000 + 80 + 0 + 0.2 + 0.002
Answers:
III. (i) 16.309
(ii) 627.137
(iii) 2008.39
(iv) 471.572
(v) 5080.202
IV. Write the following decimals in expanded form:
(i) 31.5
(ii) 37.53
(iii) 307.85
(iv) 752.34
(Ξ½) 882.146
(vi) 41.005
(vii) 345.083
(viii) 435.202
Answer:
IV. (i) 31.5 = 31 + 05
(ii) 37.53 = 30 + 7 + 0.5 + 0.03
(iii) 307.85 = 300 + 7 + 0.8 + 0.05
(iv) 752.34 = 700 + 50 + 2 + 0.3 + 0.04
(Ξ½) 882.146 = 800 + 80 + 2 + 0.1 + 0.04 + 0.006
(vi) 41.005 = 40 + 1 + 0.005
(vii) 345.083 = 300 + 40 + 5 + 0.08 + 0.003
(viii) 435.202 = 400 + 30 + 5 + 0.2 + 0.002
V. Write each of the following in decimal form:
(i) 9 + 4/10 + 6/100 + 2/1000
(ii) 600 + 40 + 5/1000
(iii) 300 + 3 + 5/10 + 2/1000
(iv) 700 + 40 + 7 + 2/100 + 3/1000
Answer:
V. (i) 9.462
(ii) 640.005
(iii) 303. 502
(iv) 747.023
VI. Fill in the boxes with correct numbers:
(i) 84.29 = 80 + π² + \(\frac{2}{10}\)+ \(\frac{9}{π²}\)
(ii) 35.265= 30 + 5 + \(\frac{π²}{10}\) + \(\frac{6}{100}\) + \(\frac{5}{π²}\)
(iii) 5672.053= 5000 + 600 + π² + π² + \(\frac{5}{π²}\) + \(\frac{3}{π²}\)
Answer:
VI. (i) 84.29 = 80 + 4 + \(\frac{2}{10}\) + \(\frac{9}{\mathbf{{\color{Red}100}}}\)
(ii) 35.265= 30 + 5 + \(\frac{\mathbf{{\color{Red}2}}}{10}\) + \(\frac{6}{100}\) + \(\frac{5}{\mathbf{{\color{Red}1000}}}\)
(iii) 5672.053= 5000 + 600 + 70 + 2 + \(\frac{5}{\mathbf{{\color{Red}100}}}\) + \(\frac{3}{\mathbf{{\color{Red}1000}}}\)
VII. Express in expanded form.
(i) 4.326
(ii) 29.629
(iii) 62.346
(iv) 28.429
(v) 82.031
(vi) 29.079
(vii) 97.458
(viii) 49.309
(ix) 318.073
(x) 518.318
(xi) 327.209
(xii) 214.342
(xiii) 617.829
(xiv) 970.079
(xv) 214.342
(xvi) 652.493
Answer:
VII. (i) 4 + 0.3 + 0.02 + 0.006
(ii) 20 + 9 + 0.6 + 0.02 + 0.009
(iii) 60 + 2 + 0.3 + 0.04 + 0.006
(iv) 20 + 8 + 0.4 + 0.02 + 0.009
(v) 80 + 2 + 0.0 + 0.03 + 0.001
(vi) 20 + 9 + 0.0 + 0.07 + 0.009
(vii) 90 + 7 + 0.4 + 0.05 + 0.008
(viii) 40 + 9 + 0.3 + 0.00 + 0.009
(ix) 300 + 10 + 8 + 0.0 + 0.07 + 0.003
(x) 500 + 10 + 8 + 0.3 + 0.01 + 0.008
(xi) 300 + 20 + 7 + 0.2 + 0.00 + 0.009
(xii) 200 + 10 + 4 + 0.3 + 0.04 + 0.002
(xiii) 600 + 10 + 7 + 0.8 + 0.02 + 0.009
(xiv) 900 + 70 + 0 + 0.0 + 0.07 + 0.009
(xv) 200 + 10 + 4 + 0.3 + 0.04 + 0.002
(xvi) 600 + 50 + 2 + 0.4 + 0.09 + 0.003
VIII. Write the following expanded form of decimals into short form of decimals / Express as decimals:
(i) 200 + 40 + 3 + 0.2 + 0.04 + 0.006
(ii) 100 + 60 + 5 + 0.3 +0.05 + 0.008
(iii) 60 + 6 + 0.7 + 0.08 + 0.009
(iv) 500 + 90 + 2 + 0.2 + 0.04 + 0.006
(v) 90 + 7 + 0.4 +0.01 + 0.007
(vi) 8 + 3/10 + 7/100 + 1/1000
(vii) 30 + 9 + 6/10 + 9/100 + 2/1000
(viii) 700 + 80 + 5 + 1/10 + 4/100 + 7/1000
Answer:
VIII. (i) 243.246
(ii) 165.358
(iii) 66.789
(iv) 592.246
(v) 97.417
(vi) 8.371
(vii) 39.692
(viii) 785.147
IX. Write in decimal form.
(i) 800 + 40 + 6 + 1/10 + 3/100 + 4/1000
(ii) 9000 + 60 + 9 + 3/100 + 7/1000
(iii) 6000 + 200 + 3 + 4/10 + 3/100 + 5/1000
(iv) 9000 + 60 + 9 + 7/100 + 3/1000
Answer:
IX. (i) 846.134
(ii) 9069.037
(iii) 6203.435
(iv) 9069.073
You might like these
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate
Word Problems on Decimals | Decimal Word Problems | Decimal Home Work
Word problems on decimals are solved here step by step. The product of two numbers is 42.63. If one number is 2.1, find the other. Solution: Product of two numbers = 42.63 One number = 2.1
Worksheet on Dividing Decimals | Huge Number of Decimal Division Prob
Practice the math questions given in the worksheet on dividing decimals. Divide the decimals to find the quotient, same like dividing whole numbers. This worksheet would be really good for the students to practice huge number of decimal division problems.
Worksheet on Multiplying Decimals | Product of the Two Decimal Numbers
Practice the math questions given in the worksheet on multiplying decimals. Multiply the decimals to find the product of the two decimal numbers, same like multiplying whole numbers.
Worksheet on Subtraction of Decimal Fractions | Subtracting Decimals
We will practice the questions given in the worksheet on subtraction of decimal fractions. While subtracting the decimal numbers convert them into like decimal then subtract as usual ignoring decimal point and then put the decimal point in the difference directly under the
Worksheet on Addition of Decimal Fractions | Word Problems on Decimals
We will practice the questions given in the worksheet on addition of decimal fractions. While adding the decimal numbers convert them into like decimal then add as usual ignoring decimal point and then put the decimal point in the sum directly under the decimal points of all
Ordering Decimals | Comparing Decimals | Ascending & Descending Order
In ordering decimals we will learn how to compare two or more decimals. (i) Convert each of them as like decimals. (ii) Compare these decimals just as we compare two whole numbers ignoring
Converting Fractions to Decimals | Solved Examples | Free Worksheet
In converting fractions to decimals, we know that decimals are fractions with denominators 10, 100, 1000 etc. In order to convert other fractions into decimals, we follow the following steps:
Multiplication of a Decimal by 10, 100, 1000 | Multiplying decimals
The working rule of multiplication of a decimal by 10, 100, 1000, etc... are: When the multiplier is 10, 100 or 1000, we move the decimal point to the right by as many places as number of zeroes after 1 in the multiplier.
Converting Decimals to Fractions | Solved Examples | Free Worksheet
In converting decimals to fractions, we know that a decimal can always be converted into a fraction by using the following steps: Step I: Obtain the decimal. Step II: Remove the decimal points from the given decimal and take as numerator.
How to Divide Decimals? | Dividing Decimals by Decimals | Examples
Dividing Decimals by Decimals I. Dividing a Decimal by a Whole Number: II. Dividing a Decimal by another Decimal: If the dividend and divisor are both decimal numbers, we multiply both the numbers by 10, 100, 1000, etc so that the divisor becomes a whole number
Division of a Decimal by a Decimal |Decimal Division|Dividing Decimals
Division of a decimal by a decimal are discussed here. 1. 14.7 Γ· 2.1 Solution: 14.7 Γ· 2.1 [Count the number of decimal digits in the divisor and we observe that after decimal there is 1
Dividing Decimals Word Problems Worksheet | Answers |Decimals Division
In dividing decimals word problems worksheet we will get different types of problems on decimals division word problems, dividing a decimal by a whole number, dividing a decimals and dividing a decimals by 10, 100 and 1000.
Multiplying Decimal by a Whole Number | Step-by-step Explanation|Video
Multiplying decimal by a whole number is just same like multiply as usual. How to multiply a decimal by a whole number? To multiply a decimal by a whole number follow the below steps
Multiplication of Decimal Numbers | Multiplying Decimals | Decimals
The rules of multiplying decimals are: (i) Take the two numbers as whole numbers (remove the decimal) and multiply. (ii) In the product, place the decimal point after leaving digits equal to the total number of decimal places in both numbers.
β Decimal.
Expanded form of Decimal Fractions.
Changing Unlike to Like Decimal Fractions.
Comparison of Decimal Fractions.
Conversion of a Decimal Fraction into a Fractional Number.
Conversion of Fractions to Decimals Numbers.
Addition of Decimal Fractions.
Problems on Addition of Decimal Fractions
Subtraction of Decimal Fractions.
Problems on Subtraction of Decimal Fractions
Multiplication of a Decimal Numbers.
Multiplication of a Decimal by a Decimal.
Properties of Multiplication of Decimal Numbers.
Problems on Multiplication of Decimal Fractions
Division of a Decimal by a Whole Number.
Division of Decimal Fractions by Multiples.
Division of a Decimal by a Decimal.
Division of a whole number by a Decimal.
Properties of Division of Decimal Numbers
Problems on Division of Decimal Fractions
Conversion of fraction to Decimal Fraction.
From Expanded form of Decimal Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Simple Interest | Word problem on Simple Interest | Free
Jun 19, 25 02:54 AM
In worksheet on simple interest we will get different types of question on calculating the simple interest, the principal amount, the rate of interest and the word problems on simple interest. -
Terms Related to Simple Interest | Simple Interest Formula | Principal
Jun 19, 25 12:20 AM
In terms related to simple interest we will learn all the terms related to simple interest. The terms related to simple interest are Interest, Principal, Amount, Simple Interest, Time or period of tim… -
Introduction to Simple Interest | Definition | Formula | Examples
Jun 18, 25 01:50 AM
In simple interest we will learn and identify about the terms like Principal, Time, Rate, Amount, etc. PRINCIPAL (P): The money you deposit or put in the bank is called the PRINCIPAL. -
5th Grade Profit and Loss Percentage Worksheet | Profit and Loss | Ans
Jun 18, 25 01:33 AM
In 5th grade profit and loss percentage worksheet you will get different types of problems on finding the profit or loss percentage when cost price and selling price are given, finding the selling pri… -
Worksheet on Profit and Loss | Word Problem on Profit and Loss | Math
Jun 18, 25 01:29 AM
In worksheet on profit and loss, we can see below there are some different types of questions which we can practice in our homework.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.