Division of a Decimal by a Whole Number
We will learn how to find the quotient in division of a decimal by a whole number.
To divide a decimal number by a whole number the division is performed in the same way as in the whole numbers. We first divide the two numbers ignoring the decimal point and then place the decimal point in the quotient in the same position as in the dividend.
The rules to divide a decimal by a whole number are:
(i) Divide as in division of numbers ignoring the decimal point.
(ii) When you reach the tenths digit, place the decimal in the quotient.
Note:
When the number of digits in the dividend is less and the division is
not complete, keep adding zeroes at every step till the division is
complete as in example 1 and example 2.
1. Solve: 100.4 ÷ 25
100.4 ÷ 25
Therefore, 100.4 ÷ 25 = 4.016
2. Find 1.2 ÷ 25
1.2 ÷ 25
= (12/10) ÷ 25
= (12/10) ×(1/25)
= (12 × 1)/(10 × 25)
= 12/250
Alternative Method:
Therefore, 1.2 ÷ 25 = 0.048
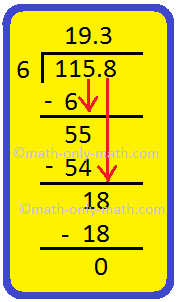
3. Divide 115.8 by 6
Hence, 115.8 ÷ 6 = 19.3
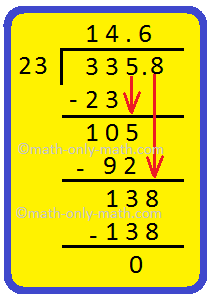
4. Divide 335.8 by 23
Hence, 335.8 ÷ 23 = 14.6
5. Divide: 191.5 ÷ 5
191.5 ÷ 5
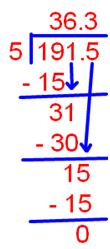
Therefore, 191.5 ÷ 5 = 36.3
This example shows that both dividend and quotient have decimal place i.e. 1.
6. Divide: 1.21 ÷ 11
First we will divide the decimal by the whole number ignoring decimal point.
Now put the decimal point in the quotient in such a way, that the decimal place in the quotient becomes equal to the decimal places in the dividend.
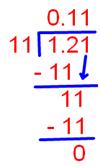
Therefore, 1.21 ÷ 11 = 0.11 (dividend has 2 decimal places, therefore
quotient also has 2 decimal places)
7. Divide: 798.3 ÷ 36
798.3 ÷ 36
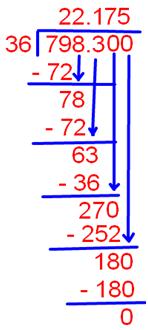
Therefore, 798.3 ÷ 36 = 22.175
8. Divide: 0.007 ÷ 14
0.007 ÷ 14
Therefore, 0.007 ÷ 14 = 0.0005 (dividend has 4 decimal places, therefore quotient also has 4 decimal places)
9. Divide: 24.66 ÷ 12
24.66 ÷ 12
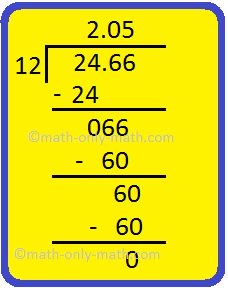
Therefore, 24.66 ÷ 12 = 2.05 (dividend has 2 decimal places, therefore quotient also has 2 decimal places)
10. Divide: 316.84 ÷ 8
316.84 ÷ 8
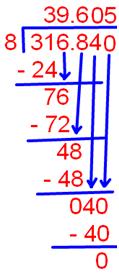
Therefore, 316.84 ÷ 8 = 39.605
11. Divide: 6.30 ÷ 7
6.30 ÷ 7
Therefore, 6.30 ÷ 7 = 0.90
(dividend has 2 decimal places, therefore
quotient also has 2 decimal places)
12. Divide: 1020.102 ÷ 51
1020.102 ÷ 51
Therefore, 1020.102 ÷ 51 = 20.002 (dividend has 3 decimal places, therefore quotient also has 3 decimal places)
You might like these
Fraction as Decimal | Converting Fractions | Fractions to Decimals Con
We will discuss how to express fraction as decimal. Let us consider some of the following examples on expressing a fraction as a decimal. 1. Convert \(\frac{4}{5}\) into a decimal.
Concept of Decimal | Decimal Point | Concept of Decimal System
We have already studied about fractions and now we will discuss here about the concept of decimal. Fractions can also be expressed as decimal Fractions.
Uses of Decimals | Decimals In Daily Life | Importance Of Decimals
We will learn uses decimals in every day. In daily life we use decimals while dealing with length, weight, money etc. Use of Decimals whole Dealing with Money: 100 paise = 1 rupee We know that one paise in one hundredth of a rupee.
Addition of Decimals | How to Add Decimals? | Adding Decimals|Addition
We will discuss here about the addition of decimals. Decimals are added in the same way as we add ordinary numbers. We arrange the digits in columns and then add as required. Let us consider some
Subtraction of Decimals | Subtracting Decimals | Decimal Subtraction
We will discuss here about the subtraction of decimals. Decimals are subtracted in the same way as we subtract ordinary numbers. We arrange the digits in columns
Equivalent Decimal Fractions | Like Decimal Fraction | Unlike Decimal
Equivalent decimal fractions are unlike fractions which are equal in value. Numbers obtained by inserting zeros after the extreme right digit in the decimal part of a decimal number are known as equivalent decimals.
Decimal as Fraction | Convert From a Decimal to a Fraction |Converting
We will discuss how to express decimal as fraction. Let us consider some of the following examples on expressing a decimal as a fraction. 1. Convert 2.12 into a fraction. Solution: 2.12
5th Grade Decimals Worksheet | Operations on Decimals | Comparing |Ans
In 5th Grade Decimals Worksheet contains various types of questions on operations on decimal numbers. The questions are based on formation of decimals, comparing decimals, Converting Fractions to Decimals, Addition of decimals, subtraction of decimals, multiplication of
Comparison of Decimal Fractions | Comparing Decimals Numbers | Decimal
While comparing natural numbers we first compare total number of digits in both the numbers and if they are equal then we compare the digit at the extreme left. If they also equal then we compare the next digit and so on. We follow the same pattern while comparing the
Expanded form of Decimal Fractions |How to Write a Decimal in Expanded
Decimal numbers can be expressed in expanded form using the place-value chart. In expanded form of decimal fractions we will learn how to read and write the decimal numbers. Note: When a decimal is missing either in the integral part or decimal part, substitute with 0.
Division of Decimal Fractions | Decimal Point | Division of Decimal
Division of a decimal number by 10, 100 or 1000 can be performed by moving the decimal point to the left by as many places as the number of zeroes in the divisor. The rules of division of decimal fractions by 10, 100, 1000 etc. are discussed here.
Addition of Decimal Fractions | Adding with Decimal Fractions|Decimals
Addition of decimal numbers are similar to addition of whole numbers. We convert them to like decimals and place the numbers vertically one below the other in such a way that the decimal point lies exactly on the vertical line. Add as usual as we learnt in the case of whole
Simplification in Decimals |PEMDAS Rule | Examples on Simplification
Simplification in decimals can be done with the help of PEMDAS Rule. From the above chart we can observe that first we have to work on "P or Parentheses" and then on "E or Exponents", then from
Worksheet on Decimal Word Problems |Prob Involving Order of Operations
Solve the questions given in the worksheet on decimal word problems at your own space. This worksheet provides a mixture of questions on decimals involving order of operations
Worksheet on Dividing Decimals | Huge Number of Decimal Division Prob
Practice the math questions given in the worksheet on dividing decimals. Divide the decimals to find the quotient, same like dividing whole numbers. This worksheet would be really good for the students to practice huge number of decimal division problems.
● Decimal.
- Tenth Place in Decimals
- Hundredths Place in Decimals
- Thousandths Place in Decimals
- Whole Numbers and Decimals
- Decimal Place Value Chart.
- Expanded form of Decimal Fractions
- Like Decimal Fractions.
- Unlike Decimal Fraction.
- Equivalent Decimal Fractions.
- Changing Unlike to Like Decimal Fractions.
- Ordering Decimals
- Comparison of Decimal Fractions.
- Conversion of a Decimal Fraction into a Fractional Number.
- Conversion of Fractions to Decimals Numbers.
- Addition of Decimal Fractions.
- Problems on Addition of Decimal Fractions
- Subtraction of Decimal Fractions.
- Problems on Subtraction of Decimal Fractions
- Multiplication of a Decimal Numbers.
- Multiplication of a Decimal by 10, 100, 1000
- Multiplication of a Decimal by a Decimal.
- Properties of Multiplication of Decimal Numbers.
- Problems on Multiplication of Decimal Fractions
- Division of a Decimal by a Whole Number.
- Division of Decimal Fractions
- Division of Decimal Fractions by Multiples.
- Division of a Decimal by a Decimal.
- Division of a whole number by a Decimal.
- Properties of Division of Decimal Numbers
- Problems on Division of Decimal Fractions
- Conversion of fraction to Decimal Fraction.
- Simplification in Decimals.
- Word Problems on Decimal.
5th Grade Math Problems
From Division of a Decimal by a whole number to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.