Equivalent Decimal Fractions

Equivalent decimal fractions are unlike fractions which are equal in value.

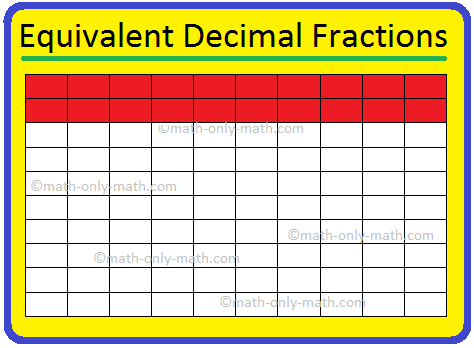
Let us take a plane sheet which represents one whole. Now, we divide the sheet into 10 equal parts. 

The colored part in the above figure represents two-tenths of the whole or 0.2.

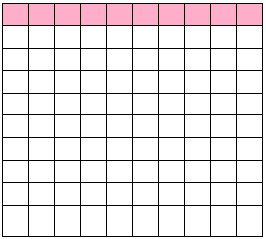
We now further divide the part into 10 equal parts. There are now 100 equal parts.

The colored part in figure B represents the fraction \(\frac{20}{100}\) or 0.02. Same way, if we divide further there will be 1000 equal parts and the colored part will represent \(\frac{200}{1000}\) or 0.200. The decimals 0.2, 0.20 and 0.200 are equivalent decimals. So, placing any number of zeroes to the right of the decimal part does not change its value.

Look at the figures:

Shaded portion indicates \(\frac{1}{10}\) = 0.1	Shaded portion indicates \(\frac{10}{100}\) = 0.10

Both the fractions indicate the same shaded portions.

Therefore, we have 0.10 = 0.1

Similarly 0.20 = 0.2;          0.30 = 0.3

Let us consider the following examples:

(i) 0.4, 0.40, 0.400, 0.4000

Each of the above is equal to 0.4 or 4/10.


(ii) 1.9, 1.90, 1.900, 1.9000

Each of the above is equal to 1.9 or 19/10.


(iii) 10.14, 10.140, 10.1400, 10.14000

Each of the above is equal to 10.14 or 1014/100.

(iv) 0.94, 0.940, 0.9400, 0.94000

Each of the above is equal to 0.94 or 94/100.


(v) 9.1, 9.10, 9.100, 9.1000

Each of the above is equal to 9.1 or 91/10.


(vi) 60.49, 60.4900, 60.490

Each of the above is equal to 60.49 or 6049/100.


Similarly, we have

0.300 = 0.30 = 0.3

0.700 = 0.70 = 0.7

0.200 = 0.20 = 0.2

Thus, by adding any number of zeros after the extreme right digit in the decimal part of a decimal number does not change the value of the number.

Numbers obtained by inserting zeros after the extreme right digit in the decimal part of a decimal number are known as equivalent decimals.

Hence, 0.75, 0.750, 0.7500 etc are equivalent decimals.

More Examples on Equivalent Decimal Fractions:

1. Is 0.90 = 0.9?

0.90 = \(\frac{90}{100}\)                        0.9 = \(\frac{9}{10}\)

\(\frac{90}{100}\) = \(\frac{9 × 10}{10 × 10}\)

That is, \(\frac{90}{100}\) and \(\frac{9}{10}\) are equivalent fractions.

Therefore, \(\frac{90}{100}\) = \(\frac{9}{10}\)

Hence 0.90 = 0.9

2. Is 0.900 = 0.9?

0.900 = \(\frac{900}{1000}\)                  0.9 = \(\frac{9}{10}\)

\(\frac{900}{1000}\) = \(\frac{9 × 100}{10 × 100}\)

That is, \(\frac{900}{1000}\) and \(\frac{9}{10}\) are equivalent fractions.

Therefore, \(\frac{900}{1000}\) = \(\frac{9}{10}\)

Hence 0.900 = 0.9

Similarly,          0.8 = 0.80 = 0.800 = 0.8000 and so on

                        0.7 = 0.70 = 0.700 = 0.7000 and so on

Adding one, two or three zeroes after the extreme right digit in the decimal part does not change the value of the fractional number.

For example:

0.25 = 0.250

0.46 = 0.4600

0.19 = 0.1900 and so on.

● Decimal.

Decimal Place Value Chart.

Expanded form of Decimal Fractions.

Like Decimal Fractions.

Unlike Decimal Fraction.

Equivalent Decimal Fractions.

Changing Unlike to Like Decimal Fractions.

Ordering Decimals

Comparison of Decimal Fractions.

Conversion of a Decimal Fraction into a Fractional Number.

Conversion of Fractions to Decimals Numbers.

Addition of Decimal Fractions.

Problems on Addition of Decimal Fractions

Subtraction of Decimal Fractions.

Problems on Subtraction of Decimal Fractions

Multiplication of a Decimal Numbers.

Multiplication of a Decimal by a Decimal.

Properties of Multiplication of Decimal Numbers.

Problems on Multiplication of Decimal Fractions

Division of a Decimal by a Whole Number.

Division of Decimal Fractions

Division of Decimal Fractions by Multiples.

Division of a Decimal by a Decimal.

Division of a whole number by a Decimal.

Properties of Division of Decimal Numbers

Problems on Division of Decimal Fractions

Conversion of fraction to Decimal Fraction.

Simplification in Decimals.

Word Problems on Decimal.

5th Grade Numbers Page

5th Grade Math Problems

From Equivalent Decimal Fractions to HOME PAGE