Multiplication of a Decimal by a Decimal

In multiplication of a decimal by a decimal number we will learn how to find the product of a decimal by another decimal.

To multiply a decimal number by a decimal number, we first multiply the two numbers ignoring the decimal points and then place the decimal point in the product in such a way that decimal places in the product is equal to the sum of the decimal places in the given numbers.

The rules to multiply a decimal by a decimal are:

(i) Remove the decimals of the two numbers and then take the two numbers as whole numbers and multiply.

(ii) In the product, place the decimal point after leaving digits equal to the total number of decimal places in both numbers.

(iii) Counting must always be done from the units place of the product.

Let us consider some of the following examples on multiplication of a decimal number by a decimal number.

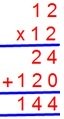
1. Find the product of 1.2 × 1.2

First we will perform the multiplication ignoring the decimal points in multiplicant and multiplier.

Since 12 × 12 = 144

Now place the decimal point in the product to give as many decimal places in the product as there are in the multiplicant and the multiplier together.

Therefore, 1.2 × 1.2 = 1.44

2. Find the product of 2.5 × 0.05

First we will perform the multiplication ignoring the decimal points.

Since 25 × 5 = 125

Now in the multiplicant and the multiplier there are three decimal places together, so the product also must contain three decimal places.

Therefore, 2.5 × 0.05 = 0.125

3. Multiply 128.16 by 2.5

Solution:

In 128.16, there are 2 decimal places after the decimal point and in 2.5, there are 1 decimal point after decimal point.

Therefore, total 2 + 1 = 3 decimal places

Now multiply, 12816 and 25

                       12816

                         × 25  

                       64080

                     256320  

                     320400  

Now place the decimal point to have three decimal places after the point.

Therefore,  128.16 × 2.5 = 320.400 i.e., 320.4

4. Multiply 9.17 by 0.5

Solution:

In 9.17, there are 2 decimal places after the decimal point and in 0.5, there are 1 decimal point after decimal point.

Therefore, total 2 + 1 = 3 decimal places

Now multiply, 917 and 05

                           917

                       ×     5  

                         4585

Now place the decimal point to have three decimal places after the point.

Therefore,  9.17 × 0.5 = 4.585

3. Find the product of 193.45 × 2.5

Perform the multiplication ignoring the decimal points in multiplicant and multiplier.

Since 19345 × 25 = 483625

Here the multiplicant contains two decimal places and multiplier contains one decimal place, so together the product must contain three decimal places.

Therefore, 193.45 × 2.5 = 483.625

4. Find the product of 26.452 × 2.1

Perform the multiplication ignoring the decimal points in multiplicant and multiplier.

Since 26452 × 21 = 555492

Here the multiplicant contains three decimal places and multiplier contains one decimal place, so together the product must contain four decimal places.

Therefore, 26.452 × 2.1 = 55.5492


5. Find the product of 96.41 × 1.02

Perform the multiplication ignoring the decimal points.

Since 9641 × 102 = 983382

Here the multiplicant contains two decimal places and multiplier contains two decimal places, so together the product must contain four decimal places.

Therefore, 96.41 × 1.02 = 98.3382


6. Find the product of 830.12 × 1.53

Perform the multiplication ignoring the decimal points.

Since 83012 × 153 = 12700836

Here the multiplicand and multiplier both contains two decimal places, so together the product must contain four decimal places.

Therefore, 830.12 × 1.53 = 1270.0836


7. Find the product of 183.31 × 3.11

Perform the multiplication ignoring the decimal points.

Since 18331 × 311 = 5700941

Here the multiplicant and multiplier both contains two decimal places, so together the product must contain four decimal places.

Therefore, 183.31 × 3.11 = 570.0941


8. Find the product of 900.09 × 0.99

Perform multiplication as usual ignoring the decimal points.

Since 90009 × 099 = 8910891

Here the multiplicant and multiplier both contains two decimal places, so together the product must contain four decimal places.

Therefore, 900.09 × 0.99 = 891.0891


9. Find the product of 432.01 × 4.2

Perform multiplication as usual ignoring the decimal points.

Since 43201 × 42 = 1814442

Now place the decimal point in the product to give as many decimal places in the multiplicant and the multiplier together.

Therefore, 432.01 × 4.2 = 1814.442


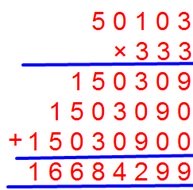
10. Find the product of 501.03 × 3.33

Perform multiplication as usual ignoring the decimal points.

Since 50103 × 333 = 16684299

Now place the decimal point in the product to give as many decimal places in the multiplicand and the multiplier together.

Therefore, 501.03 × 3.33 = 1668.4299

11. Multiply 813.9 by 2.62.

Solution:

Step I: Arrange the decimals in columns.

Step II: Multiply the numbers ignoring the decimal point.

            8139 × 2      =          16278

            8139 × 60    =         488340

            8139 × 200  =    + 1627800

                                         2132418

Step III: Count the number of decimal places in the multiplicand and multiplier and add them. Here, it is 1 + 2 = 3

Step IV: Count 3 digits from the extreme right of the product and insert the decimal point 2132418 → 2132.418

Multiply 813.9 by 2.62.

        813.9 → Decimal point after one digit from the right

        × 2.62 → Decimal point after two digits from the right

        16278

      488340

 + 1627800

   2132.418  → Decimal point after three (1 + 3) digits from the right

Answer: 2132.418

● Decimal.

• Tenth Place in Decimals
  
• Hundredths Place in Decimals
• Thousandths Place in Decimals
  
• Whole Numbers and Decimals
  
• Decimal Place Value Chart.
• Expanded form of Decimal Fractions
• Like Decimal Fractions.
• Unlike Decimal Fraction.
• Equivalent Decimal Fractions.
• Changing Unlike to Like Decimal Fractions.
• Ordering Decimals
• Comparison of Decimal Fractions.
• Conversion of a Decimal Fraction into a Fractional Number.
• Conversion of Fractions to Decimals Numbers.
• Addition of Decimal Fractions.
• Problems on Addition of Decimal Fractions
• Subtraction of Decimal Fractions.
• Problems on Subtraction of Decimal Fractions
• Multiplication of a Decimal Numbers.
• Multiplication of a Decimal by 10, 100, 1000
• Multiplication of a Decimal by a Decimal.
• Properties of Multiplication of Decimal Numbers.
• Problems on Multiplication of Decimal Fractions
• Division of a Decimal by a Whole Number.
• Division of Decimal Fractions
• Division of Decimal Fractions by Multiples.
• Division of a Decimal by a Decimal.
• Division of a whole number by a Decimal.
• Properties of Division of Decimal Numbers
• Problems on Division of Decimal Fractions
• Conversion of fraction to Decimal Fraction.
• Simplification in Decimals.
• Word Problems on Decimal.

5th Grade Numbers Page

5th Grade Math Problems

From Multiplication of a Decimal by a Decimal to HOME PAGE