Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Thousandths Place in Decimals
When we write a decimal number with three places, we are representing the thousandths place. Each part in the given figure represents one-thousandth of the whole.
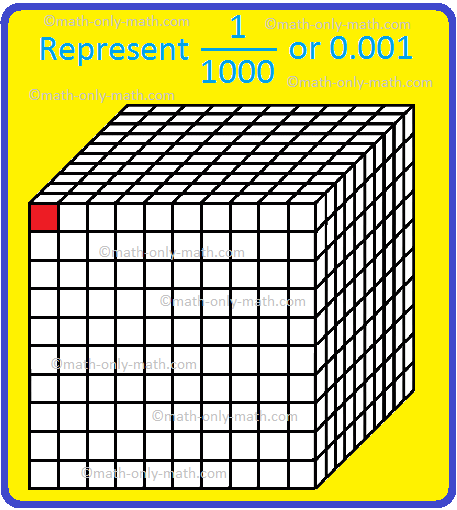
● Look at the given figure, which is divide into 100 equal parts, Each part is further divided into 10 equal parts, i.e., a square is divided into 1000 parts and out of it, 1 part is shaded. We say \(\frac{1}{1000}\) part is shaded.
It is written as \(\frac{1}{1000}\). In the decimal form it is written as 0.001. It is read as 'zero point zero zero one' or 'one thousandth'.
● If we take 9 parts out of 1000 equal parts of an object, then 9 parts make 9/1000 of the whole and it is written as 0.009
● Let us represent \(\frac{125}{1000}\).
In the given figure 125 parts of 1000 equal parts are colored. We write this as 0.125 in decimal form, where 1 represents 1 tenths, 2 represents 2 hundredths and 5 represents 5 thousandths. So, in the place-value chart 1 is written in the tenths column, 2 is written in the hundredth column and 5 is written in the thousandth column.
Similarly, we write We can also write, \(\frac{47}{1000}\), \(\frac{187}{1000}\), \(\frac{897}{1000}\) as 0.047, 0.187 and 0.897 respectively.
We can also write, \(\frac{4653}{1000}\) = 4.653, \(\frac{57025}{1000}\) = 57.025 and so on.
From the above discussion, we observe that a fraction in the form \(\frac{\textrm{number}}}{1000}\) is written as a decimal obtained by putting decimal point to the left of three right-most digits. If the number is short of digits, we insert zeros to the left of the number.
Decimal Places
From Thousandths Place in Decimals to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.