Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Converting Fractions to Decimals
In converting fractions to decimals, we know that decimals are fractions with denominators 10, 100, 1000 etc. In order to convert other fractions into decimals, we follow the following steps:
Step I: Convert the fraction into an equivalent fraction with denominator 10 or 100 or 1000 if it is not so.
Step II: Take the given fraction’s numerator. Then mark the decimal point after one place or two places or three places from right towards left if the given fraction’s denominator is 10 or 100 or 1000 respectively.
Note that; insert zeroes at the left of the numerator if the numerator has fewer digits.
● To convert a fraction having 10 in the denominator, we put the decimal point one place left of the first digit in the numerator.
For example:
(i) \(\frac{6}{10}\) = .6 or 0.6
(ii) \(\frac{16}{10}\) = 1.6
(iii) \(\frac{116}{10}\) = 11.6
(iv) \(\frac{1116}{10}\) = 111.6
● To convert a fraction having 100 in the denominator, we put the decimal point two places left of the first digit in the numerator.
For example:
(i) \(\frac{7}{100}\) = 0.07
(ii) \(\frac{77}{100}\) = 0.77
(iii) \(\frac{777}{100}\) = 7.77
(iv) \(\frac{7777}{100}\) = 77.77
● To convert a fraction having 1000 in the denominator, we put the decimal point three places left of the first digit in the numerator.
For example:
(i) \(\frac{9}{1000}\) = 0.009
(ii) \(\frac{99}{1000}\) = 0.099
(iii) \(\frac{999}{1000}\) = 0.999
(iv) \(\frac{9999}{1000}\) = 9.999
The problem will help us to
understand how to convert fraction into decimal.
In \(\frac{351}{100}\) we will change the fraction to decimal.
First write the numerator and then divide the numerator by denominator and complete the division.
Put the decimal point such that the number of digits in the decimal part is the same as the number of zeros in the denominator.
Let us check the division of decimal by showing a complete step by step decimal divide.
We know that when the number obtained by dividing by the denominator is the decimal form of the fraction.
There can be two situations in converting fractions to decimals:
• When division stops after a certain number of steps as the remainder becomes zero.
• When division continues as there is a remainder after every step.
Here, we will discuss when the division is complete.
Explanation on the method using a step-by-step example:
• Divide the numerator by denominator and complete the division.
• If a non-zero remainder is left, then put the decimal point in the dividend and the quotient.
• Now, put zero to the right of dividend and to the right of remainder.
• Divide as in case of whole number by repeating the above process until the remainder becomes zero.
1. Convert \(\frac{233}{100}\) into decimal.
Solution:
2. Express each of the following as decimals.
(i) \(\frac{15}{2}\)
Solution:
\(\frac{15}{2}\)
= \(\frac{15 × 5}{2 × 5}\)
= \(\frac{75}{10}\)
= 7.5
(Making the denominator 10 or higher power of 10)
(ii) \(\frac{19}{25}\)
Solution:
\(\frac{19}{25}\)
= \(\frac{19 × 4}{25 × 4}\)
= \(\frac{76}{100}\)
= 0.76
(iii) \(\frac{7}{50}\)
Solution:
\(\frac{7}{50}\) = \(\frac{7 × 2}{50 × 2}\) = \(\frac{14}{100}\) = 0.14
Note:
Conversion of fractions into decimals when denominator cannot be converted to 10 or higher power of 10 will be done in division of decimals.
Working Rules for Conversion of a Fractions into a Decimals:
To convert a common fraction into decimal number, we have to follow the following steps.
Step I: Change the given common fraction into an equivalent fraction whose denominator is 10 or 100 or 1000, etc.
Step II: Count the number of zeros in the denominator after 1.
Step III: In the numerator, start from the extreme right and move the decimal point to
Examples on Converting Fractions to Decimals:
1. Convert the following fractions into decimals.
(i) \(\frac{3}{4}\)
(ii) 5\(\frac{1}{2}\)
(iii) \(\frac{31}{125}\)
Solution:
(i) \(\frac{3}{4}\) = \(\frac{3 × 25}{4 × 25}\) = \(\frac{75}{100}\) = 0.75
(ii) 5\(\frac{1}{2}\) = \(\frac{11}{2}\) = \(\frac{11 × 5}{2 × 5}\) = \(\frac{55}{10}\) = 5.5
(iii) \(\frac{31}{125}\) = \(\frac{31 × 8}{125 × 8}\) = \(\frac{248}{1000}\) = 0.248
2. Convert 2\(\frac{7}{16}\) into a decimal.
Solution:
2\(\frac{7}{16}\) = \(\frac{2 × 16 + 7}{16}\) = \(\frac{32 + 7}{16}\) = \(\frac{39}{16}\)
Now, \(\frac{39}{16}\) = \(\frac{39 × 625}{16 × 625}\) = \(\frac{24375}{10000}\) = 2.4375
Thus, \(\frac{39}{16}\) = 2.4375
3. Express the following fractions as decimals:
(i) \(\frac{3}{10}\)
Solution:
Using the above method, we have
\(\frac{3}{10}\)
= 0.3
(ii) \(\frac{1479}{1000}\)
Solution:
\(\frac{1479}{1000}\)
= 1.479
(iii) 7\(\frac{1}{2}\)
Solution:
7\(\frac{1}{2}\)
= 7 + \(\frac{1}{2}\)
= 7 + \(\frac{5 × 1}{5 × 2}\)
= 7 + \(\frac{5}{10}\)
= 7 + 0.5
= 7.5
(iv) 9\(\frac{1}{4}\)
Solution:
9\(\frac{1}{4}\)
= 9 + \(\frac{1}{4}\)
= 9 + \(\frac{25 × 1}{25 × 4}\)
= 9 + \(\frac{25}{100}\)
= 9 + 0.25
= 9.25
(v) 12\(\frac{1}{8}\)
Solution:
12\(\frac{1}{8}\)
= 12 + \(\frac{1}{8}\)
= 12 + \(\frac{125 × 1}{125 × 8}\)
= 12 + \(\frac{125}{1000}\)
= 12 + 0.125
= 12.125
Converting a Common Fraction into a Decimal Fraction:
For converting a common fraction into a decimal fraction, we follow the division method. In this method, we take these steps.
Working Rules for Converting a Common Fraction into a Decimal Fraction:
Step I: Divide the numerators by the denominator till a non-zero remainder is obtained.
Step II: Put a decimal point in the dividend as well as in the quotient.
Step III: Put a zero on the right of the decimal point in the dividend as well as on the right of the remainder whenever required.
Step IV: Divide again just as we do in whole numbers.
Step V: Repeat step IV till the remainder is zero.
Examples on Converting a Common Fraction into a Decimal Fraction:
1. Convert into decimal.
(i) \(\frac{3}{4}\)
(ii) 4\(\frac{1}{4}\)
Solution:
(i) Divide the numerator 3 by the denominator 4.
Therefore, \(\frac{3}{4}\) = 0.75
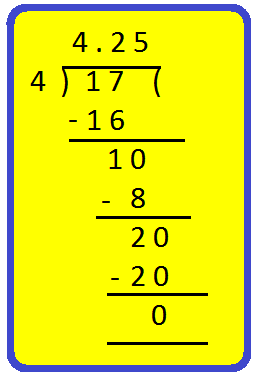
(ii) 4\(\frac{1}{4}\)
First convert into improper fraction
4\(\frac{1}{4}\) = \(\frac{4 × 4 + 1}{4}\) = \(\frac{17}{4}\)
Now, divide the numerator 17 by the denominator 4.
Therefore, 4\(\frac{1}{4}\) = 4.25
More Examples on Converting Fractions into Decimals:
Let us consider some examples
2. Convert the following into decimals
(i) 1/2
(ii) 5/8
(iii) 2/5
Solution:
As we know that decimal numbers are fractions with denominators as 10,100,1000, ... So, to convert a fraction into a decimal, multiply both the denominator and the numerator of the fraction with a number which can give you denominator as 10, 100, 1000 ....
(i) \(\frac{1}{2}\) = \(\frac{1 × 5}{2 × 5}\); (As 10 is the multiple of 2.)
= \(\frac{5}{10}\)
= 0.5
(ii) \(\frac{5}{8}\) = \(\frac{5 × 125}{8 × 125}\); (As 1000 is the multiple of 8.)
= \(\frac{625}{1000}\)
= 0.625
(iii) \(\frac{2}{5}\) = \(\frac{2 × 2}{5 × 2}\); (As 10 is the multiple of 5.)
= \(\frac{4}{10}\)
= 0.4
3. Convert the following into decimals
(i) 3\(\frac{3}{4}\)
(ii) 4\(\frac{2}{5}\)
Solution:
(i) 3\(\frac{3}{4}\) = \(\frac{3 × 4 + 3}{4}\)
= \(\frac{15}{4}\)
= \(\frac{15 × 25}{4 × 25}\)
= \(\frac{375}{100}\)
= 3.75
(ii) 4\(\frac{2}{5}\) = \(\frac{4 × 5 + 2}{5}\)
= \(\frac{22}{5}\)
= \(\frac{22 × 2}{5 × 2}\)
= \(\frac{44}{10}\)
= 4.4
Worksheet on Converting Fractions to Decimals:
1. Convert the following fractional numbers to decimal numbers:
(i) \(\frac{7}{10}\)
(ii) \(\frac{23}{100}\)
(iii) \(\frac{172}{100}\)
(iv) \(\frac{4905}{100}\)
(v) \(\frac{9}{1000}\)
(vi) \(\frac{84}{1000}\)
(i) \(\frac{672}{1000}\)
(i) \(\frac{4747}{1000}\)
Answers:
(i) 0.7
(ii) 0.23
(iii) 1.72
(iv) 49.05
(v) 0.009
(vi) 0.084
(i) 0.672
(i) 4.747
2. Express the following fractions as decimal numbers:
(i) \(\frac{2}{5}\)
(ii) \(\frac{9}{25}\)
(iii) \(\frac{8}{20}\)
(iv) \(\frac{22}{100}\)
(v) 2\(\frac{3}{4}\)
(vi) 9\(\frac{7}{25}\)
(vii) \(\frac{205}{125}\)
(viii) 16\(\frac{16}{40}\)
(ix) \(\frac{5926}{1000}\)
Answer:
2. (i) 0.4
(ii) 0.36
(iii) 0.4
(iv) 0.22
(v) 2.75
(vi) 9.36
(vii) 1.64
(viii) 16.4
(ix) 5.926
3. Convert into decimals.
(i) \(\frac{4}{5}\)
(ii) \(\frac{3}{10}\)
(iii) \(\frac{19}{50}\)
(iv) 4\(\frac{3}{4}\)
(v) \(\frac{7}{25}\)
(vi) \(\frac{26}{50}\)
(vii) 7\(\frac{1}{4}\)
(viii) 6\(\frac{7}{20}\)
(ix) \(\frac{3}{4}\)
(x) \(\frac{27}{40}\)
(xi) 9\(\frac{1}{2}\)
(xii) 20\(\frac{21}{200}\)
(xiii) 1\(\frac{17}{20}\)
(xiv) 4\(\frac{9}{25}\)
(xv) 3\(\frac{1}{4}\)
(xvi) 17\(\frac{3}{5}\)
(xvii) 2\(\frac{13}{25}\)
(xviii) 3\(\frac{17}{25}\)
(xix) 3\(\frac{2}{5}\)
(xx) 1\(\frac{17}{20}\)
(xxi) 3\(\frac{1}{50}\)
(xxii) 1\(\frac{76}{100}\)
(xxiii) 7\(\frac{5}{8}\)
(xxiv) 12\(\frac{3}{4}\)
(xxv) 16\(\frac{3}{20}\)
(xxvi) 2\(\frac{3}{25}\)
(xxvii) 3\(\frac{7}{20}\)
(xxviii) 8\(\frac{5}{8}\)
(xxix) 3\(\frac{4}{5}\)
(xxx) 25\(\frac{1}{4}\)
Answer:
3. (i) 0.8
(ii) 0.3
(iii) 0.38
(iv) 4.75
(v) o.28
(vi) 0.52
(vii) 7.25
(viii) 6.35
(ix) 0.75
(x) 0.675
(xi) 9.5
(xii) 20.105
(xiii) 1.85
(xiv) 4.36
(xv) 3.25
(xvi) 17.6
(xvii) 2.25
(xviii) 3.68
(xix) 3.4
(xx) 1.85
(xxi) 3.02
(xxii) 1.76
(xxiii) 7.625
(xxiv) 12.75
(xxv) 16.15
(xxvi) 2.12
(xxvii) 3.35
(xxviii) 8.625
(xxix) 3.8
(xxx) 25.25
4. Convert into decimals.
(i) \(\frac{3}{8}\)
(ii) 2\(\frac{5}{8}\)
(iii) 3\(\frac{1}{4}\)
(iv) 7\(\frac{1}{2}\)
(v) 1\(\frac{7}{8}\)
(vi) 4\(\frac{3}{5}\)
(vii) 6\(\frac{1}{5}\)
(viii) 9\(\frac{3}{6}\)
Answer:
4. Convert into decimals.
(i) 0.375
(ii) 2.625
(iii) 3.25
(iv) 7.5
(v) 1.875
(vi) 4.6
(vii) 6.2
(viii) 9.5
● Related Concept
● Decimals
● Conversion of Unlike Decimals to Like Decimals
● Decimal and Fractional Expansion
● Converting Decimals to Fractions
● Converting Fractions to Decimals
● H.C.F. and L.C.M. of Decimals
● Repeating or Recurring Decimal
● BODMAS/PEMDAS Rules - Involving Decimals
● PEMDAS Rules - Involving Integers
● PEMDAS Rules - Involving Decimals
● BODMAS Rules - Involving Integers
● Conversion of Pure Recurring Decimal into Vulgar Fraction
● Conversion of Mixed Recurring Decimals into Vulgar Fractions
● Rounding Decimals to the Nearest Whole Number
● Rounding Decimals to the Nearest Tenths
● Rounding Decimals to the Nearest Hundredths
● Simplify Decimals Involving Addition and Subtraction Decimals
● Multiplying Decimal by a Decimal Number
● Multiplying Decimal by a Whole Number
● Dividing Decimal by a Whole Number
● Dividing Decimal by a Decimal Number
7th Grade Math Problems
From Converting Fractions to Decimals to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
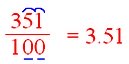
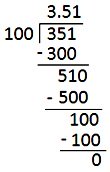
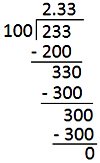




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.